[Planning][22.5][575] Planning with Diffusion for Flexible Behavior Synthesis

ad_official·2025년 1월 8일

diffusion planning

목록 보기

2/19

2022, 572회 인용
https://arxiv.org/pdf/2205.09991
https://github.com/jannerm/diffuser
- 933 stars

0. 바쁘신 분들을 위한 4줄 요약

model based RL은 환경만 학습하고, trajectory planning은 환경의 덜 학습된 부분으로 악용하여 궤적을 생성하는 단점이 있다. 이를 극복하기 위해 trajectory planning에 model-free RL 요소를 도입하였으나, 여전히 sparse-reward long term planning에 어려움을 겪는다.
data-driven diffusion based planning의 장점은 long-term planning 성능 + 학습 데이터 기반으로 새로운 (말이 되는) 궤적 생성 가능 + 한번 학습하면 다양한 길이의 trajectory 생성 가능 + 다양한 reward function을 test-time에 적용 가능
data-driven diffusion based planning의 단점은 느린 sampling 속도인데, 이를 warm-starting diffusion 기법으로 해결함. (직전에 만든 trajectory를 재활용하여, 거기에 조금만 노이즈를 줬다가 다시 denoising하는 방법임)
주로, Maze2D, Block Stacking, D4RL locomotion 등의 task에 수행했음.

1. Introduction

Model-based RL의 한계

Model-based RL

동적 모델(dynamics model) 학습
- 에이전트가 과거에 수집한 (상태 (s), 행동 (a), 다음 상태 (s')) 쌍들을 이용해, 환경의 동적 함수를 근사하는 모델 ( $f_\theta$ )를 학습합니다.
- 간단히 말하면 “( $\hat{s}_{t+1} = f_\theta(s_t, a_t)$ )” 형태의 1단계 예측(one-step prediction)이 가능해지는 것입니다.
- 학습된 동적 모델을 환경의 인과 구조(과거 상태·행동 → 현재 상태)와 동일하게 설계
플래너(trajectory optimizer)에 모델을 대입
- 학습된 모델 ( $f_\theta$ )를 고전적인 최적화 기법(예: iLQR, CEM, DDP 등)에 넣으면, 플래너는 다음과 같은 문제를 풉니다:
  $\max_{a_0, a_1, \dots, a_T} \sum_{t=0}^T r(s_t, a_t) \quad \text{subject to} \quad s_{t+1} = f_\theta(s_t, a_t).$
- 즉, “이 모델을 믿고, 주어진 보상 함수 (r)를 최대화하는 행동 시퀀스 ( $a_{0:T}$ )를 찾자”는 것입니다.
- 이렇게 하면, 실제 환경과 상호작용하기 전에 오프라인으로(혹은 시뮬레이션 상에서) 경로 최적화(trajectory optimization)를 수행할 수 있죠.

model-based RL의 장점

‘학습 기법을 가장 잘 활용할 수 있는 부분(=환경 동역학 추정, $s_{t+1} = f_\theta(s_t, a_t)$ )’에만 머신러닝을 적용한다는 점에 있다.
환경 동역학을 추정하는 것은 사실상 지도학습(supervised learning) 문제와 같기 때문에, 이미 성숙한(발전된) 지도학습 기법을 적극 활용할 수 있다.”
- 이런 점에서 “가장 성숙한(supervised learning) 기법”을 MBRL 내에 활용할 수 있다는 게 MBRL의 장점이라고 할 수 있습니다.

그런데 왜 문제가 생기는가?

학습된 모델 ( $f_\theta$ )가 진짜 환경(ground-truth dynamics)과 100% 일치하지는 않는다는 점이 핵심입니다.

모델은 경험해보지 못한 상태·행동 영역에서는 오차가 클 수 있습니다(‘모델이 모르는 영역’).
고전적 경로 최적화(예: iLQR, CEM 등)은 “주어진 모델 하에서” 보상을 최대화하려고 합니다.
- 즉, 모델이 틀릴 수 있는 구간을 “악용(exploit)”해, 모델 상에서는 보상이 엄청 커 보이지만 실제 환경에서 구현 불가능하거나 성능이 안 나오는 ‘가짜 해(adversarial trajectory)’를 제시할 수 있습니다.
이를 “Adversarial example”(적대적 예시)라고 부르기도 하는데, 즉 모델이 잘못된 부분을 플래너가 교묘하게 파고드는 상황입니다.

이런 현상 때문에 생기는 문제점

“학습된 모델을 가지고 최적화했는데도 실제 성능이 좋지 않은” 상황이 빈번히 발생합니다.
모델 예측이 틀려서 플래너가 허무맹랑한 궤적을 낼 때, 결국 다시 모델-프리(MF) 기법처럼 환경에서 직접 시행착오를 겪어야 할 수도 있습니다.
- 즉, 모델 기반이라고 해놓고, 실제로는 별도의 추가 탐색이나 모델-프리 학습을 많이 섞어 써야 할 수 있습니다.

해결책 1: 간단한 gradient-free 최적화 적용

‘랜덤 슈팅(random shooting)’ 이나 ‘크로스 엔트로피 방법(CEM)’ 같은 간단한 gradient-free 최적화를 주로 사용한다.
이는 앞서 말한 ‘모델이 부정확한 영역을 악용하여 이상한 계획을 내놓는 문제’ 등을 피하기 위해서다.”
부연 설명:
- 만약 iLQR처럼 모델의 미분 정보(gradient)를 예민하게 사용하는 최적화 알고리즘을 쓰면, 모델이 조금만 틀려도 매우 비현실적인 행동을 제안할 가능성이 커집니다(=모델 오차가 증폭됨).
- 반면 gradient-free 방식인 random shooting 또는 CEM은 “여러 액션 시퀀스를 무작위로 생성 → 모델로 시뮬레이션 → 높은 리턴을 주는 시퀀스를 선택 또는 재샘플링” 절차를 반복하므로, 모델이 틀린 부분이 있어도 어느 정도 완화시킬 수 있습니다.
- 즉, 모델을 세밀하게(미분 기반으로) 파고들지 않고, 상대적으로 단순화된 탐색을 하기 때문에 오차를 덜 ‘악용’하게 된다는 점에서, 실무적으로 선호되는 경우가 많습니다.

장점

모델 오차(에러)를 악용당할 가능성 감소
- Gradient-free 방식(random shooting, CEM)은 극단적으로 잘못된 그라디언트 계산을 사용하지 않으므로, 모델 오차에 덜 민감하고 상대적으로 견고(robust) 한 경향이 있음.
구현의 단순성
- Random shooting, CEM 등은 “액션 시퀀스를 무작위로 생성 → 예측 리턴(모델) 계산 → 우수한 시퀀스를 선택 or 업데이트”를 반복하는 방식으로 상대적으로 구현이 쉽고 직관적임.
비선형·불연속 동적 모델에도 적용 가능
- Gradient-based 방식은 미분 가능성(smoothness, continuity)을 가정하는 경우가 많음.
- Gradient-free 방식은 모델이 다소 비선형적이거나 불연속적이더라도 그대로 적용 가능.

단점

샘플 효율 및 계산 비용
- Gradient-free 방식은 여러 액션 시퀀스를 무작위로 생성하고 평가하는 과정을 많이 반복해야 하므로, 샘플링 비용(모델 호출 횟수)이 커질 수 있음.
- Gradient-based 방법은 계산이 더 복잡해도, 모델 도함수를 사용해 더 빠르게(더 적은 샘플로) 최적해에 수렴할 수 있는 잠재력이 있음.
탐색 품질
- Random shooting, CEM 같은 방식은 무작위 탐색에 기반하므로, 복잡한 고차원 액션 공간에서 로컬 옵티마에 빠지거나 적절한 분포 탐색에 실패할 가능성이 있음.
- Gradient-based 최적화는 잘 설계되면 고차원·복잡한 문제에서도 비교적 명확한 경로로 수렴하는 경우가 있음(물론 모델 오차 문제가 해결되었을 때).
하이퍼파라미터 의존성
- Gradient-free 최적화의 성공 여부는 종종 “샘플 개수”, “엘리트 비율(CEM)”, “액션 시퀀스 분포 초기화” 등에 크게 좌우됨.
- 적절한 하이퍼파라미터나 분포 업데이트 전략을 찾지 못하면 성능이 급격히 저하될 수 있음.

결론적으로

Gradient-free 최적화는 “간단하고, 모델 오차 악용이 덜하며, 미분 불가능한 모델에도 적용 가능”하다는 장점이 있으나, “샘플링 비용이 크고, 고차원 공간 탐색 효율이 떨어질 수 있다”는 단점이 있습니다.
반면 Gradient-based 최적화는 “빠른 수렴”이 가능하고 “고차원 문제에서도 효율적”이지만, “모델 오차에 아주 취약”하고 “미분 가능성”을 전제로 해야 하는 문제가 있습니다.

해결책 2: model-based에 model-free 요소를 도입

최신의 모델 기반 RL 알고리즘들은 ‘trajectory optimization’ 기법보다는, 오히려 value function나 policy gradient 등 모델-프리(MF) 알고리즘**의 요소들을 더 많이 활용하는 경향이 있다.”
이 접근은 보통 다음과 같은 흐름을 가집니다:

환경 동적 모델(approximate dynamics) 학습
모델로부터 샘플(rollout)을 생성하여 정책(Policy)이나 Q함수(Value function) 을 학습 (모델-프리 알고리즘 기법 활용)

예컨데,
Model Predictive Control(MPC) 대신, 모델로부터 만들어진 가상 데이터로 Off-Policy RL (SAC, TD3, DQN 등) 스타일의 업데이트를 진행하거나,
$\alpha$ -divergence 또는 policy optimization 기법을 모델에서 생성한 샘플에 적용할 수 있습니다.

실제 환경에서 이 정책(또는 Q함수로부터 유도된 정책)만을 사용해 행동

왜 이렇게 되었나?
1. 원래 MBRL 이론적으로는 ‘학습된 모델 + 경로 최적화 기법(iLQR, CEM 등)’을 쓰면 좋을 것 같았는데,
2. 실제로는 학습 모델이 정확하지 않은 영역을 최적화 기법이 ‘악용’하는 문제가 컸습니다(“adversarial example” 문제).
3. 그래서 대안적으로, 모델-프리 알고리즘에서 쓰는 가치 함수나 정책 학습 방식을 결합해서 문제를 풀어가는 방향(예: “MPCR”, “MBPO” 등)이 많이 등장한 것이죠.
4. 즉, 학습 모델이 있긴 해도, 최적의 정책을 찾는 과정에서는 결국 모델-프리 기반의 기법(‘policy gradient’, ‘value function’)에 많이 의존하게 되었다는 뜻입니다.

장점

상대적으로 안정적: 전통적인 모델-프리 학습 기법의 많은 성공 사례와 이론적 근거가 있어서, 모델 오차가 있더라도 어느 정도 Q함수(가치 함수)나 정책 네트워크가 이를 보완할 수 있습니다.

단점

모델-프리 부분이 장기 플래닝(trajectory-level 계획)을 온전히 잘 해낸다고 보장하기 어렵습니다.
- 가치 함수나 정책은 특정 상태 인근에서의 “로컬” 정보로 업데이트를 진행하기 때문에,
- 장기적 희박 보상(sparse reward) 문제에서 “크게 개선된 해결책”이 될지는 확실치 않습니다.
학습된 모델이 있음에도, policy gradient 또는 value function 업데이트가 결국 ‘근시안적(myopic)’으로 작동하기 쉽습니다.
계획(Planning) 자체의 해석 가능성이 낮아질 수 있습니다. (정책이나 Q함수가 “왜 그렇게 결정하는지”를 명시적으로 보긴 어려움)

논문의 해결책: Planing with Diffusion

data driven trajectory optimization
기존의 모델 기반 강화학습(MBRL)에서, 플래너는 모델 내부 구조를 전혀 알지 못하고, 모델은 플래너가 어떤 방식으로 최적화를 진행할지 전혀 고려하지 않습니다.
제 환경에서 계획이 실패해도 모델과 플래너 모두 서로에게 책임을 돌릴 뿐, 해결이 어렵습니다.

모델과 플래너를 한 몸으로 설계하자!

논문에서 말하는 핵심은 “모델을 학습하는 시점부터, 플래닝(trajectory optimization)의 목표와 제약 조건을 고려하자”는 아이디어입니다.
- 여기서 모델은 “( $\hat{s}_{t+1} = f_\theta(s_t, a_t)$ )” 가 아닙니다.
- 예측 정확도 “( $\hat{s}_{t+1} = f_\theta(s_t, a_t)$ )”를 암시적으로 좋게 하면서도, 모델이 만들어내는 궤적(플랜)도 점점 개선되고, 기존의 shooting 알고리즘에서 흔히 나타나는 ‘근시안적 실패’를 회피할 수 있도록 해야 한다.”
다시 말해, 모델 자체가 ‘미래 궤적을 예측하는 역할’에 더해 ‘목적을 달성하기 위한 궤적을 생성(=플래닝)’하는 역할까지 수행하도록 설계한다는 뜻이죠.
- 이를 위해서는, 우리는 state dynamics 뿐만 아니라, action distribtuion도 매우 중요해진다.
- 그리고 single-step error보다는 long-horizon 정확도가 더 중요해진다.
- 그리고 보상함수의 종류에도 무관하도록 설계하자.
  예를 들어,
Diffusion 모델을 통해 “(시작 상태, 목표 상태, 또는 보상 함수) 등 플래닝에 필요한 정보를 입력으로 주었을 때, 물리적으로 타당하면서도 원하는 목표에 부합하는 미래 궤적 $\tau$ 를 생성한다.”

이렇게 되면,
1. 학습된 모델(생성 모델) 내부가 이미 “플래닝” 개념을 품고 있기 때문에, “샘플링” 자체가 곧 “계획을 세우는 일”이 됩니다.
2. 플래너(=모델)가 스스로 학습 과정에서 “정상적인 궤적만 생성하도록” 훈련되므로, 따로 모델 오차를 악용할 틈이 줄어듭니다.
3. 테스트 시점에 목표나 보상을 새로 주었을 때, 모델이 그 정보를 받아 “조건부 궤적(conditional trajectory)”을 생성해주는 식이므로, 재학습 없이도 다양한 목표/보상에 바로 대응할 수 있습니다(유연성).

표준적 model based planning은 autoregressive 하게 동작하지만, diffuser은 한꺼번에 all timestep을 예측합니다.

장점

모델-플래너 통합:
- 모델과 플래너가 분리되지 않고 하나의 확률적 생성기으로 묶여 있어서, 모델 오차를 악용하는 전통적 최적화 문제(Adversarial Example)가 비교적 적습니다.
특히 long-horizion 추론과 test-time 유연성이 요구되는 offline control setting에서 효과적임
나머지 장점은 다음 장에서 설명

단점

샘플링(denoising) 비용:
- Diffusion 특성상, 매 타임스텝 실행 시마다(혹은 재계획 시마다) 여러 번의 denoising step이 필요할 수 있습니다 → 온라인 구현 시 계산량이 클 수 있음.
- 다만, 논문에서도 warm-start 기법(이전 플랜을 부분적으로 노이즈 주입 후 재샘플링) 등을 통해 완화하는 방안을 제시했습니다.
Diffusion 모델이 “학습 데이터 분포 + 보상/조건” 범위 안에서만 유효하게 플랜을 생성할 텐데, 데이터 외부(out-of-distribution) 상태에서는 여전히 한계가 있을 수 있습니다.

3. Planning with Diffusion

DDPM의 학습 방식과 똑같음
분산은 학습하지 않고, 평균을 계산하기 위한 노이즈만 네트워크가 추정함
guidance는 어떻게 주는가?
- 위 식 (1)의
  - h: guidance
    - prior evidence (e.g. observation history)
    - desired outcome(e.g. goal to reach)
    - general function to optimize (e.g. reward/cost)
  - p: physically realistic trajectory를 생성하는데 도움

3.1. A generative model for trjactory planning

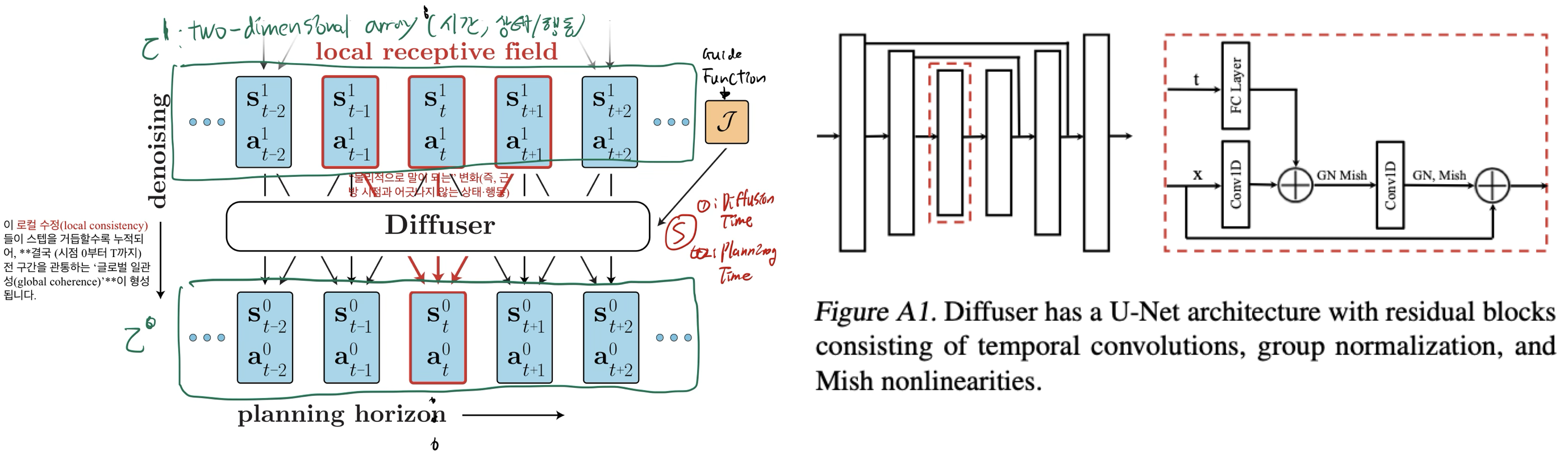
시간 축에 대해서 1D convolution을 반복

3.1.1. 각 실험과 state, action 정의

Maze2D & Multi2D
- State: 대체로 4차원 (x, y, vx, vy)
- Action: 2차원 (이동 방향/속도 제어)
- Dataset: D4RL에서 제공되는 Maze2D 데이터 (undirected 탐색 궤적)
Block Stacking
- State / Action: 논문에 구체적 차원 명시X; 블록들(위치, 회전 등) + 로봇 매니퓰레이터 상태/행동을 포함하는 고차원 벡터로 추정
- Dataset: PDDLStream으로 생성한 10,000개 데모 (다양한 블록 쌓기/재배치 시나리오)
D4RL Locomotion (HalfCheetah, Hopper, Walker2d 등)
- State: 로봇 관절 각도·속도 등 (대략 11~17차원)
- Action: 로봇 토크/힘 제어 (3~6차원)
- Dataset: D4RL의 (random, medium, medium-expert 등) 다양한 품질의 오프라인 데이터
공통적 특징:
- Diffuser는 모든 실험에서 “(state, action) 쌍을 이어붙인 2D 배열(시간×특징)” 형태로 데이터를 받아 학습.
- 학습 후, inpainting(조건부 샘플링) 혹은 reward gradient guidance를 통해 “플래닝(trajectory generation)”을 수행.

3.1.2. 만약 자율주행 차 planning에 쓴다면?

state: 자차, 주변차량들, 차선 정보
action: 자차의 제어 값

3.2. RL as Guided Sampling

$p(O_{t}=1) = e^{r(s_t,a_t)}$
- trajectory에서, t step의 state가 optimal일 확률
$p(O_{t}=0) = 1-p(O_{t}=1)$

3.3. Goal-Conditioned RL as Inpainting

perturbation function h는 아래와 같이 정의된다. (direc-delta funtion)
$c_t$ 는 timestep t에서의 state constraint 이다.
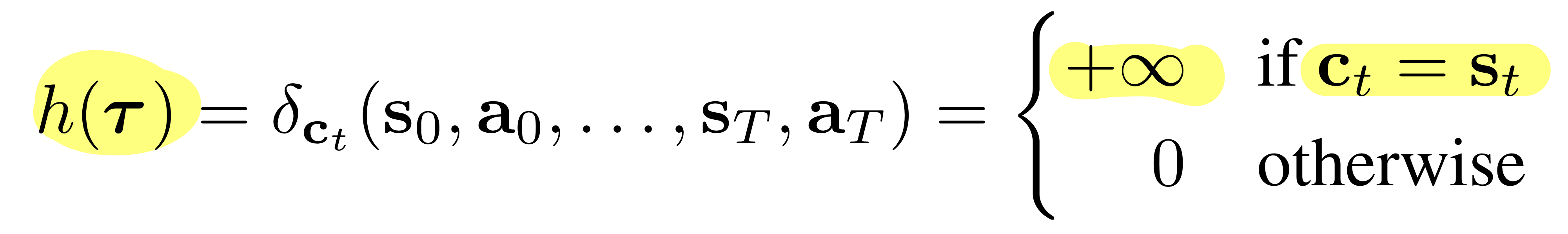
위 식을 식 (1)에 적용하면, 실질적으로는 아래와 같은 방식이 된다.
- 아래의 과정을 매 diffusion step마다 반복한다.
  - reverse process $p_{\theta}(\tau^{i-1}|\tau^{i})$ 을 구한 후,
  - $c_t$ 에 해당하는 부분을 대체한다.

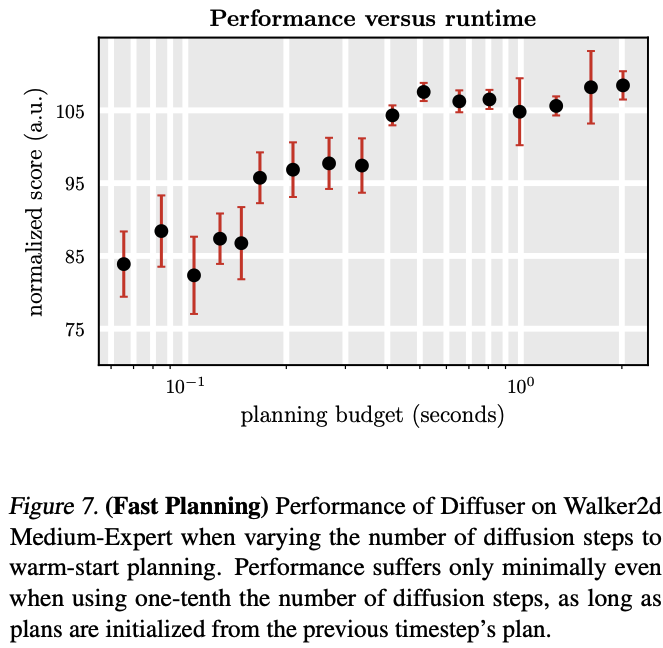
3.4. Warm-Starting Diffusion for Faster Planning

diffusion의 단점인 느린 sampling 속도 극복 방법?
- 직전에 생성했던 trajectory를 재활용하는 것! (warm-start planning)
구체적 방법
- 직전에 생성했던 trajectory( $τ^0$ )에 Forward diffusion을 “조금만” 수행해서, 예를 들어 k스텝 정도 노이즈를 주입하면 $τ^k$ 를 만든다.
- 이제 Reverse diffusion(denoising)을 “다시 $k$ 스텝” 수행해 $\tau^0$ 형태의 완성된 플랜을 얻습니다.
- 이때는 처음부터 전부(noisy $\tau^N$ 부터) 시작하는 게 아니라, $\tau^k$ 부터 역으로 되돌리므로 필요한 스텝 수가 적어 계산 비용 감소.
논문에서는 여러 실험((k=2)부터 (k=100)까지)으로 “얼마나 적은 denoising 스텝만 거쳐도 성능을 괜찮게 유지할 수 있는지”를 보여줍니다(그림 7).
결론적으로, denoising 스텝 수를 크게 줄여도(즉, 빠르게) 성능이 크게 떨어지지 않는다고 보고합니다.

Properties of Diffusion Planners

요약 정리

(a) Long-horizon:
- Shooting 알고리즘처럼 근시안적으로 탐색하지 않고, 전체 궤적을 확률적으로 생성함으로써 sparse reward 환경에서도 장기 계획이 가능해집니다.
- 따라서 “근시안적 failure”에 덜 취약합니다.
(b) Temporal compositionality (구성성):
- 모델 자체는 순차적(마코프) 예측 구조가 아니지만, denoising 과정에서 로컬(시간적으로 인접한 구간) 일관성을 점차 맞춤 → 최종적으로 전체 시퀀스가 자연스럽게 이어지는 결과를 얻습니다.
- 이 과정에서 학습 데이터에 있던 “부분 궤적(조각)”들을 이어 붙여, 새롭고 창의적인(하지만 물리적으로 말이 되는) 전체 플랜을 만들어낼 수 있습니다.
(c) Variable-length plans:
- 학습 때는 “horizon = 30” 스텝으로 해서, $(s_0, a_0, s_1, a_1, \dots, s_{30}, a_{30})$ 길이의 2D 텐서를 만들어 denoising했다면,
- 테스트 시점에는 “horizon = 50”으로 더 긴 텐서(노이즈)를 만들어 denoising할 수도 있습니다.
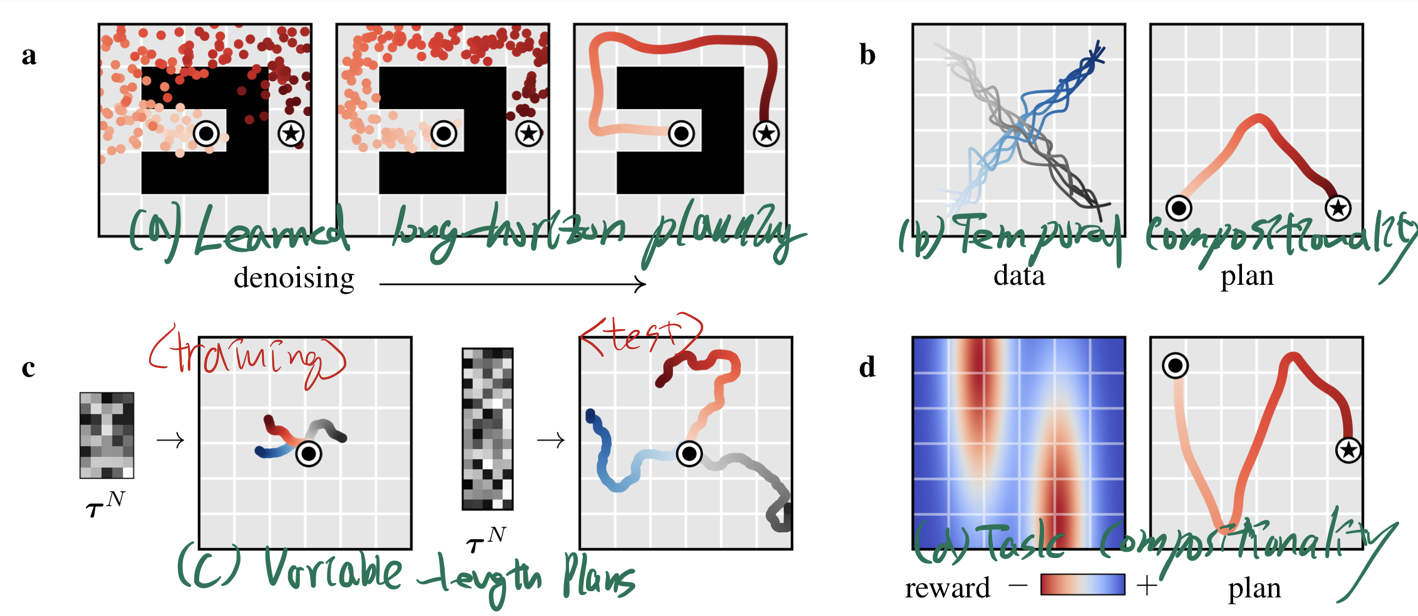
(d) task compositionality (구성성)
- diffuser은 새로운 reward function이나, Training 시 보지 못했던 새로운 task를 위한 Plan과도 잘 결합할 수 있습니다.

(a) Learned long-horizon planning

“Diffuser’s learned planning procedure does not suffer from the "myopic(근시안적) failure modes common to shooting algorithms" and is able to plan over long horizons with sparse reward.”

1. ‘Myopic failure modes’와 ‘shooting algorithms’

Shooting 알고리즘(shooting-based methods)은 흔히 모델 기반 강화학습(MBRL)에서 사용하는 기법으로, 예를 들어 CEM(Cross-Entropy Method)이나 random shooting 등이 대표적입니다.
- 이들은 “(학습된 또는 실제) 동적 모델 ( f )를 사용해 여러 개의 액션 시퀀스를 시도적으로 샘플링 → 각 시퀀스에 대해 rollout을 수행하여 누적 보상을 추정 → 그중 좋은 시퀀스를 골라서(또는 이를 기반으로) 새로운 시퀀스를 다시 샘플링 → 반복”하는 방식으로 작동합니다.
‘Myopic failure mode(근시안적 실패)’란,
- 이런 shooting 알고리즘이 짧은 구간(또는 특정 샘플)에만 집중하여 전역적으로는 최적인 해를 찾지 못하거나, 보상이 희박(sparse)한 상황에서 제대로 학습/탐색을 못 하는 문제를 말합니다.
- 예를 들어, 목표까지 수백 스텝이나 떨어져 있는데, 대부분의 시퀀스가 보상 0이라고 나오면(= sparse reward), shooting 알고리즘은 쉽게 탐색이 막히게 됩니다.

2. Diffuser가 긴 시간 범위(long-horizon)에서도 잘 동작하는 이유

Diffuser는 “샘플링 = 플래닝”이 되도록 학습된 확률적 생성 모델이므로, shooting 알고리즘처럼 매 스텝마다 무작위 액션 시퀀스를 뽑고 평가하는 과정을 반복하지 않습니다.
대신, 전체 궤적(trajectory)을 한꺼번에 생성(또는 denoising)하되, sparse reward나 목표 상태 같은 정보(예: gradient guidance)를 플랜에 직접 반영합니다.
그 결과, 장기적(수백 스텝)에 걸친 보상도 한 번의 생성(혹은 여러 단계의 denoising)으로 고려하게 되어,
- 마치 shooting 알고리즘이 여러 번 탐색해야 할 것을 한 번의 “diffusion sampling” 과정에서 처리할 수 있습니다.
따라서, “근시안적”으로만 최적화를 진행하다가 보상을 놓치는 실패 모드를 피하고, 긴 시간 범위에서도 목표 지점에 도달하는 계획을 세울 수 있게 됩니다.

(b) Temporal compositionality (시간적 구성성)

“Even though the model is not Markovian, it generates trajectories via iterated refinements to local consistency. As a result, it exhibits the types of generalization usually associated with Markovian models, with the ability to stitch(이어붙이다) together snippets of trajectories from the training data to generate novel plan.”

1. 모델이 ‘Markovian’하지 않음에도 불구하고...

Markovian 모델이란, 보통 “ $\;p(s_{t+1} | s_t)$ 만으로 미래를 결정”하는 형태처럼, “현재 시점만으로 다음 시점을 결정한다”고 보는 구조입니다(즉, 과거의 상태는 직접적 영향을 주지 않는다고 가정).
- Markovian 모델을 보통 일관성 성능이 좋습니다.
그런데 Diffuser는 한 시점씩 순차적으로 예측하기보다는, 전체 시퀀스를 동시에(혹은 병렬적으로) 다루면서 denoising을 수행합니다.
즉, 전통적인 (Markov) 1단계 예측 모델처럼 “ $s_t, a_t \rightarrow s_{t+1}$ ” 식의 인과(causality) 구조로만 동작하지 않는 비(非)마코프적 생성 모델입니다.

Diffuser는 denoising step마다, 해당 스텝에서 볼 수 있는 (시간적으로 근접한) 구간의 “물리적 일관성”을 높이는 방식으로 궤적을 점차 개선해 나갑니다.
- 예: (시간 (t) 전후 몇 스텝)에 대해서, 상태·행동이 자연스럽게 이어지도록 잡음(노이즈)을 줄이는 방식.
이렇게 “로컬(근방 시점)에서는 일관성을 강화”하고, 이를 여러 번 누적하다 보면, 전체 궤적이 전역적으로 잘 이어지는(글로벌 일관성) 형태가 됩니다.
이 과정을 거친 결과, “각 시점이 이전 시점과만 자연스럽게 이어지는” 것처럼 마코프적 특성이 나타납니다(실제로는 글로벌 정보를 간접적으로 반영).
- 즉, 비 마르코프 과정이지만, 마르코프 과정의 장점인 일관성 성능을 확보할 수 있습니다.

3. “Snippets of trajectories”를 이어 붙여 “새로운 플랜”을 만든다는 것

학습 데이터에서 “직진하는 경로”, “턴을 도는 경로” 등 다양한 ‘조각’(snippet)들이 있다고 해 봅시다.
Diffuser의 denoising 과정은 이 조각들을 재조합해서, “과거에 본 적 없는 새로운 궤적”을 자연스럽게 만들어낼 수 있습니다.
- 예: 과거엔 $s_0 \rightarrow \dots \rightarrow s_k$ 구간과 $s_k \rightarrow \dots \rightarrow s_T$ 구간이 별개로 존재했는데, Diffuser가 denoising 과정 중에 이 둘을 “잘 이어붙이면” $s_0 \rightarrow \dots \rightarrow s_k \rightarrow \dots \rightarrow s_T$ 형태의 새로운 경로가 탄생.
일반적으로, 1단계 예측 모델(마코프)에서도 “in-distribution” 구간끼리 이으면 새로운 궤적을 만들 수 있지만,
- Diffuser는 “로컬 일관성”을 바탕으로 전체를 동시에 다루어, 더 부드럽고 전역적으로 말이 되는 계획을 쉽게 구성해낼 수 있습니다.

(c) Variable-length plans

“Diffuser는 전체 궤적(trajectory)을 한꺼번에 다루는 모델이지만, ‘플래닝(계획)으로 삼을 수 있는 시간 길이(horizon)’가 모델 구조에 의해 고정되지 않는다. 학습 후에도 입력 노이즈의 차원만 바꾸면, 그 길이가 달라진 궤적을 샘플링할 수 있다.”

이를 이해하려면 Diffuser가 어떻게 ‘시간 차원’을 처리하는지 살펴봐야 합니다.

1. 일반적으로는 ‘모델 아키텍처가 길이를 고정’한다?

RNN(LSTM, GRU)이나 트랜스포머(Transformer) 같은 시계열 모델들은, 보통 (학습 시점에) 특정 길이 혹은 메모리 제한을 갖는 경우가 많습니다.
예컨대, “길이 (T)짜리 시퀀스를 학습”하면, 그 모델은 내부적으로 (T)에 맞춰 파라미터나 positional encoding 등을 세팅하기 때문에, 테스트 시점에 (T)가 크게 달라지면 제약이 생길 수 있습니다.

2. Diffuser의 “Fully Convolutional” 구조

Diffuser는 “이미지(2차원) 기반 U-Net”과 유사한 아이디어를 1차원 시계열(시간축)에 적용한, 소위 “완전 합성곱(fully convolutional)” 구조를 사용합니다.

즉, 가로 축(시간축)에 대해 “슬라이딩 윈도우” 형태의 1D 콘볼루션(Conv)을 적용하므로, 입력 길이가 늘어나거나 줄어들어도 합성곱 연산 자체에는 큰 문제가 없습니다.
(그림에서) 세로 방향은 상태·행동 차원, 가로 방향은 시간축이 되며, 네트워크는 시간축을 따라 합성곱 필터를 적용합니다.

이 말은 곧, “네트워크가 입력 시퀀스 길이(=플래닝 시점의 길이)에 대해 고정된 파라미터 개입 없이 유연하게 동작”한다는 뜻입니다.

“Fully convolutional” 구조에서는, 입력 차원이 달라져도(예: 10스텝짜리 vs. 20스텝짜리) 필터가 동일하게 작동하며, 출력도 그에 맞춰 늘어나거나 줄어듭니다.

3. “입력 노이즈”의 차원을 변경하면?

Diffuser에서 “ $\tau^N \sim \mathcal{N}(0, I)$ ” 형태로 초기 노이즈(가상의 궤적)를 샘플링할 때, 그 노이즈 벡터(또는 텐서)의 길이가 곧 “플래닝하려는 시퀀스 길이”를 결정합니다.

예: 학습 때는 “horizon = 30” 스텝으로 해서, $(s_0, a_0, s_1, a_1, \dots, s_{30}, a_{30})$ 길이의 2D 텐서를 만들어 denoising했다면,
테스트 시점에는 “horizon = 50”으로 더 긴 텐서(노이즈)를 만들어 denoising할 수도 있습니다.
네트워크 자체가 fully convolutional이므로, 30스텝 대신 50스텝 길이의 입력이 들어와도 (필터가 슬라이딩하면서) 문제없이 각 구간을 처리하고, 그 길이에 맞는 출력 궤적을 생성할 수 있게 됩니다.

따라서, 학습 과정에서 ‘시간축 길이’를 특정 값으로만 고정해 놓고 학습했더라도, 실제 샘플링(플래닝) 시점에는 노이즈 텐서의 크기를 바꾸어 더 짧거나 긴 궤적을 만들어낼 수 있는 것이죠.

이는 전형적인 RNN이나 Transformer에서 ‘position embedding’ 등을 고정해둔 방식과는 다른 큰 장점입니다.

ad_official