0. 원본 자료
- 논문: https://arxiv.org/pdf/2503.07565 (2025년 3월 10일 생 논문, DDIM 저자들이 쓴 논문)
- 서브-논문: https://arxiv.org/pdf/2503.07154
- 영문 블로그: https://lumalabs.ai/news/inductive-moment-matching
- github : https://github.com/lumalabs/imm
Abstract
- 기존 연구에서는 diffusion의 추론 속도를 높이기 위해 두 가지 방법을 사용했습니다.
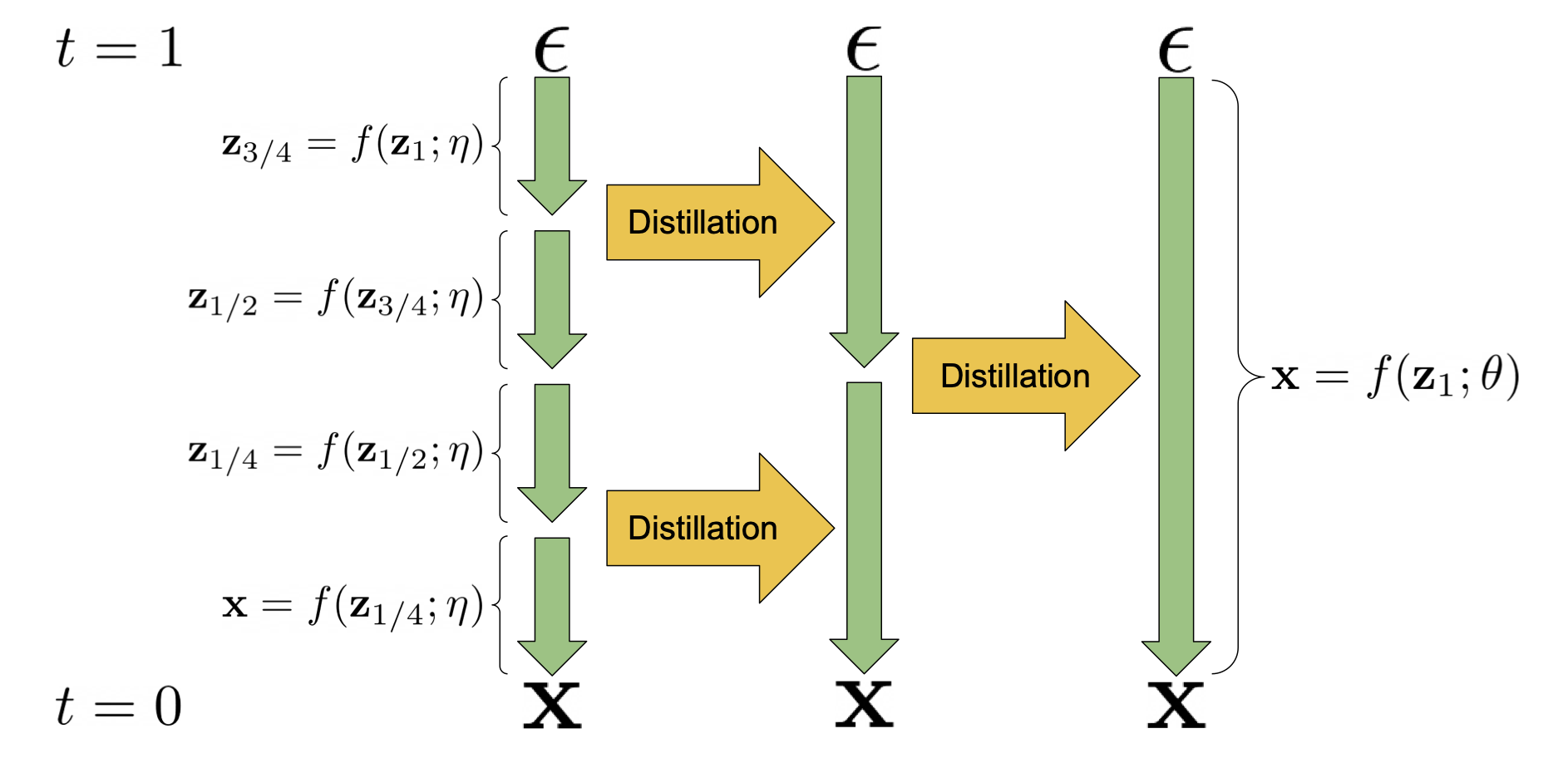
- 첫번째 방법: Distillation
- 목표: 원래 수백 단계의 생성 과정을 몇 단계(few-step)로 압축합니다.
- 문제점:
- 한 번에 큰 비선형 변화를 예측해야 하므로, 학습이 불안정해지고 에러가 누적될 위험
- 생성 분포와 실제 데이터 분포의 평균, 분산 등 모든 통계 정보를 맞춰야 하는데,
- 단계가 줄어들면 이 과정이 훨씬 민감해집니다.
- (각 단계가 담당하는 역할이 커지면서 목표 함수의 변화폭도 커짐)
- 결과적으로 매우 세밀한 하이퍼파라미터 튜닝이 필요
- 두번째 방법: Consistency Model (CM)
- 목표: 한 스텝으로 생성한 결과와 여러 스텝으로 생성한 결과가 비슷하도록 만듭니다.
- 한계점:
- CM은 주로
개별 샘플의 각 시점의 예측값 차이를 줄여 평균(첫 번째 모멘트)만 맞추게 됩니다. - 그래서 분산이나 왜도와 같은 고차원 통계 정보(나머지 모먼트 값들)는 충분히 반영되지 않을 수 있습니다.
- 이로 인해 CM은 학습 도중 불안정해짐
- CM은 주로
- IMM의 해결책:
- sammpling 을 1~4 step으로 줄여도, 성능은 오히려 더 좋음 (diffusion & flow matching 보다 )
- 기존 sampling을 빠르게 하기 위한 방법과 달리,
- 단일 모델, 단일 목적 함수로 한 번에 끝까지 학습하므로, 복잡한 2단계 훈련이나 teacher 모델 준비가 필요 없다
- 이론적으로 분포 수렴을 보장
- 특수한 하이퍼파라미터 설계에 의존하지 않고도 잘 동작하여, 모델 구조나 학습 설정을 유연하게 선택할 수 있다.
- 훈련 안정성이 높아 모델 규모나 학습 예산을 늘리는 대로 성능이 향상되는 긍정적인 스케일링 특징
- 구체적 동작 방식
생성된 데이터 분포와실제 데이터 분포의 분포 통계 모멘트들(평균,분산, 왜도, 첨도 등)를 일치시키는 Maximum Mean Discrepancy (MMD) 기반 목표함수를 사용하여 분포를 맞추는 것이 핵심- t (더 노이지)에서 s( 덜 노이지) 데이터 분포 를 유추하는게, 딥러닝 네트워크의 목표.
- 학습 초반에는, t와 s 차이를 적게 하다가, 갈수록 키우는 방법을 제안
- 아래 그림으로 느낌만 잡고, 넘어가도, 밑 글들에서 더 깊게 이해할 수 있습니다:)
- Consistency Model과 IMM의 관계
- 논문에서는 Consistency Model(CM)이 사실 IMM의 특수 케이스라는 점을 수학적으로 보입니다.
- 구체적으로, CM은 ‘단일 입자(single-particle)’ 그리고 ‘1차 모멘트(평균값만)’ 정도만 맞추는 버전이어서, 전체 분포를 폭넓게 커버하지 못합니다.
- 이런 제한이 CM을 훈련할 때 안정성이 떨어지는 이유 중 하나라고 설명하죠.
- 즉, IMM은 더 일반적인 분포 매칭 방식(모든 모멘트까지 고려)으로 안정적으로 학습하고, CM은 그중 일부(1차 모멘트)만 맞추는 경우라서 불안정성이 클 수 있다는 얘기예요.
- Consistency Model과 IMM의 관계
1. Introduction
1.1. stochastic interpolants & time-dependent marginal distributions
- 본 논문은 “stochastic interpolants(확률적 보간 함수)의 시간별 분포(time-dependent marginal distributions) 를 다룬다.”
stochastic interpolant(확률 보간 함수)이란?
- Albergo et al. (2023)이 개념 제안
- 아이디어: 데이터()와 노이즈() 사이를 확률적으로 “연결(interpolate)”하는 방식을 통칭.
- Albergo 등은 가 와 을 섞되, 그 섞임이 확률적 분포(가우시안)를 이룬다고 정의
- 즉, 분포로 정해짐. (가장 중요)
- 여기서 는 평균(보간의 중심), 는 해당 시점의 잡음 크기.
- 경계조건:
- 에서 (즉, 데이터)
- 에서 (즉, 노이즈)
- (초기·최종 시점엔 추가 잡음 없이 확정적)
time-dependent marginal distributions 란?
- 각 시간 (t)마다의 “진짜 분포”
- stochastic interpolant(확률 보간 함수) 로 인해 정의됨
IMM이 어떻게 활용하나?
- IMM은 노이즈 상태에서 데이터로 돌아오는 과정을 소수 단계(few-step)로 끝낼 수 있게 하려 합니다.
- 이를 위해, 임의의 시간 (t)에서, 모델이 목표 시간 (s)로 한 번에 점프(jump)할 수 있게 만든 뒤,
- 그 결과가 실제 (s) 시점 분포(time-dependent marginal distribution) 와 같아지도록(= “moment matching”) 훈련합니다.
- stochastic interpolant를 활용해 매 시점의 분포를 직접 정의해놓으면, 모델이 “현재 시간 분포→목표 시간 분포”를 맞추기 쉬워져요.
- 이렇게 하면 확산 모델처럼 모든 단계 하나하나를 거치지 않고도, 필요한 단계만큼만 써서 최종 이미지를 얻을 수 있어요.
1.2. construction by induction
수학적 귀납법(induction)이란?
- 작은(기본) 구간에서 참인 성질이 더 큰 구간에도 이어지도록 하여, 전체 구간에 대해 성립함을 보이는 논리.
- 예: (n=1)에 참인 것이
\(n\)에서 참이면 \(n+1\)에서도 참이라면, 모든 (n)에 대해 참이 되는 것과 같죠.
IMM에서의 ‘construction by induction’ (귀납적으로 구성함)
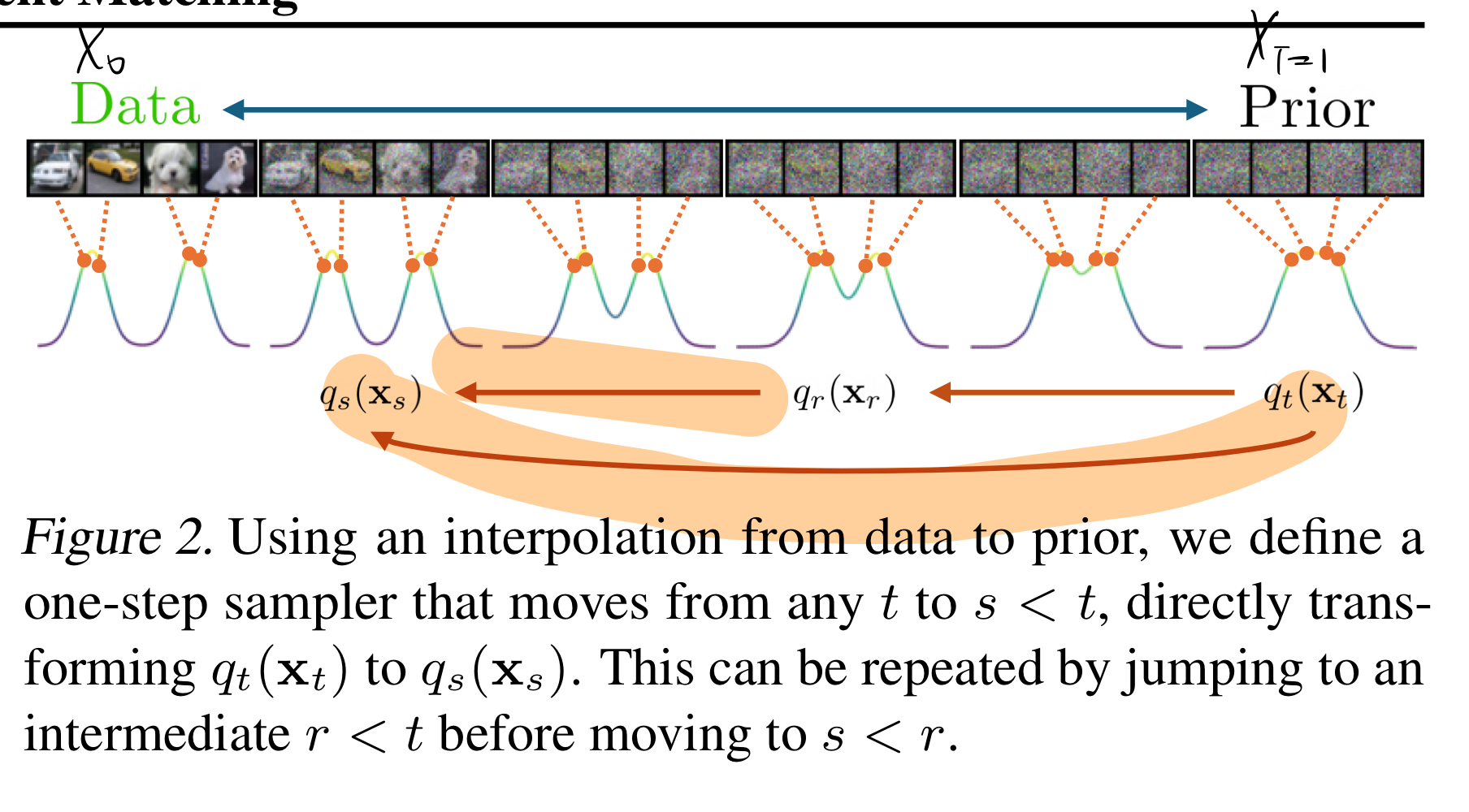
- 시간축을 data (0)부터 noise (1)까지 놓고, 예를 들어 (0 < s < r < t < 1) 구간을 잡아요. (아래 그림처럼)
- 시점 (r)에서 (s)로 가는 결과와, 시점 (t)에서 (s)로 가는 결과가 같은 분포를 내도록 학습해요. (즉, 둘의 차이를 최소화) (아래 그림의 주황색 형광팬)
- 시작점이 달라도, 결과는 같게
- 유식한 말로 self-consistency라고 부르기도 해요.
- 이렇게 작은 구간마다 “시작점 달라도 결과는 같다”는 조건을 계속 쌓아가면(시간 전 구간에 적용(귀납적으로 확장)하면),
- 결국 전체 구간(0~1)에서
노이즈 분포→데이터 분포변환 과정이 일관되게 맞춰지게 되죠.- s,r,t의 gap을 처음에는 작게 해서 학습하다가 -> 갈수록 커지게 함 -> 임의의 s,r,t에서 construction의 결과가 같아짐.
- 즉, construction by induction 을 수행하면, noise에서 data distrubtion으로의 변환과정에서의 수렴을 보장한다고 합니다.
- 결국 전체 구간(0~1)에서
2. Preliminaires
2.1 Diffusion, Flow Matching and Interpolants
- 요약하면,Flow Matching이나 -prediction Diffusion은,
- 각각 Stochastic Interpolants의 특수 케이스로 볼 수 있다.
- VP(Variance Preserving) Diffusion 모델과 Flow Matching은 둘 다
- “데이터↔노이즈” 사이를 시간에 따라 보간하고,
- “속도(=시간 변화율)”를 신경망으로 학습함으로써,
- 최종적으로 inference 시 “확률적 ODE”를 풀어 이미지를 생성한다는 원리를 공유
데이터 와 잡음 사이의 보간(Interpolation)
-
VP(Variance-Preserving) 확산 모델이나 Flow Matching(FM) 모델은, 원래 데이터()와 가우시안 잡음()을 시간 에 따라 섞은 를 만듭니다.
-
수식으로는
형태인데,
- 일 때(): 는 거의 “데이터 ”
- 일 때(): 는 거의 “순수 잡음 ”
-
VP 확산은 예를 들어
같은 식을 쓰고,
-
Flow Matching(FM)은
같이 더 단순한 선형 보간을 사용합니다.
속도 를 이용한 학습
- -prediction 확산이나 Flow Matching 둘 다, 가 시간에 따라 어떻게 변해야 하는지(= “속도” )를 뉴럴넷으로 예측하도록 합니다.
- 속도는 처럼 정의되며, 는 의 미분 같은 개념입니다.
- 즉, 신경망 = “가 더 미세한 시간 변화에서 어느 방향으로 움직여야 하는가?”를 예측하게 만듭니다.
확률적 ODE(확률 흐름 ODE, PF-ODE)로 샘플 생성
- 학습을 마친 뒤, 에 대한 미분방정식를 풀어서 데이터를 생성합니다.
- 초기값은 잡음 에서 시작(= 근처)해서, 점차 쪽(데이터)으로 이동하게 되죠.
- 이것이 확산 모델이나 Flow Matching 방식에서 실제 이미지를 뽑는 과정입니다.
왜 Stochastic Interpolants가 “diffusion & FM”을 통합한거야?
- Diffusion 모델도 데이터와 잡음 사이를 점진적으로 섞으면서,
- Flow Matching (FM)도 선형(혹은 간단한) 보간으로 데이터↔잡음을 연결합니다.
- Stochastic Interpolants는 이 둘을 일반화/통합한 개념으로,
- “데이터와 노이즈 사이의 경로를 확률적으로 설정하고, 그 경로를 학습한다”라는 시각을 제공합니다.
- [flow Matching] ,
- 완전히 정해진(랜덤 없이) 선형 보간이므로, 이때 은 Flow Matching(FM)에서 쓰는 속도와 동일.
- 따라서 학습/추론이 FM과 똑같이 됩니다.
- [Diffusion Model] 인 경우임
- 이때 stochastic interpolants를 쓰면, 사실상 -prediction Diffusion 형태로 돌아갑니다. (즉, 기존 확산 모델과 동일한 수식 구조)
Conditional Interpolant Velocity
-
는 시간에 따라 가 어떻게 변해야 하는지(=속도)를 나타냅니다.
-
식:
- 는 평균(보간 중심)이 에 따라 변하는 방향,
- 는 추가 잡음(무작위성)이 포함될 수 있는 방향을 의미해요.
-
뉴럴넷 로 를 예측하려면, 가 주어졌을 때의 평균적인 속도를 추정하면 됩니다.
2.2. Maximum Mean Discrepancy (MMD) ?
- Maximum Mean Discrepancy 이름의 유래 (재미로 보고 넘어가자)
- 두 분포를 가장 잘 구분해주는(=
"평균 차이(Mean Discrepancy)"를 최대화(Maximum) 해주는) Metric Function이다.
- 두 분포를 가장 잘 구분해주는(=
이걸 쓰는 목적: 쉬운 비유로 예시 들어보기
예) “클래스A, 클래스B 학생들의 시험점수 분포”
- 예시 상황
- 분포 (p): 클래스A 학생들 점수.
- 분포 (q): 클래스B 학생들 점수.
- 평균 점수(1차 모멘트)만 비교하면, “A반 평균 70, B반 평균 72, 비슷하다” 정도 알겠죠.
- 하지만 실제로는 A반은 분산이 매우 작고(점수가 고르게 60~80 사이), B반은 분산이 크고 양 극단(0점부터 100점까지)일 수도 있잖아요.
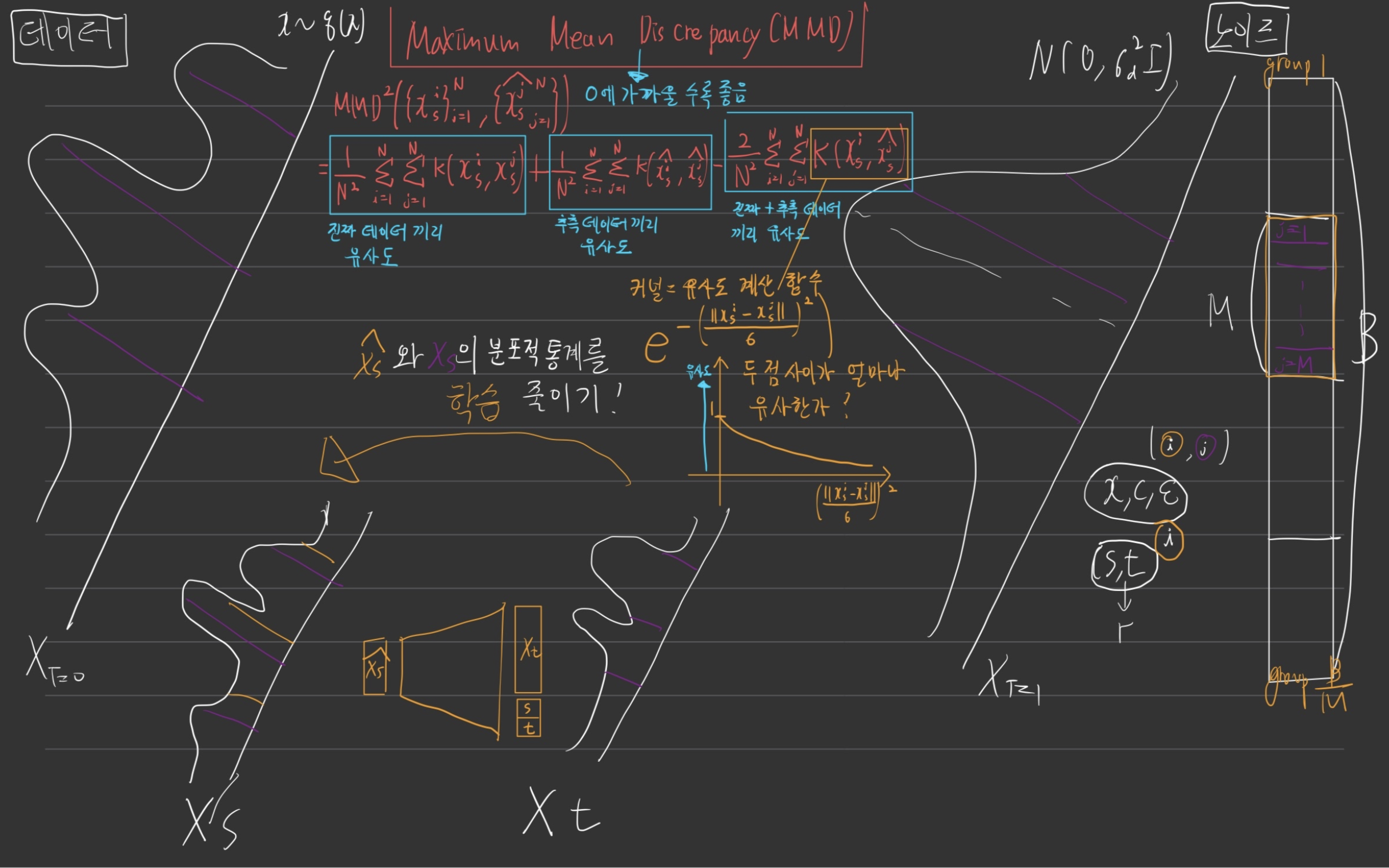
- MMD는 단순 “평균값”뿐 아니라, 분포 형태 전체(모멘트 전부 포함, 평균/분산/왜도/첨도)를 커널 함수을 통해 파악하므로,
- “두 점수 분포가 얼마나 다른가”를 훨씬 자세히 알 수 있게 됩니다.
- 아래 그림을 꼼꼼히 이해하려고 해보자.

RBF 커널의 특징
- 커널 = "데이터 간 유사도 측정" 함수
- 위 그림의 (주황색 글씨) 커널 수식인, ()이 RBF 커널의 하나의 예 라고 합니다.
- Radial Basis Function 이라고 함 (이름이 무슨 뜻인지는 모르겠음)
- RBF 커널을 쓰면, 그 “무한 차원 확장” 속에 분포의 다양한 모멘트 정보가 다 들어 있다고 해석할 수 있습니다.
- 결과적으로 MMD를 작게 만들려면, 분포의 1차 모멘트, 2차 모멘트, 3차 모멘트... 등등이 전부 유사해야(거의 같아야) 해요.
- 그래서 RBF 커널 기반 MMD가 분포 전반을 잘 구분할 수 있게 됩니다.
왜 MMD는 “유용”할까?
- 안정적 비교: MMD는 GAN처럼 “적대적 학습(미니맥스)” 없이도, 분포 사이 차이를 측정하고 줄여나갈 수 있어요.
- 분포 전반: 단순히 평균이나 분산만 맞추는 게 아니고, 더 풍부한 정보(모멘트 전부)를 포함해 “거의 모든” 차이를 발견할 수 있습니다.
- 간단한 구현: 실제 코딩 때는 샘플들끼리 커널 함수값을 계산해 평균 내면 되므로, 비교적 구현이 쉽습니다.
3. 본문: Inductive Moment Matching
- 제목 해석
귀납적인(Inductive) "평균, 분산, 왜도, 첨도 ..."(moment) 맞추기(Matching)!
- t에서의 distribution에서, s로의 distribution으로 변형하는
- implicit one-step model(one-step sampler)을 학습하는 것을 제안
- one-step model은
- t=1 -> t=0 으로 한번에 가는것도 가능하고,
- any t -> r -> s 로 recursive하게 가는 것도 가능하다. (s=0이 될 때까지)
- 이것은 bootstrapping(점진적 확장)을 통해, 모델이 생성한 sample로 부터, 모델이 스스로 학습할 수 있게 하는 것을 허용한다! (아래 글 읽다보면 이해됩니다.)
3.1. Model Construction via Interpolants
두괄식 정리
- 핵심 개념:
- stochastic Interpolant (복습): 시간 를 매개로 데이터 ↔ 노이즈 간에 확률적으로 섞이는 경로.(혹은 함수)
- time augmented interpolation
- Generalized Interpolant: “, 를 조건으로 시간 에 어떤 확률분포로 보간할지”를 더 확장된 형태로 논문에서 정의 (0()<s()<t()<1)
- stochastic Interpolant를 포함하는 더 넓은 개념
- Marginal-Preserving: Generalized Interpolant로 정의된 “ 시점 분포”가, 원래 우리가 의도한 와 똑같아지도록 유지 → “1-step sampler”를 써도 정확히 를 얻는다.
- stochastic Interpolant (복습): 시간 를 매개로 데이터 ↔ 노이즈 간에 확률적으로 섞이는 경로.(혹은 함수)
- 어떻게 쓰이나?
- 이렇게 정의해 놓으면, “주어진 샘플을 시간 로 바꾸는 과정”이 전부 하나의 알고리즘(혹은 함수)으로 정리됩니다.
- 즉, 를 넣으면 가 나오는 1-step 변환기, 이 변환기가 잘 만들어지면, 에서 시작해도 (실제 데이터) 상태로 한 번에 갈 수 있음을 보장.
논문의 전반적 목표: “한 단계(1-step) 변환”으로 분포를 옮기기
- 배경
- “시간 에서의 분포 ”를 “시간 에서의 분포 ”로 정확히 옮겨주는 특별한 보간(interpolation) 개념이 필요해요.
- 이걸 “marginal-preserving interpolant”(주변분포를 보존하는 보간)이라고 부릅니다.
- “시간 에서의 분포 ”를 “시간 에서의 분포 ”로 정확히 옮겨주는 특별한 보간(interpolation) 개념이 필요해요.
설명 시작: 식 (2)에서 말하는 “시간축 보간” 개념
- : 실제 데이터 분포에서 샘플
- : 사전 정의된 간단한 분포(보통 가우시안 잡음)에서 샘플.
- : “와 을 받아, ‘시간 ’ 상태의 샘플 를 어떻게 만드는가”를 정의하는 time augmented interpolation (
stochastic interpolant를 활용한)
- 즉, 는 “와 을 적절히 섞어서 나온 시점의 상태”라고 볼 수 있음.
- 그걸 전부 합치면( 적분), 결국 만 봤을 때(주변화), 어떤 분포가 되느냐가 라는 의미.
모든 데이터(x), 모든 노이즈() 사례를 다 종합하면, ‘t 시점의 사진 분포’()가 생겨납니다.
“1-step sampler”로 전환
- “ 분포를 갖고 있는 샘플을, 곧장 분포의 샘플로 바꿔 주는(‘transform’) 수 있는 모델을 만들자!”
- “그런 모델을 만들려면, 시점의 주변분포 와 일치하도록 하는 특별한 보간 과정이 필요하다.”
- 이 특별한 보간을 marginal-preserving interpolant라고 부르겠다는 것.
- 참고: 주변분포(marginal distribution)라 함은, “만 봤을 때의 분포를 의미”
- “preserving”은 “그걸 그대로 지켜낸다”는 뜻.
- 참고: 주변분포(marginal distribution)라 함은, “만 봤을 때의 분포를 의미”
식 (3) generalized interpolant 정의
- stochastic interpolant:
- generalized interpolant 은 s <- t 로 가는 과정
generalized interpolant:
Constraints:
즉, generalized interpolant는 “시간 의 샘플 와 원본 데이터 를 이어주는 가우시안 보간 과정”을 이런 방식으로 정의했을 때, 경계(시작/끝)에서는 확정값이고, 중간 시점에는 적절한 랜덤성을 줄 수 있게 함.
“When , it reduces to regular stochastic interpolants.”
- 이면, 우리가 흔히 아는 “완전 노이즈()와 데이터() 사이를 보간”하는 기본 확산(또는 Interpolant) 정의가 됩니다.
- 이때는 “, ” 같은 구조가 되어, ‘Stochastic Interpolant’(Albergo 등이 제안한 확률적 보간 모델)과 동일해진다는 말이에요.
- 즉 generalized interpolant이 더 큰 범주의 개념이고, stochastic interpolants는 그 안에 속하는 개념입니다.
Definition 1 (Marginal Preserving Interpolants)
두괄식 설명
- “Marginal-Preserving”이란, “시간 축 어디서 출발해도, ‘시점 ’에서의 결과물이 원래 와 완전히 같게끔 보간을 정의하는 것.”
- 이를 만족시키기 위해, 논문은 (4) (이론분포)와 (6) (모델분포)의 차이를 줄이는 목적함수(발산 최소화)를 제안하고, ( 수식은 아래에 나와요.)
- 그걸 통해 한 스텝/두 스텝/여러 스텝 샘플링이 모두 올바르게 진행되도록 유도하고자 하는 겁니다.
- 목표:
- “시간 ” 상태()에서 “시간 ” 상태()로 한 번에 이동하는 방식을 만들되, 가 반드시 “진짜 ”를 만족하도록 하자.
- 즉, 시점의 샘플을 어떤 보간 과정을 거쳐도, 시점 의 “정확한” 분포와 같아야 한다는 개념이 곧 “Marginal-Preserving Interpolant”.
Definition 1: Marginal-Preserving Interpolants
- 왼쪽의 는 “시점 ”에서의 참된(이론적) 분포.
- 오른쪽은 “에서 를 고려한 뒤, 를 만드는 보간”을 전부 합친(적분한) 것.
- 는 위에서 정의한 generalized interpolant 식 (3) -> 가우시안 분포
- 결과적으로, 이 등식은:
- “시점 에서 다양한 가 있을 수 있고, 그 가 어떤 원본 데이터 에서 왔을지도 모르는 상황을 다 고려했을 때,
- 최종적으로 생성되는 의 분포가 진짜 와 동일해야 한다”
- 즉, “Marginal(=시점 에서의 분포)이 보존된다”는 의미입니다.
와 사이의 관계: 식 (5)
- 아마 아래 식을 직접 구하긴 어려우니, 식 (6) 처럼 딥러닝 네트워크로 학습시키자는 의도 같음(내 생각임)
- “가 특정 에서 비롯된(조건부) 확률”을 구체적으로 나타낸 식.
- 분자: “에서 실제로 가 생기는 과정”, 분모: 전체 확률로 정규화.
- 요점: 가 어디서부터 왔는지(어떤 , 였는지)를 역추적하는 수식.
3. 식 (6): 모델 분포
- 이제 우리 모델이 정의한 과정을 녹여, 최종 가 어떤 분포를 갖는지 계산한 것.
- 로 시작해서,
- ""를 만들고(이는 라 부름),
- "와 " 정보를 이용해 시점 상태()를 만드는 과정().
- 는 위에서 정의한 generalized interpolant 식 (3) -> 가우시안 분포
- 그 전 과정을 몽땅 합쳐(적분) 얻은 모델 측 시점 분포가 .
- 이를 “Noisy model distribution at given ”라고 부름.
Multi-step Sampling (2-스텝 예시)
논문에서는 2스텝으로 샘플링하는 과정을 예시로 들어 설명합니다:
-
초기
- 시점 에서의 “진짜” 분포에서 샘플을 뽑았다고 가정. (실제로는 노이즈에서 만들어졌다고 볼 수도 있고, 관측된 값일 수도…)
-
(1단계)
- :
- 즉, “가 주어졌을 때, 모델이 를 하나 뽑는다.”
- 라고 이름 붙임.
- 그리고 :
- “와 로 시점 상태()를 만든다.”
- 이 부분이 generalized interpolation에 해당.
- :
-
(2단계)
- 시점 에서 최종적으로 (시점 0, 완전 데이터)에 도달하고 싶다면,
- 라는 식으로 또 한 번 샘플링.
- 이렇게 해서 로 가는 2단계 프로세스가 완성됨.
Marginal-preserving이 왜 중요할까?
- “의 분포가 실제 와 동일”해야, 2단계 과정에서 문제가 안 생깁니다.
- 즉, “중간 시점 분포가 올바르면, 거기서 또 한 번 샘플링해도 최종 0 시점(데이터)로 제대로 갈 수 있다”는 논리.
Equation (4) vs. (6)
결국 저자들은 “(4)에서 말하는 진짜 분포 ”와 “(6)에서 정의되는 모델 분포 ” 사이의 거리를 줄이고 싶어 합니다.
- 즉, 이 작은(가장 0에 가까운) 를 찾으면, “Marginal-Preserving”에 가까워진다는 뜻이죠.
정리 및 요약
- Definition 1에서 “Marginal-Preserving Interpolant”는, “어떤 시점 에서 로부터 시점 의 샘플 를 만들어도, 그 분포가 진짜 와 같아지도록 하는 보간”이라고 정의.
- 식 (5)는 가 어떤 에서 왔는지(역조건부)도 고려하는 공식.
- 식 (6)은 우리가 실제로 학습하는 모델 분포 정의. (거기엔 1-step sampler 가 들어감.)
- Multi-step(2-step) 샘플링으로 “중간 ”를 거쳐 최종 (데이터)까지 갈 수 있고, 그 중간에 Marginal-Preserving 속성이 중요함.
- 결과적으로, (4)와 (6) 간 차이를 발산으로 측정해 최소화하는 방식(예: MMD)을 쓰면, 변환을 잘 학습할 수 있다는 아이디어
Naive Objective
<복습>
한 문장으로 두괄식 요약
아래 식 (7) 같은 간단 손실로 시점 분포만 맞추면, Marginal-Preserving 식(4) 을 달성할 수 있다.
하지만 이건 경로(조건부)를 구체적으로 맞추는 것과는 달라서, 여러 가지 해법(결정적·확률적)이 공존한다.
- 이게 바로 논문이 말하는 “Naïve Objective”의 핵심 메시지입니다.
1. Naïve Objective(식 (7))의 아이디어
- 여기서 는 두 분포의 “차이(거리)”를 재는 방법(MMD, GAN loss 등).
- 은 “여러 시점 를 골라 평균을 낸다”는 뜻.
- 결론적으로, “모델이 만들어낸 시점 의 분포 가, 진짜 분포 와 최대한 가깝도록 손실을 줄이자.” 라는 의미입니다.
왜 “Naïve”(단순 접근)인가?
- 이 방식은 “최종 분포만” 보고 맞춥니다.
- 예: “시점 시점 ”로 갈 때, 어떤 경로를 거치든 상관없이, 결국 시점 결과가 와 똑같아지면 OK라는 식이죠.
- 내부에서 “”가 어떻게 되느냐는 깊이 신경 안 쓴다는 점에서 단순(naïve)하다는 겁니다.
하지만 “조건부 분포”까지 똑같아야 하는 건 아님
논문이 강조하는 부분:
"라고 해서
가 자동으로 성립하진 않는다."
- 즉, 최종 분포(마진 분포)가 일치한다고 해서,
- 개별 샘플 경로(조건부: 에서 어떤 를 거쳐 에 이르는지)까지 완전히 동일할 필요는 없다는 말.
그래서 최적해(해결책)가 여러 가지 존재
-
논문 말대로, 을 만족하려면, 마진 분포만 진짜와 같으면 되니까,
- ""나 ""를 어떻게 설계하든 괜찮습니다.
-
예:
- 결정적(Deterministic) 매핑("" 형태)이라 해도, 결과적인 시점 분포만 일치한다면 문제 없음.
- 또는 확률적(무작위) 매핑이라도, 최종 시점 분포만 진짜 와 똑같으면 OK.
-
이렇게 내부 구조(조건부 경로)를 구애받지 않으므로,
- 다양한 모델 설계가 가능,
- 즉, 해가 여러 가지 존재한다(“non-unique”).
3.2. Learning via Inductive Bootstrapping
- Inductive : 귀납적인
- Bootstrapping: 점진적 확장
- Learning via Inductive Bootstrapping: 귀납적인 점진적 확장 방식을 통해 학습하겠다.
왜 Naïve Objective(식 (7))가 학습하기 어렵나?
멀리 떨어진 시점 는 분포 차이가 크다
- 예: 이면 완전 노이즈, 이면 완전 데이터.
- 둘을 한 번에 매칭하려면, 모델이 “완전 노이즈 완전 데이터” 변환을 직접 학습해야 하고,
- 이는 분포 차이가 매우 커서 학습 난이도가 높아집니다(훈련이 불안정하거나, 수렴이 느리거나 등).
- 해결책의 실마리 -> 2. , 3. , 4.
2. 경계조건이 주는 이점:
- 논문에서 말하길, 인터폴런트(generailzed interpolant) 구조 덕분에 일 때 자동으로 가 성립한다고 해요 (Lemma 4 참고).
- 이 말은, “”(모델 파라미터)와 상관없이, 시점이 동일하면 분포를 맞추는 건 자동으로 해결된다는 겁니다.
3. 시점이 가까우면 “거의 맞춘다”
- 또한 가 에 가까우면 (가 작다면) 와 의 분포 차이가 작아서,
- 다시 말해, 시간이 아주 조금만 떨어져 있어도, 분포 변동 폭이 작으니 모델이 쉽고 안정적으로 학습할 수 있습니다.
4. 시점 와 가 가까울 때도, 분포가 비슷해진다
-
논문 문장:
“Interpolant enforces for any close to .”
-
즉, 시간 보다 조금 작은 에서 변환을 시도해도, 분포가 크게 달라지지 않는다(연속성).
-
따라서 “”에서 “”로만 살짝 이동해도 거의 같은 분포이므로, 가까운 구간끼리 맞추기가 쉬워집니다.
5. Inductive Learning Algorithm: 가까운 시점부터 차근차근
- 저자들은 이 성질(2, 3, 4 번 성질) 을 이용해, 부트스트래핑(bootstrapping, 점진적 확장) 방식을 제안합니다.
- 즉, “멀리 떨어진 시점끼리 매칭”을 시도하기보단, “시점 근처의 나, 또는 를 먼저 맞춰놓고, 그걸 단계적으로 확장하자”는 겁니다.
- 이 과정을 Inductive(귀납적)이라 부르는 이유:
- “시점이 거의 붙어있는 케이스부터 학습” → “조금 더 떨어진 케이스” → “더 멀리 떨어진 케이스” 식으로 점진적으로 확장.
6. 수열 와 함수
- 논문 설명에 따르면, 아래 방식대로 학습한다고 합니다.
- : 모델 파라미터를 학습하는 n번째 버전
- : 시점 에서 조금만 줄인(“finite decrement”) 시점. 즉, 이고 .
- 학습 방식:
- 즉, 이번 단계()에서 “” 구간을 학습할 때, 이전 단계()의 “” 구간 모델과 맞춰나간다는 전략.
7. 왜 이걸 “잘” 동작한다고 보나?
- 시점 → 분포 차이 작다
- 이미 로 를 잘 맞춰놨으니, 까지도 별 무리가 없다는 논리.
- 연속성(4) + 경계조건(3)
- 시점이 인접하면 분포가 크게 변하지 않는(“continuous around ”) 특성,
- 일 땐 자동 경계조건을 만족,
- 이런 점들이 부트스트랩(“점진적 확장”)을 가능케 하며, 훈련 난이도를 낮추죠.
General Objectives & Theorem 1
- :
- 두 분포 간 차이를 재는 지표(“Maximum Mean Discrepancy”).
- 간단히 말해, 분포가 같아지면 MMD=0이 되고, 다르면 양수가 됩니다.
- :
- 시점 쌍 에 대한 가중치 함수.
- 중요한 는 더 크게 가중을 줄 수도 있고, 덜 중요한 구간은 가중을 작게 줄 수도 있음(자유롭게 설정 가능).
Theorem 1
- “”: 우리가 부트스트래핑 스텝을 무한히 반복(또는 충분히 많이 반복)한다고 보면,
- 결과: 시점 에서 모델이 만들어내는 분포()가, 실제 와 완전히 같아진다 ().
해석
- 결국, “Inductive Bootstrapping + MMD 기반 목표(식 (8))”를 잘 구현하면, 무한 데이터·충분한 네트워크 용량이라는 이상적인 조건에서,
- “원하는 시점 모든 에 대해 진짜 분포를 정확히 재현”할 수 있음을 보장한다.
- 즉, “노이즈~데이터 사이 전체 구간”을 하나의 one-step sampler 로도 학습해낼 수 있다는 이론적 뒷받침입니다.
부록: B.3. Definition of Well-Conditioned r(s, t)
“Well-Conditioned”의 기본 개념
- Well-conditioned : 시점 에서 부드럽고(연속, 단조 증가), 역함수 존재하도록 조금 감소시켜서 를 만드는 함수.
- 부트스트래핑에서 “로 갔다가 다시 로 돌아오는 (또는 업데이트 시)” 때 역방향이 필요할 수 있어서, 역함수가 잘 정의되어야 한다
- “가 단조 증가” 형태면, 역함수도 쉽게 정의 가능.
식 (46)
- :
- 인 양의 함수.
- 즉, “시간 에서 얼마만큼 빼(or 줄이)면 ‘가까운 시점 이 되는지”를 정하는 함수라 보면 됩니다.
Constant Decrement in
-
정의
-
설정:
- 다소 혼동되는 표현이지만, 논문에서 말하는 건
“시간 전체 범위 을, 개로 나눠서 크기 정한다” 정도로 이해하면 됩니다. - 예: 이라면, “1을 1024분할”해서 한 번에 씩 빼는 식일 수 있죠.
- 다소 혼동되는 표현이지만, 논문에서 말하는 건
-
장점과 한계
- 장점: 아주 단순하고 구현하기 편함 (“그냥 ” 하면 끝).
- 한계: 확산 모델 특성상 “시간 ”와 실제 노이즈 비중()이 비선형 관계이므로,
한 번에 “0.1시간” 줄였다고 노이즈가 정확히 “균등하게” 줄어드는 건 아님. - 그래도 코드 측면에선 가장 쉽게 적용 가능하다는 의미로 소개.
부록: C.6. Mapping Function r(s, t)
Constant Decrement in
-
란?
- 흔히 확산 모델(Diffusion Model)에서 데이터 vs 노이즈 비중을 나타내는 변수들입니다.
- 는 “데이터 스케일”, 는 “노이즈 스케일”이라고 보시면 돼요.
- 예를 들어, 일 땐 , (데이터 100%, 노이즈 0%),
일 땐 , (노이즈 100%, 데이터 0%) 같은 식.
-
- 가 클수록 “노이즈가 훨씬 크다”(노이즈 많음),
- 작을수록 “데이터가 상대적으로 많다”(노이즈 적음)라는 의미가 됩니다.
-
에서 빼기
- 여기서 는 “-값을 입력받아 해당하는 시점 ”를 리턴해주는 역함수.
- 즉, “노이즈 비율()을 만큼 낮춘 뒤, 그걸 만족하는 시점 를 찾는다”는 개념
- 예: 만약 시점에서 (노이즈가 데이터의 10배)였다면, 라면
“노이즈가 8배 정도일 시점”을 로 삼는 식.
-
설정:
- , 이라고 가정
(대부분 확산 모델에서 가 최대 160배 가까이 커질 수 있다는 뜻). - 는 사이 숫자.
즉, 범위를 단계로 쪼개서 “한 번에 조금씩” 줄이는 방법입니다. - 왜 160? 저자들이 실험상 노이즈 최대치가 그 정도라고 파악한 예시로 보시면 됩니다.
- , 이라고 가정
-
논문이 “이 방식이 가장 좋다”는 이유
- “노이즈 비율”이라는 물리적·직관적 지표를 기반으로 시점을 줄이면,
학습이 더 매끄럽고 안정적이었다고 보고합니다. - 즉, 노이즈를 조금 줄인 상태 → 더 조금 줄인 상태 식으로 부트스트래핑하기가 편하다는 뜻이죠.
- “노이즈 비율”이라는 물리적·직관적 지표를 기반으로 시점을 줄이면,
4. Simplified Formulation and Practice
4.1. Algorithmic Considerations
Definition 2 (Self-Consistent Interpolants)
- 핵심 아이디어는 t에서 변환 시작할 때, “중간 시점 를 거치든, 안 거치든, 최종 분포가 같아야 한다”는 일종의 경로 일관성(path consistency) 조건을 정의하는 것
맥락: Marginal-Preserving과 Self-Consistency의 차이
- Marginal-Preserving:
- “시점 에서 시점 로 직접 보간해도, 결과 분포가 실제 와 일치한다”는 조건.
- Self-Consistency
- 시점 에서 직접 로 가든, 중간 시점 을 거쳐서 로 가든, 결과 분포가 동일해야 한다.
- 이 글에서 하고 싶은 이야기: Self-Consistency를 만족하면, 신기하게도 Marginal-Preserving도 자동으로 만족된다고 한 generalized interpolant !
2. 정의(Definition 2) 수식 (10)
- 복습: generalized interpolant 복습해보자.
-
Self-Consistency의 정의
-
왼쪽: “를 (직접) 에서 로 보간”했을 때의 분포. (generalized interpolant)
-
오른쪽: “먼저 로 를 하나 뽑고, 그다음 로 를 뽑는” 과정을 적분한 결과.
- 를 다양하게 뽑을 수 있으니, 전체 공간에 대해 적분.
직관
- 한 번에(직접) 해도,
- 나눠서(먼저 → 그다음 ) 해도,
- 최종적으로 가 나오는 분포가 동일해야 한다는 요구사항입니다.
4. (중요) Self-Consistency를 만족하면, Marginal Preserving을 자동으로 만족한다!!
- 논문에서 Lemma 5가 말하길, “Self-Consistent Marginal-Preserving”을 보장해 준다고 합니다.
- 즉,
자잘한 시점을 거치든 안 거치든 결과가 같다면, 결국 시점 에서의 분포가 늘 동일하게 되고,
그것이 우리가 의도한 와도 일치하도록 설계할 수 있다는 의미.
- 즉,
밑에서 다룰 내용: “DDIM”이나 “DDPM posterior”도 Self-Consistent 이고, 그러므로 "Marginal Preserving" 이기도 함.
lemma 6
- DDPM posterior도, 논문이 정의한 Self-Consistent 보간(interpolant)의 예시라는 것을 증명함
DDPM Posterior와 Self-Consistency의 맥락
- DDPM은, “시점 ”에 있는 샘플()을 “시점 ”로 만들 때 가우시안 형태의 식을 이용
- DDPM Posterior은 gaussian 형태
- Lemma 6에서 증명하려는 핵심은:
- 먼저 시점 에서 중간 시점 로 가는 식을 적용해 를 구한 뒤,
- 다시 로부터 시점 로 가는 식으로 를 구하더라도,
- 그 최종 결과가 “”로 직접 한 번에 갔을 때의 결과와 정확히 동일한 가우시안 분포가 됨을 보이겠다는 것
- 따라서 DDPM에서 사용하는 “posterior distribution”이,
- 중간 시점()으로 쪼개든 쪼개지 않든 동일한 최종 분포를 내보낸다는 것이 Self-Consistent의 정의와 일치.
- Lemma 6은 이 사실을 가우시안 전개를 통해 구체적으로 보여준 거고요.
마지막 언급: Diffusion GAN vs. Our Method
- 논문 말미에서, “Diffusion GAN 방식은 이 조건부 분포를 직접 학습하는 반면, 우리가 제시하는 방법은 마진 분포를 학습한다”는 언급이 나옵니다.
- 즉, Diffusion GAN은 “”라는 조건부 분포를 맞추려고 하고, 그게 유일한 해가 되지만,
- 여기서는 “분포 수준”에서 매칭하기 때문에, 내부 조건부 과정이 여러 형태가 될 수 있어 (즉, 해가 여러 개).
- 한마디로, “우리 방식(마진 매칭)은 해가 유연하게 많을 수 있다”는 코멘트로 끝납니다.
DDIM interpolant
1. DDIM이란?
- Denoising Diffusion Implicit Models은 기존 확산 모델(Diffusion Model)에서,
- 다단계로 샘플링해야 하는 비효율성을 줄이기 위해,
- ODE(상미분방정식) 기반으로 시점 에서 시점 로 한 번에 점프하는 해석 방식을 제안한 기법
- 쉽게 말해, “느리게 조금씩 잡음을 제거”하던 과정을, “기울기(ODE)만 잘 추적하면 적은 단계로도 가능”하게 만든 아이디어입니다.
2. 식 (11): DDIM은 결정론적 generalized interpolant
- 복습: generalized interpolant ?
- DDIM
- : 시점 0(원본 데이터) 쪽 정보를 나타내는 값.
- 실제론 (깨끗한 이미지를 추정한 값)으로 대체. 네트워크가 “현재 이면 원본 는 이런 식으로 복원”이라고 예측해준다고 보면 됩니다.
- / : 확산 모델에서 흔히 쓰이는 계수들로, “데이터 vs 노이즈” 비중을 각각 시간 에 대해 나타냄.
- 예: (시점 0이면 완전 데이터), (시점 1이면 완전 노이즈) 식으로 스케줄링.
- 식 (11)은 “와 를 적절히 섞어서 를 구한다”는 결정론적 레시피
3. DDIM 보간에서 란?
- generalized interpolant은 “시간 에서 로 갈 때, ‘평균(중심)’ + ‘잡음()’” 형태 (예: ).
- 그런데 DDIM은 잡음()이 없는 순수 결정론이므로, 로 표현합니다.
- 즉, 가 오직 식 (11)에 의해 딱 하나의 값으로 정해지므로, 확률분포 관점에서 델타() 분포로 적히는 겁니다 (즉, “다른 가능성 = 0, 이 값 = 100%”).
4. 왜 DDIM Interpolant가 Self-Consistent인가?
- Self-Consistent란, “”로 직접 가든, 중간에 시점 을 거쳐 로 가든, 결과가 동일한 분포를 이룬다는 조건입니다.
- DDIM 식 (11)을 한 번 더 적용(“중간 시점 에서 또 식 (11)”) 해보면,
- 최종 시점 결과가 한 번에 적용한 것과 똑같은 수식을 만족함을 확인할 수 있습니다.
- 논문 본문(부록 C.1)에서 이걸 수식으로 보여주는데, 한 번 더 DDIM을 안에 집어넣으면
라는 식이 성립해요.
- 이로써 “중간 분할 경로 = 직행 경로”, 결과가 동일 Self-Consistent임을 증명합니다.
5. 결정론적 보간 “Deterministic Minimizer” 가능
- 복습
- 논문에서 “Eq. (7)”이라 부르는 것은, 형태의 나이브 오브젝티브였는데, “최종 분포 vs. 실제 분포” 간 거리를 줄이는 작업이었습니다.
- DDIM처럼 결정론적 방식을 택하면, “조건부 분포() = 델타 분포”가 되고, 그걸 잘 학습하면 유일한 해(, “Deterministic Minimizer”)로 수렴할 수 있다는 뜻이에요.
- 반면, 논문이 제안하는 마진 매칭 방식(“IMM” 등)은, 내부 조건부 구조가 여러 형태여도(랜덤이건 결정론이건) 최종 분포만 맞추면 되므로, 해가 여러 개 있을 수 있다고 말합니다.
6. 결론
- DDIM은 시점 에서 로 가는 “결정론적 ODE 보간” 방식이고,
- 이 보간이 Self-Consistent (중간 시점을 거쳐도 동일 결과), 이라 완전히 결정론적이므로, 특정 해(Deterministic Minimizer)로 볼 수 있다.
- 논문에서는 이를 예시로 들어, “결정론적 보간도 Self-Consistent하다는 것”을 부록 C.1에서 증명하고 있습니다.
한 마디로, 식 (11) 하나가 “DDIM = 잡음 없이 와 섞어 시점 를 만듦”을 나타내고, 이 덕에 인덕티브 보간(=Self-Consistent)이 성립하며, 식 (7) 관점에서도 유일한 결정론적 해가 존재한다는 것이 이 부분의 핵심입니다.
Proposition 1
- <복습>
- <원문>
위 generalized interpolant가 이고, mild assumptions(“데이터나 네트워크가 충분히” 좋고, “보간식이 적절히 역함수를 갖는” 같은 조건)을 만족 하면,
- Eq. (7).의 loss를 0으로 만드는 deterministic 가 존재한다.
See Appendix B.6 for formal statement and proof. This allows us to define
for a neural network with parameter by default.
1. “잡음 없이” 보간한다는 건 무슨 뜻일까?
- 논문에서 보간(
generalized interpolant)은 원래 “평균값 + 잡음” 형태로 쓸 수 있습니다. - 그런데 여기서는 “잡음()이 없다”고 가정해요.
- 즉, 시점 에서 시점 로 데이터를 이동할 때, 추가로 섞이는 랜덤성이 전혀 없고,
- 가 오직 한 가지 식에 의해 딱 정해지는 겁니다 (결정론).
2. 결정론적 분포가 뭘 의미해?
라고 써서, 가 그 함수 결과에 100% 고정된다고 표현하죠.
Eliminating stochasticity
1. 기본 아이디어: “결정론적”으로 시점 샘플링
- 원래 확산 모델(Diffusion Model) 샘플링이나, 다른 유사 모델들은 시점 에서 시점 로 이동할 때 확률적 잡음을 여러 차례 섞어야 하는 경우가 많습니다. (generalized interpolant)
- 그러나 여기서는 DDIM의 결정론적 보간(interpolant)을 사용합니다.
-
DDIM Interpolant
- 식으로 표현하면, DDIM은 시점 에서 시점 로 바로 가는 (ODE 기반의) 식을 제공합니다.
- 일반적으로 DDIM 보간은 인 형태(추가 잡음이 없음)로, 입력 와 추정된 원본 를 조합해서 한 번에 를 구해요.
-
결정론적 모델
- 실제로 “”라는 신경망(혹은 함수)로, “시점 샘플 가 주어졌을 때, 원본 은 무엇인가?”를 추정합니다.
- 그 뒤, DDIM 식 안에 그 “”를 대입해 를 구하면, 전 과정이 결정론으로 구성됩니다.
3. 실제 샘플링 방식: 시점 에서의
논문 식에 따르면,
여기서
- 는 이미 “진짜 분포 ”에서 뽑은 시점 샘플.
- 예: 확산 모델에서 “이라면 완전 잡음 상태”, “이라면 원본 데이터”.
- 는 “와 시점 를 입력받아 원본 데이터()을 복원”하려는 신경망.
- 은 DDIM 공식을 통해 “”와 “”를 적절히 섞어, 최종 를 만들어내는 결정론적 식.
5. 결론: DDIM + Deterministic → 추가 랜덤 필요 없다
- 결론: “Eliminating Stochasticity”가 가능하다는 말은,
1) DDIM 보간 (추가 잡음 없음),
2) 결정론적 신경망 ,
3) 표준 가우시안()으로 잡음 범위만 설정,
→ 이 세 요소를 합치면, 확률적으로 샘플링해야 할 스텝 없이도 를 한 번에 만들 수 있다는 뜻. - 이것이 논문에서 의도하는 “Stochasticity 제거”의 요점입니다.
- 따라서, “ODE sampler” (DDIM 방식을 통한 단일 단계)로도 샘플링이 끝나며, 추가로 무작위화할 이유가 사라집니다.
Re-using for
<복습>
1. 왜 가 필요할까?
- 논문 식 (8)과 (6)을 보면 (또는 이와 유사한 구조를 보면),
- “시점 ”에서 샘플 가 진짜 분포 에서 나와야 한다는 조건이 등장합니다.
- “모델이 에서 로 가는 것과 에서 로 가는 것을 비교”하려면, 둘 다 진짜 분포 샘플이 있어야 평가(또는 학습) 가능하다는 식의 맥락을 상상할 수 있습니다.
2. 기존 방식: 새로 뽑아 만들기
- 원래라면, “시점 0에 있던 원본 ”와 “잡음 ”을 새로 뽑아, 시점 로까지 Forward (또는 역, 중간) 가는 과정을 통해 를 생성할 수 있습니다.
- 하지만 이렇게 하면 추가로 새 샘플을 계속 뽑아야 해서, 계산 부담도 커지고 샘플 변동 (“분산”)도 증가합니다.
3. 대안: “와 재사용해서 만들기”
- 논문에서는 “차라리 한 번 얻은 ” (이미 시점 에서 샘플링된 것)를 써먹자고 제안합니다.
- 그리고 DDIM을 이용해,
- 은 시점 로 가는 결정론 보간 식.
요점
- 이렇게 하면, “새로운 조합을 뽑지 않아도” 시점 샘플을 얻을 수 있음.
- 즉, “이미 시점 에 존재하던 ”에서 한 번에 로 결정론적으로 이동 가능.
4. 정당화: “가 이렇게 만들어져도 그대로 유지”
- 논문은 Appendix C.2를 인용하며,
“를 에서 DDIM 보간으로 만들었지만, 그 결과는 ‘원래의 시점 분포 ’와 동일하게 유지된다.”
- 이는 Self-Consistent나 Marginal-Preserving 같은 개념과 연관되어 있습니다.
- DDIM 보간이 중간 시점을 바꾸든 직접 가든 결과 분포가 동일하게 유지된다는 성질 덕분에,
- 시점 에서 만든 가 본래 분포와 충돌하지 않는 거죠.
5. 최종 결론
- “Re-using for ”:
1) 를 로 계산,
2) 이로써 새 샘플링 과정 없이 시점 샘플을 얻는다,
3) 그리고 시점 분포가 그대로 유지되므로 분산(오차)을 줄이고 효율적.
Simplified Objective
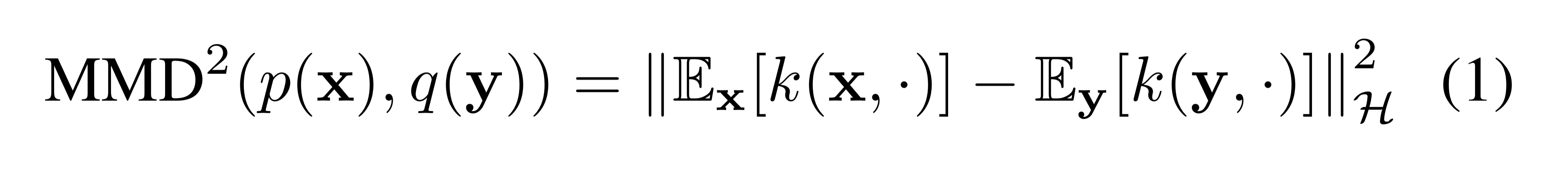
- 식 (1)은 아래의 식과 동치이고, 우리는 아래의 식을 objective로 씁니다.
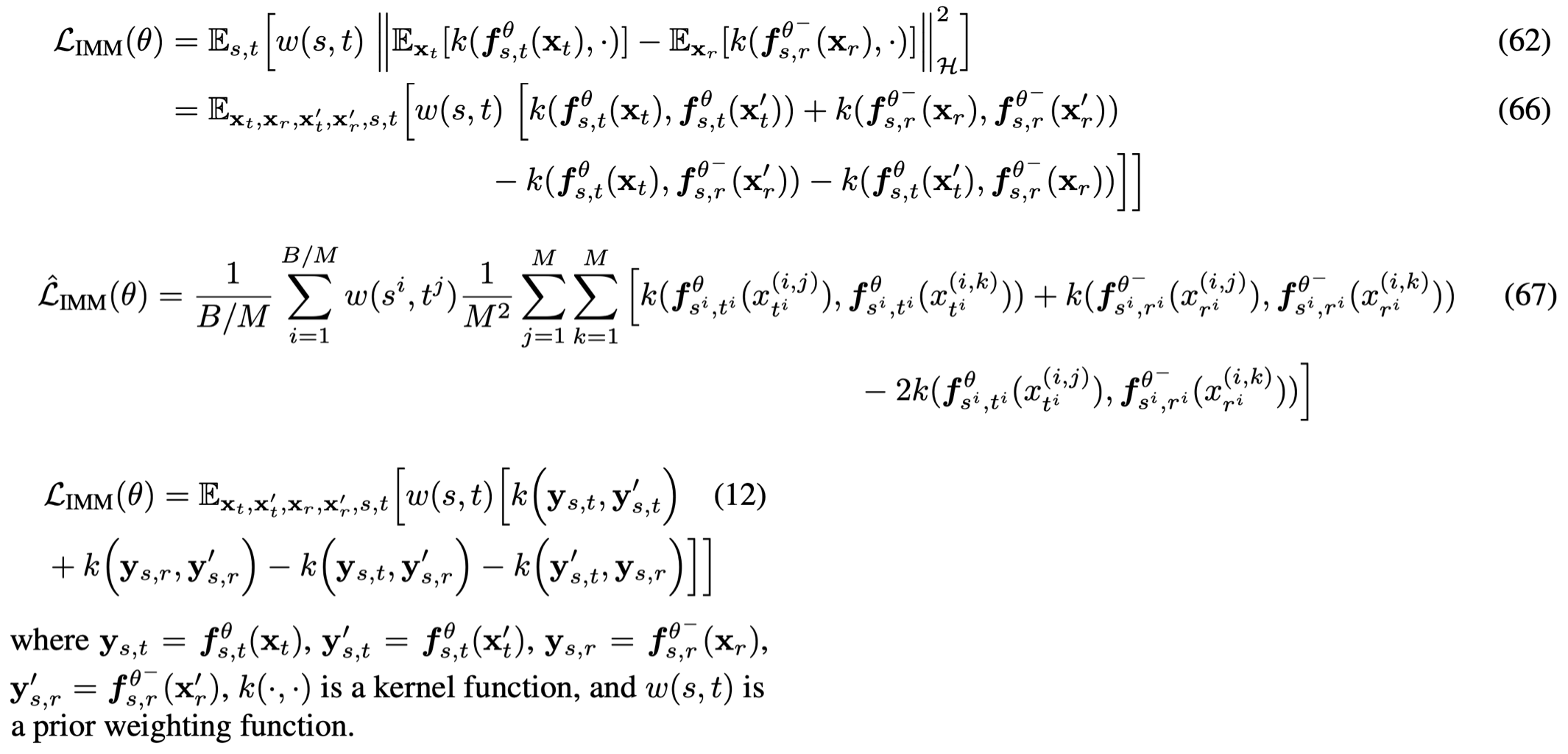
- 아래 그림 매우 중요. 확대해서 자세히 보자.
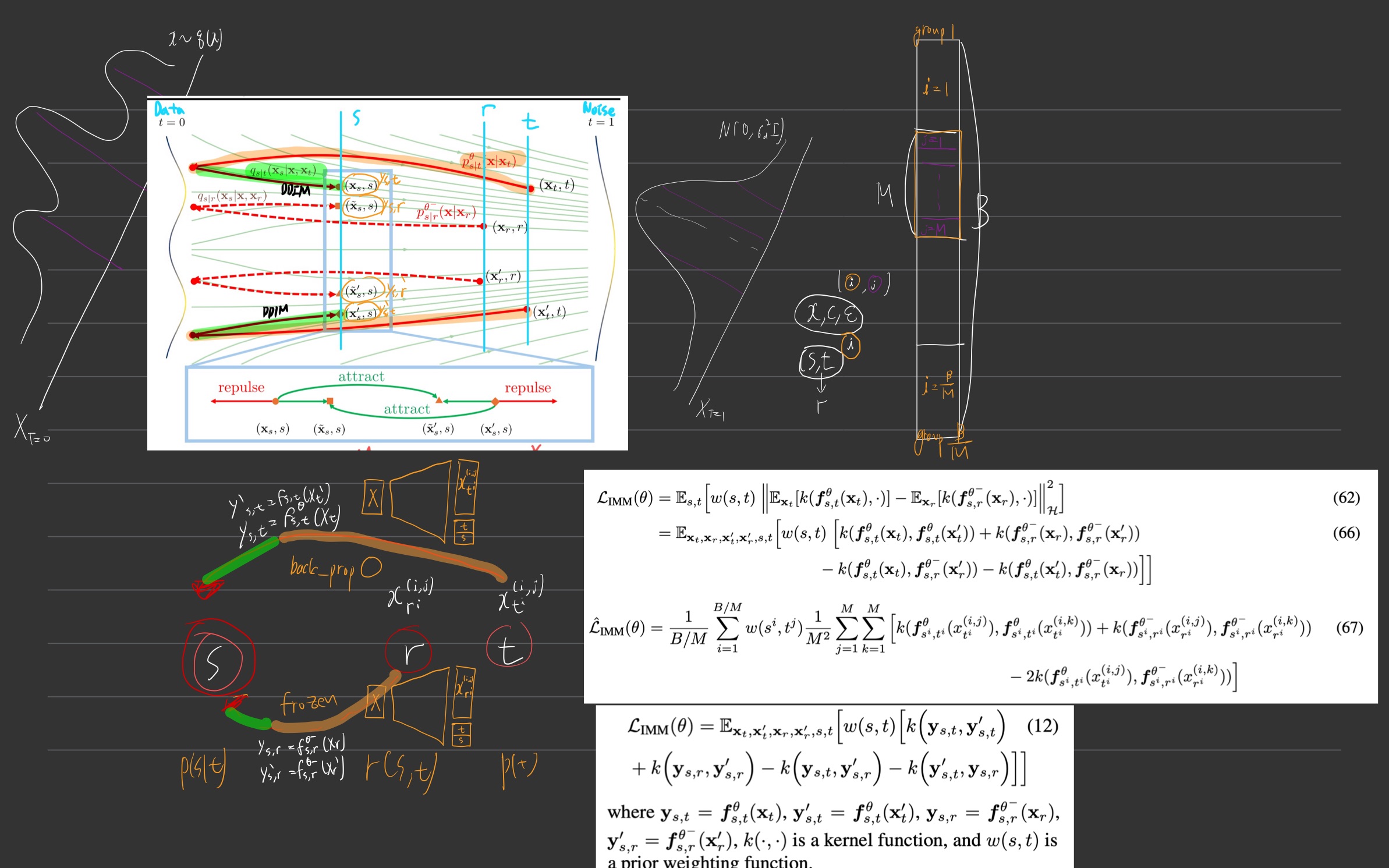
- “M을 늘린다고 해서, 모델 호출 수는 달라지지 않습니다"
- 구체적으로, 하나의 배치(B개의 예시)를 모델에 통과시킬 때, 이미 B개의 전파(forward pass)가 일어나므로,
- M을 조정해도 배치 내 구성만 달라지고 추가 모델 호출이 크게 늘지는 않는다는 의미예요.
- 즉, 배치 크기를 어떻게 분할해서 M개의 샘플씩 묶느냐의 문제지, 전체 forward pass 횟수는 여전히 “배치 B”번으로 동일하다는 이야기입니다.
Full training algorithm
- 아래 그림 매우 중요. 확대해서 자세히 보자.

classifier-free guidance
4.2. Other Implementation Choices
Flow trajectories
Network
Noise conditioning
Mapping function
Kernel function
Weighting and distribution
4.3. Sampling
- 아래 그림 매우 중요. 확대해서 자세히 보자.
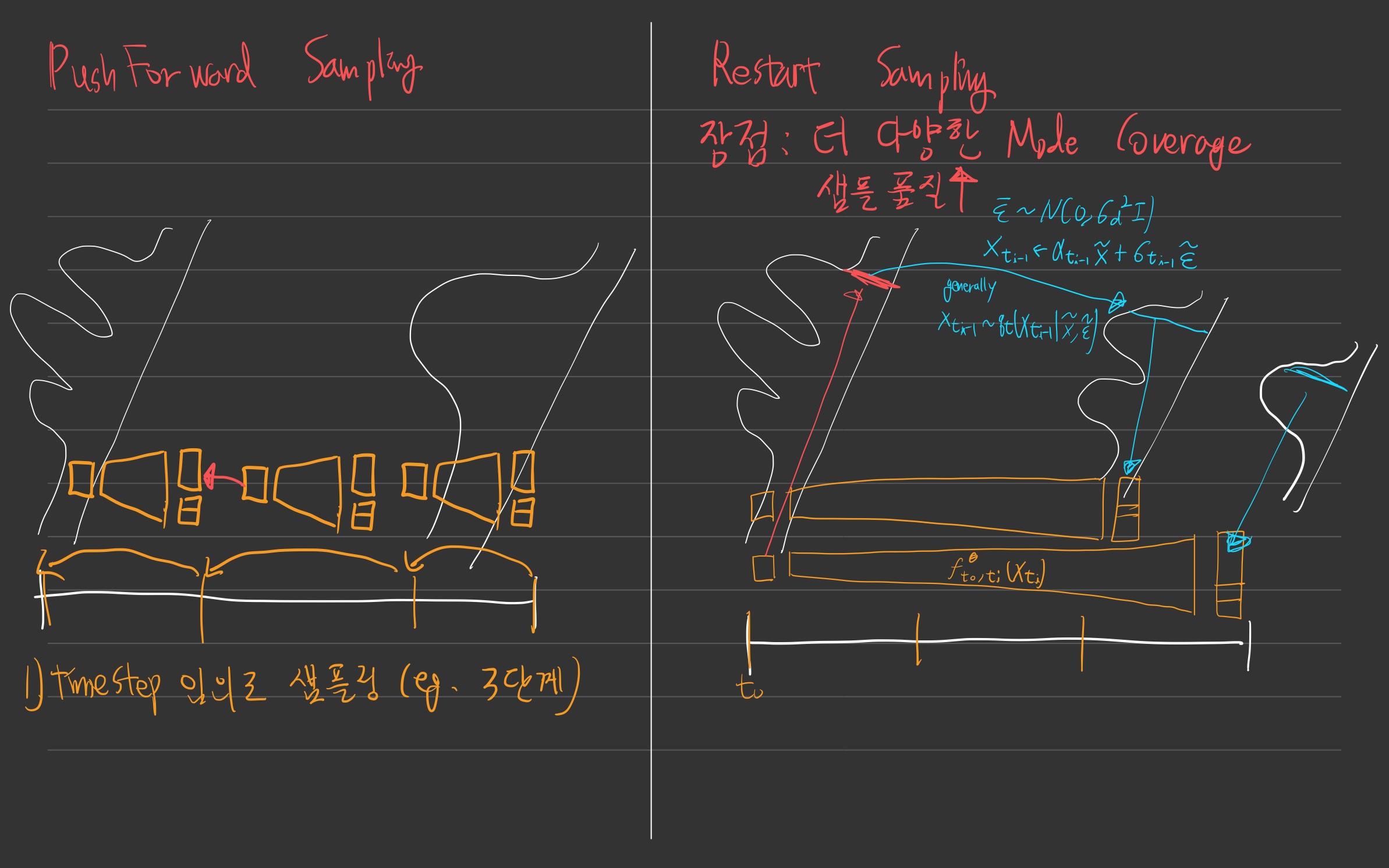
- restart sampling
- sampling 과정을 확률적으로 만든다.
- 더 다양한 mode coverage
- 샘플 품질 up


