Optimizing diffusion models for joint trajectory prediction and controllable generation

ad_official·2024년 12월 31일
0

realistic traffic agent modeling

목록 보기
1/6

바쁘신 분들을 위한 3줄 요약

  • Controllable multi-agent Traffic generation 을 위한 diffusion 방법론은 inference 속도에 문제가 있었는데, 이를 해결하기 위한 2가지 방법을 제시했다.
  • Optimal Gaussian Diffusion: "표준 가우시안이 아니라, 실제 데이터의 평균-분산을 활용해 최적화된 중간 t timestep에서의 가우시안에서 역확산을 시작” → 적은 단계(t -> 0)로도 실제 데이터에 가까운 샘플을 얻어 추론 속도 향상
  • Estimated Clean Manifold: “중간 noisy 데이터가 아닌, 현실적인 깨끗한 궤적 데이터에 직접 가이던스 그래디언트 적용” → 가이던스 그래디언트를 위해 매 스텝마다 역전파할 필요를 줄여 계산 효율 개선.

abstract

  • diffusion 모델의 장점: controllable generation
    • (추가적인 훈련 필요 없이) 추론 단계에서 그래디언트 기반의 guidance sampling을 통해,
    • 생성된 궤적 분포를 -> 추가 요구 사항(예: 충돌 방지 / 운전자 성향 등)에 맞게 변형할 수 있음!
  • 하지만 확산 모델은 inference 속도가 느리다 ㅠ
  • 해결책: Optimal Gaussian Diffusion (OGD) + Estimated Clean Manifold (ECM)
    • 위 두 방법론은, 생성 과정을 간소화하여 계산 비용을 줄임
    • 어떤 방법론인지는 아래에서 설명!

Introduction

diffusion의 계산 비용이 높은 이유 ?

1. 계산 비용이 높은 역 확산

  • 역 확산 과정은 본질적으로 하나의 확률미분방정식(SDE) 로 표현되는데,
    • 표준 가우시안 prior로 부터 역 확산을 시작하면 -> 그 공식(=SDE)을 엄격히 따르도록 모델이 짜여 있습니다.
  • dτ=−f(τ,t)dt+g(t)dwdτ = -f(τ, t)dt + g(t)dw
    • ττ: 시간 t에서의 궤적 (또는 상태)
    • f(τ,t)f(τ, t): (drift coefficient) 함수 (시간 t에서 궤적 τ의 평균적인 변화를 나타냄)
    • g(t)g(t): (diffusion coefficient) 함수 (시간 t에서 궤적 τ의 무작위적인 변화의 크기를 나타냄)
    • dwdw: 위너 과정(Wiener process) 또는 브라운 운동(Brownian motion) (무작위적인 움직임을 나타내는 확률 과정)
    • dtdt: 미소 시간
  • 기존에는 inference 속도를 높이기 위해, SDE의 정의(=각 단계에서 제거해야 할 노이즈 양 등)를 무리하게 생략하거나 “건너뛰는” 식으로 가속하는 연구가 많았음
    • 이렇게 하면 이론적으로 SDE에 어긋나는 근사나 편법이 필요하고, 그 결과 모델이 제대로 복원하지 못해 생성 품질(Quality)이 떨어질 위험이 높아짐

2. 계산 비용이 큰 가이던스 샘플링

  • 확산 모델에서 “가이던스”란,
    • “생성된 샘플이 특정 조건(예: 충돌 회피, 특정 트랙 유지 등)을 만족하도록 만드는 것”을 의미
  • Guidance cost function:
    • 생성된 궤적이, 우리가 원하는 특성에서 얼마나 벗어나는지를 비용(cost) 수식 형태로 계산
  • Guidance cost function는 Controllable multi-agent Traffic generation 문제에서 일반적으로 현실적인 궤적 데이터 매니폴드에서 정의함
    • 현실적인 궤적 데이터 매니폴드?
      • 실제로 가능한(물리적으로, 혹은 현실적으로) 데이터들이 형성하는 ‘공간’
      • 여기서 정의한 가이던스 비용만이 의미 있는 제약이나 목표가 됨(비현실적인 데이터에는 적용해봤자 쓸모가 없으니까)
  • 가이던스 샘플링은 아직 노이즈(잡음)가 남아 있는 중간 과정(시간 t)의 데이터(xtx_t)를 원하는 특성대로 수정하려고 합니다.
  • 연구자들 중에는 노이즈가 있는 상태에서 곧바로 가이드 비용 함수를 학습해보려는 시도가 있었지만[15],
    • 이렇게 하면 중간 단계에서 가이드 비용을 계산할 때 불안정한 수치 오류가 발생할 수 있다고 합니다[28,52].
  • guidance를 위해 추가 계산 비용이 드는 별도 학습 과정을 피하려고,
    • [16,28]에서는 확산 모델을 이용해 중간 노이즈 데이터를 먼저 깨끗한 상태로 투영(변환)한 다음,
    • 그 투영된 결과에서 가이드 비용을 계산하는 방법을 제안했어요 (아래 그림 참조).
    • 이 방법들은,
      • 우선 중간 잡음 데이터가 어떤 ‘깨끗한 상태’에 해당하는지를 추정(x^0\hat{x}_0)하는 것을 먼저 요구하고,
    • 그 다음 신경망 전체를 거꾸로 계산(역전파)해서 중간 노이즈 상태에서 어떤 식으로 수정해야 할지(그래디언트)를 구해줘야 합니다.
      • x^0\hat{x}_0에 대한 오차를 d(x^0)/d(x^t)d(\hat{x}_0)/d(\hat{x}_t) 로 backprop
    • 이렇게 중간 noisy 데이터 ↔ 깨끗한 데이터 사이를 매번 거치며 계산해야 하므로 연산 부담이 매우 커집니다.

related work

Diffusion models

  • inference 속도를 빠르게 하기 위해 아래의 2가지 track으로 학계에서 접근 중이라고 함
    • track 1: 역확산 과정(SDE)을 더 빠르게 해결하는 방법을 탐구
    • track 2: 더 빠른 추론을 달성하기 위해 역확산 과정을 초기화하는 것에 대한 대안 방법을 모색

Trajectory prediction

그림들

그림 1

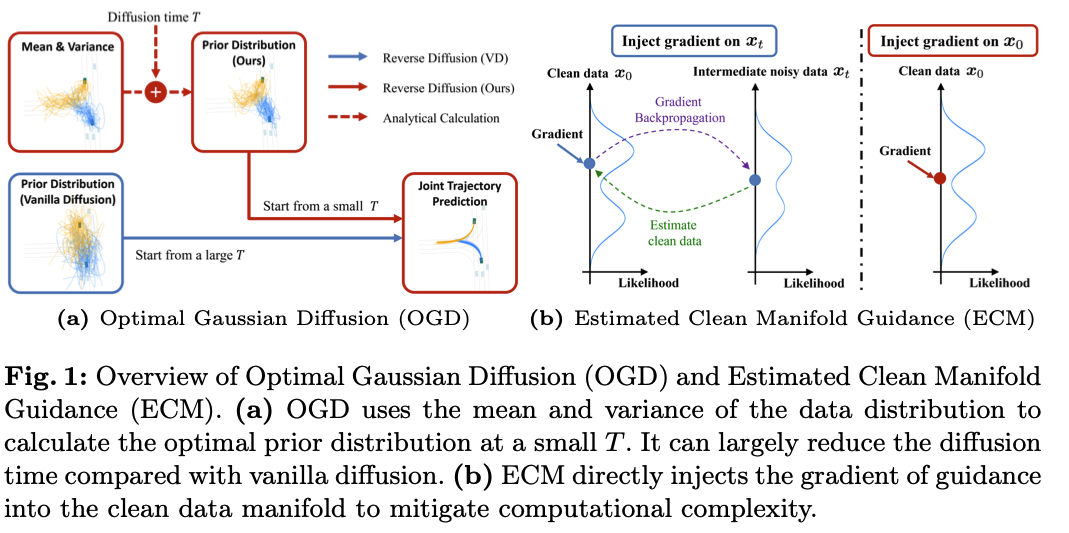
(a) Optimal Gaussian Diffusion (OGD)

  • 한줄요약: "표준 가우시안이 아니라, 실제 데이터의 평균-분산을 활용해 최적화된 중간 small T timestep에서의 가우시안에서 역확산을 시작” → 적은 단계(small T -> 0)로도 실제 데이터에 가까운 샘플을 얻어 추론 속도 향상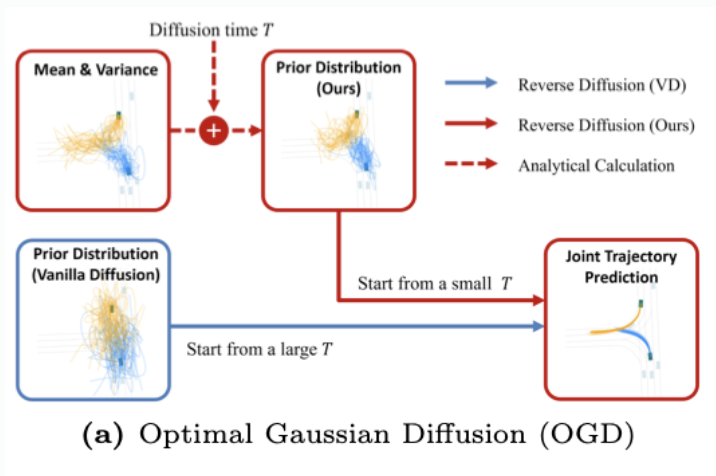
  • 구체적으로, forward 확산을 했을 때 어느 시간 tt(노이즈가 ‘중간 정도’인 순간)에 있는 데이터 분포 DtD_t를 기준으로, 이와 가장 비슷한 가우시안 분포를 찾습니다.
  • 그 다음, 그 가우시안 분포에서 샘플을 뽑아, 시간 t부터 0까지(즉, 중간부터 끝까지) ‘짧은 역확산’을 진행함으로써 최종 깨끗한 데이터를 얻게 되죠.
  • 따라서 처음부터 노이즈가 잔뜩 들어간 상태(표준 가우시안)에서 출발하지 않아도 돼서, 역확산 단계를 크게 줄일 수 있다는 장점이 있습니다.”
  • “연구진은 추가로 모델을 학습하지 않고도, 오직 데이터의 평균·분산(즉, 분포 통계 정보)만 있으면, 아래 2가지를 수학적으로 구할 수 있음을 보여주었습니다.
    • (1) 최적 가우시안 사전 분포(시작 분포)
    • (2) 시간이 지남에 따라 노이즈를 얼마나 더하거나 뺄지(perturbation)를 결정하는 최적 ‘perturbation kernel’
  • 여기서 말하는 perturbation이란, 순방향 확산일 때 데이터에 노이즈를 점점 섞는 과정, 역방향 확산일 때 노이즈를 점점 제거하는 과정을 통틀어 이르는 말이에요.
  • perturbation kernel은 그 노이즈 변화가 어떤 분포를 따르는지 나타내며,
  • ‘최적의 perturbation kernel’은 어떻게 노이즈를 주고받아야 최종적으로 좋은 품질의 샘플을 얻을 수 있는지 수학적으로 구한 해답이라고 보면 됩니다.
  • 또한, 사전 학습된 주변 궤적 예측 모델 [18, 24, 53]을 활용하여, 주변 궤적 분포의 평균 및 분산을 사용해 최적의 가우시안 prior을 계산하는 OGD의 실용적 구현을 도출

(b) Estimated Clean Manifold Guidance (ECM)

  • 한줄요약: “중간 noisy 데이터가 아닌, 현실적인 깨끗한 궤적 데이터에 직접 가이던스 그래디언트 적용” → 가이던스 그래디언트를 위해 매 스텝마다 역전파할 필요를 줄여 계산 효율 개선.
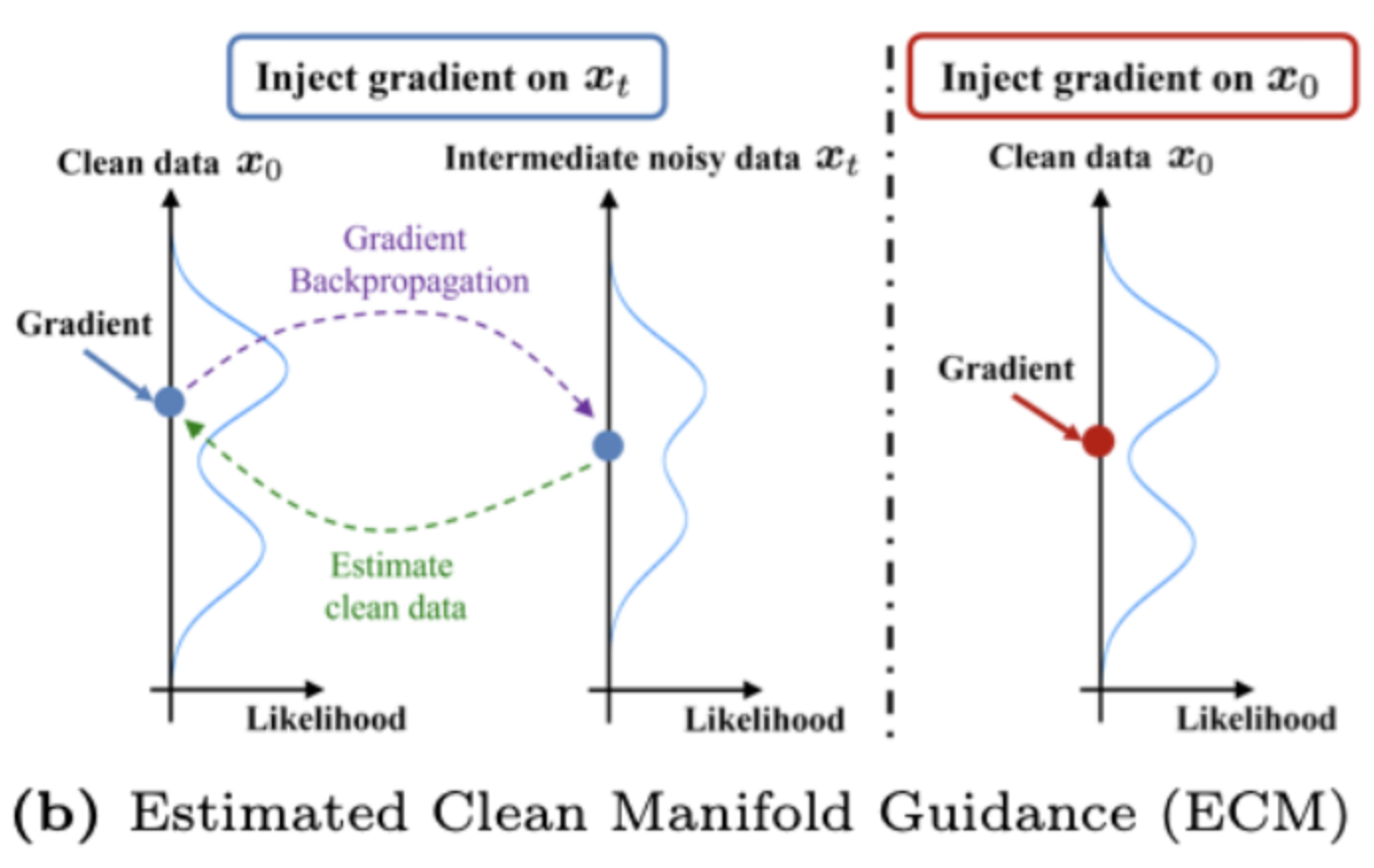
  • 왼쪽 그림: 기존 방법
  • 오른쪽 그림: 논문 제안 방법
  • Estimated Clean Manifold Guidance (ECM)은 가이던스 샘플링을 아래 2가지 목표를 동시에 만족하는 문제로 본다.
      1. 샘플이 “진짜 데이터”와 닮을수록 좋음 (가능성 최대화)
      1. 우리가 원하는 특성(예: 안전 주행, 특정 경로 준수 등)을 만족시키는 비용 최소화
  • 이미 추정된 깨끗한 데이터(x0^\hat{x_0})에 가이던스 그래디언트를 직접 적용 → 중간 노이즈 단계마다 복잡한 역전파를 거치지 않아도 됨.
    • 그 결과, 계산량이 크게 줄어든다.

Estimated Clean Manifold with Reference (ECMR)

  • 핵심 요약!
    • “ECMR은 주변 궤적 예측기로부터 얻은 ‘참조 공동 궤적’을 ECM의 초기값으로 삼아,
      • 여러 차량 간 상호작용으로 생기는 여러가지 가능한 미래 상황(a.k.a. 다중 모드)를 효율적으로 처리하고,
      • 노이즈 제거 및 가이던스 비용을 동시에 만족하는 궤적을 빠르고 정확하게 생성하는 방법”
    • 이렇게 보면, ECMR은 “다목적 최적화(현실성&제어가능성) + 현실적인 초기값 세팅 + 빠른 추론”을 모두 충족하려는 기법임을 알 수 있습니다.
  • 보충 설명
  1. ECMR(Estimated Clean Manifold with Reference)이란?
  • 기존 ECM(Estimated Clean Manifold) 기법에 “Reference trajectory” 개념을 더한 것입니다.
    • ‘Reference trajectory’이란, 이미 학습된 주변 궤적 예측 모델에서 뽑아낸 “대표적인 미래 궤적”을 뜻함.
  • 이렇게 얻은 Reference trajectory을 초기값으로 설정해 두면, ECM에서 수행하는 다목적 최적화가 더 빠르고 안정적으로 이루어집니다.
  1. 주변 궤적 예측기의 활용
  • 주변 궤적 예측 모델이 하는 일
    • 예: QCNet 등 이미 학습된 모델
    • 주변 차량(혹은 보행자 등)의 미래 궤적(몇 초 뒤 위치, 속도 등)을 예측해주는 역할을 함
    • 이 모델은 대량의 실제 주행 데이터를 학습했기 때문에, (“다중 모드”가 잘 나타나는 실제 도로 상황에서) 차량들이 보이는 대표적 패턴을 통계적으로 알고 있습니다.
  • 참조 공동 궤적 포인트(Reference trajectory) 추출
    • 이 예측 모델로부터, “가장 그럴듯한(혹은 가능성이 높은) 미래 궤적들”을 여러 개 뽑아낼 수 있습니다.
    • 그중에서 하나(또는 여러 개)를 대표 궤적(Reference)으로 삼아서, 내가 만들고자 하는 생성 샘플(궤적)의 초기값으로 사용합니다.
    • 이렇게 하면, 이미 현실성이 높은 시나리오에서 출발하기 때문에, 이후의 최적화 과정이 훨씬 간단해집니다.
  1. ECMR(Estimated Clean Manifold with Reference)의 작동 원리
  • ECM(Estimated Clean Manifold) 복습
    • ECM은 깨끗한 데이터 매니폴드(노이즈 제거 후 실제로 가능한 궤적들이 모여 있는 공간) 위에서,
    • (a) 데이터 분포에 잘 맞는지와 (b) 가이던스 비용(원하는 특성 충족도) 두 가지 목표를 동시에 만족하도록 다목적 최적화를 합니다.
    • 이 과정을 통해, “노이즈 제거 + 원하는 특성 반영”을 빠르고 효율적으로 달성하는 기법
  • ECMR: ECM + Reference
    • 여기에 주변 궤적 예측 모델로부터 얻은 참조 궤적을 더해주면,
    • 최적화(생성) 시작점을 이미 현실적이고 적절한 지점으로 설정할 수 있습니다.
    • 그 결과, 모델이 다중 모드를 더 잘 처리하고, 수렴도 빠르게 일어납니다.
    • 즉, “다양한 시나리오를 모두 고려하면서도 계산량을 줄이고, 보다 ‘그럴듯한’ 궤적을 생성하기 쉬워지는” 이점이 생기는 것이죠.
  1. ECM의 장점 (ECMR도 같은 장점을 공유)
  • 빠른 추론 시간
    • 기존 “가이던스 그래디언트” 방식은 각 diffusion 단계마다 네트워크 전체 역전파를 수행해야 했지만,
    • ECM/ECMR은 “깨끗한 매니폴드 위에서 직접 최적화”하기 때문에, 중간 잡음 상태마다 복잡한 연산을 안 해도 됨.
    • 따라서 전체 추론 시간이 크게 감소합니다.
  • 좋은 성능
    • 깨끗한 매니폴드 위에서 “실제 데이터 분포 적합도 + 가이던스 비용 최소화”를 직접 조정할 수 있어, 생성 결과의 품질이 높아집니다.
    • 특히 ECMR은 Reference trajectory을 초기화에 사용하므로, 다중 모드가 존재하는 복잡한 도로 상황에서도 안정적으로 좋은 결과를 얻을 수 있습니다.

그림 2: 좋은 성능을 내는 이유 분석

  • 그림의 가로축
    • 최적화하려는 변수(또는 trajectory 샘플의 상태)
  • 그림의 세로축
    • log⁡qθ(s0)\log q_\theta(s_0): 샘플 s0s_0가 데이터 분포(혹은 ‘likelihood 분포’)에서 얼마나 실제 세상에 있을법한지”를 나타내는 로그 확률 개념
    • −J(s0)-\mathcal{J}(s_0)는 “가이던스 비용" 관련된 값

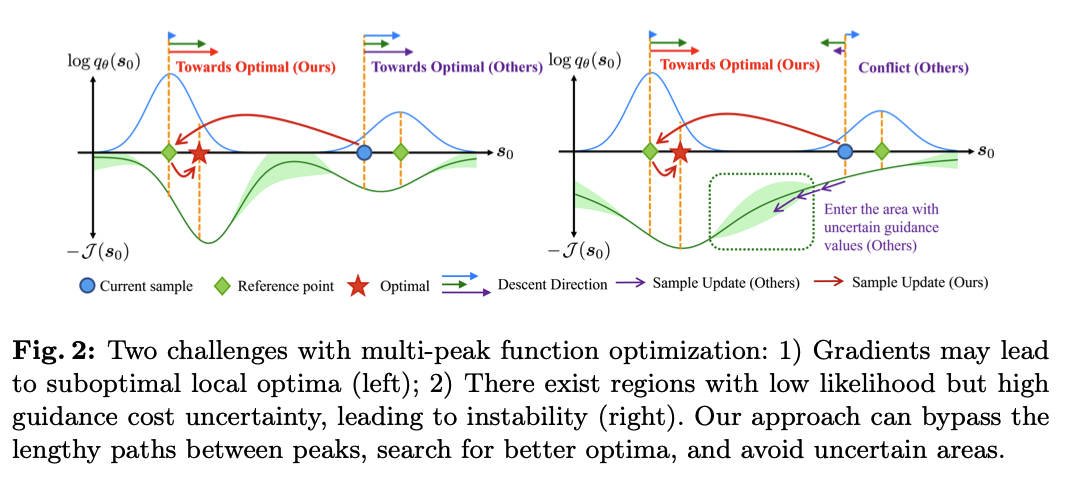
전체적 설명: Reference Joint Trajectories

  • 정리
      1. 다중 모달 문제: 여러 봉우리가 있는 확률 분포에서는, 샘플링 과정이 특정 봉우리에 갇혀버리거나, 봉우리 사이 이동 시 불안정해질 수 있음.
      1. Reference Joint Trajectories: 기 학습된 궤적 예측 네트워크를 이용해서, 미리 높은 확률의 궤적들을 조합·평가해 “비용이 낮은” 궤적을 초기값으로 선택 → 지역 최적해 함정을 피하고, 수치적 불안정도 줄임. ( 위 그림의 초록색 다이아몬드들)
      1. ECMR: ECM 기법 + 참조 궤적. 가이던스 비용과 가능성(확률)을 동시에 고려하면서, 초기값을 잘 잡아 다중 모드 상황에서 더 효율적으로 최적 해를 찾는 방법.
  • 문제 상황
    • 원하는 특성(가이던스 비용)이 낮은 궤적을 만들려면, 가능성이 높은 구역(높은 확률 밀도 영역) 안에서 비용이 낮은 궤적을 찾아야 합니다.
    • 하지만 실제 도로 환경에서는 궤적 분포가 다중 모달(multimodal) 형태를 띱니다. (다중 모드 특성)
    • 따라서 최적해가 여러 개 생길 수 있고, 각각 서로 멀리 떨어져 있을 수 있습니다.
  • 문제점
    • 가이던스 샘플링 기법들([15,16,28,52] 그리고 본문의 ECM 포함)은 대체로 다음 두 가지 문제에 부딪힙니다 (그림 2 참고):
    • 역확산 과정을 거칠 때, 현재 위치 주변(예: 초기값 주변)에서 복원 + guidance 를 수행하면, local optimum에 빠질 위험이 있음. (왼쪽 그림)
    • 한 봉우리(peak)에서 gradient descent로 다른 봉우리로 옮겨가려면, 낮은 가능도(=분포가 희박한 구역, 깨끗한 매니폴드가 아닌 구역)를 반드시 통과해야 하는데, 이때 수치적 불안정성이 생겨 샘플링이 쉽지 않음. (오른쪽 그림)
      • 개인적 생각: 아마 likelihood가 낮은 쪽으로 역확산 복원 과정이 이루어지기 어렵다는 뜻 같음
  • 해결책: Reference Joint Trajectories
  • 핵심 아이디어
    • “가능성이 높은(high-likelihood) 참조 궤적(reference trajectory, 그림의 초록색 마름모들)을 (기 학습된 궤적 예측 네트워크를 활용하여) 미리 만들어 두고, 그중 비용이 가장 낮은 궤적을 초기값으로 활용하자.”
    • 이렇게 하면, 다중 모드 사이를 억지로 뛰어다니지 않고도, 가장 알맞은 봉우리(peak) 근처에서 시작하므로 최적해에 도달하기 쉬워집니다.
  • 구체적인 방법
      1. 기 학습된 궤적 예측 모델들은 각 차량(또는 각 주체)의 궤적에 대해 가능성이 높은 샘플들을 만들어낼 수 있습니다
      • 예: R={Ri}i=1nR = \{R_i\}_{i=1}^n은 각 주체(차량 등)별로 얻은 마진 샘플 집합.
      1. 이 샘플들을 조합해 “가능성이 높은 공동 궤적(joint trajectory) 후보”들을 여러 개 만들어냅니다.
      1. 각 조합에 대해 가이던스 비용 J(w)J(w)(예: 충돌 여부, 특정 제약 만족도 등)을 계산하고, 그중 가장 비용이 낮은 궤적을 참조(reference)로 선정
      • 즉 likelihood도 높고, guidance도 높은 지점에서 복원 과정을 시작하자!
      1. 이 참조 궤적을 ECM(가이던스 샘플링 기법)의 초기값으로 사용하면,
      • 지역 최적해에 덜 빠지고,
      • 다중 모드를 가볍게 피해 가면서,
      • 안정적으로 최적의 궤적을 찾을 수 있습니다.
  • 알고리즘 ECMR
    • 본문에서는 이 과정을 ECM with reference joint trajectories(ECMR)라고 부르며,
    • 핵심은, 기존 ECM과정(가이드 비용 최소화 + 분포 적합도 최대화)에, 미리 뽑아 둔 참조 궤적을 활용해 초기 상태를 설정하고, 이후 가이던스 샘플링을 수행한다는 점입니다.

실험적 검증

  • 제안된 Optimal Gaussian Diffusion (OGD) + Estimated Clean Manifold (ECM) 방법론을 실제 작업에 평가하기 위해,
    • 우리는 사전 학습된 주변 예측 모델 QCNet [53]을 활용한 Optimal Gaussian Diffusion 모델을 구현하고, Argoverse 2 데이터셋에서 검증
  • 실험 결과, OGD는 (표준 확산 모델의 1/12에 해당하는 확산 단계 만으로도) 기존에 비해 더 나은 공동 궤적 예측 성능을 달성
  • 또한, OGD와 결합된 Estimated Clean Manifold with Reference은
    • 기존의 가이던스 샘플링 접근법 [16, 28]을 사용하는 표준 확산 모델과 동일한 수준의 현실성 점수를 유지하면서도,
    • 가이던스 비용이 현저히 낮은(약 1/5의 추론 단계) 샘플을 생성할 수 있음을 보여줍니다.
profile
ad_official
ad_official
다음 포스트

[generation][22, 3][203] Stochastic Trajectory Prediction via Motion Indeterminacy Diffusion

0개의 댓글