• https://openaccess.thecvf.com/content/CVPR2022/papers/Gu_Stochastic_Trajectory_Prediction_via_Motion_Indeterminacy_Diffusion_CVPR_2022_paper.pdf
• https://openaccess.thecvf.com/content/CVPR2022/supplemental/Gu_Stochastic_Trajectory_Prediction_CVPR_2022_supplemental.pdf
  • 2022, 196회 인용
• https://github.com/gutianpei/MID
  • 192 stars

핵심 3줄 요약

• diffusion 을 prediction에 적용하면, trajectory의 여러 가능성(다중 모드)을 모두 확률적으로 학습 가능하며, 학습 중에 없었던 데이터에 대해서도 inference시 높은 성능 기대 가능 (DDPM 적용함)
• GAN은 diffusion보다 현실에 있을법한 궤적을 잘 생성하지만, 다중 모드를 학습하기 어렵고 적대적 학습으로 인해 불안정. Conditional VAE은 현실적이지 않은 궤적을 생성한다는 단점
• 본 논문은 Unet 구조 대신 transformer 구조를 사용하였음. 그리고 inference 시, 한번에 1 agent의 궤적만 예측

Abstract / Introduction

• 
• 기존의 보행자 경로 예측 방법들(GAN, CVAE)은 보통 '잠재 변수'라는 것을 사용해서 여러 가능성(다중 모드)을 표현했지만,
  • GAN
    • 모든 가능한 미래 경로에 걸쳐 분포를 확산시키는 방식 (모든 가능한 미래 경로에 대한 가능성을 넓게 펼쳐서 보여줌)
    • 단점: 적대적 학습으로 인해 훈련 과정이 불안정할 수 있음
  • Conditional VAE:
    • 미래 경로의 다중 모드 분포를 인코딩 (미래 경로의 여러 가능성들을 압축하여 표현)
    • 단점: 부자연스러운 경로 생성
• MID (Motion Indeterminacy Diffusion): 운동 불확정성 확산, 보행자 경로 예측을 위해 diffusion을 적용
  • 경로 특징에 노이즈 잠재 변수를 추가하여 불확실성을 얻는 다른 확률적 예측 방법과 달리, 우리는 운동 불확실성 변화 과정을 명시적으로 시뮬레이션
  • 불확실성을 명시적으로 모델링
• diffusion 접근법의 장점
  • 다양하고 사실적인 trajectory 생성 (mode coverage)
  • OOD robustness
    • 학습 중에 없었던 데이터에 대해서도, inference시에 높은 성능 도출 가능성
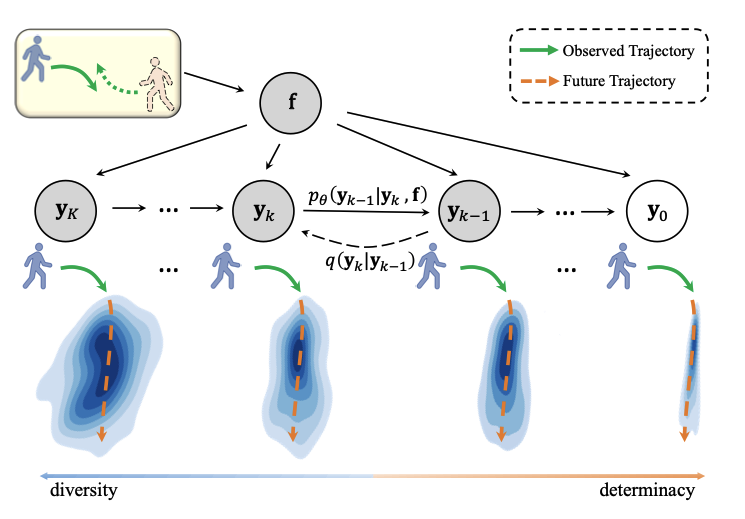
• 정방향 확산: 이 과정에서는 실제 보행자의 경로(y_0) 에 점진적으로 노이즈를 추가하여, 불확실성이 최대화된 상태(y_K), 즉 "어디로든 갈 수 있는 모호한 영역" 을 만듭니다.
• 역방향 확산: 이 과정에서는 "어디로든 갈 수 있는 모호한 영역(y_K)" 에서 시작하여, 점진적으로 불확실성을 제거하면서, 결국에는 하나의 구체적인 경로(y_0) 를 생성합니다.
• 조건부 역 확산 -> 과거 정보 활용:
  • MID는 과거 경로 정보(f)를 활용하여, 더 정확한 예측을 할 수 있습니다.
  • f는여러 사람들의 과거 경로에서 추출된 정보로, 보행자의 움직임 패턴, 주변 환경과의 상호작용 등을 -> 'state embedding'으로 압축
• 점진적 불확실성 제거 (역확산 과정):
  • $p_θ(y_{k-1} | y_k, f)$
    • y_k: 현재 단계 k에서의 불확실한 상태 (예: 노이즈가 섞인 궤적)
    • y_{k-1}: 이전 단계 k-1에서의, 불확실성이 줄어든 상태 (예: 노이즈가 덜 섞인 궤적)
    • f: 과거 경로 정보
    • p_θ: 이 과정을 제어하는 규칙 (신경망)
• 그리고 '트랜스포머'기술을 사용한 '확산 모델'을 만들어서 경로가 시간에 따라 어떻게 변하는지를 학습시킵니다.
• Stanford Drone 데이터셋과 ETH/UCY 데이터셋과 같은, 보행자 경로 예측에 널리 사용되는 데이터들을 가지고 실험해 본 결과, 저희가 제안한 방법이 매우 우수한 성능을 보인다는 것을 확인했습니다.
• 다양성 조절:
  • 역방향 확산의 단계 수(K)를 조절하여, 예측의 다양성과 확실성 사이의 균형을 맞출 수 있습니다.
  • K가 크면: 더 많은 단계를 거쳐 노이즈를 제거하기 때문에, 더 사실적이고 결정론적인 경로를 생성합니다.
  • K가 작으면: 더 적은 단계를 거쳐 노이즈를 제거하기 때문에, 더 다양하지만 덜 사실적인 경로를 생성합니다.

---

---

3. 제안 접근법

• 

3.3. Training Objective

• DDPM(https://velog.io/@jk01019/Diffusion-오렌지-노트-한국어-정리) 을 그대로 가져와서 적용한 논문
• 손실 함수는 아래와 같음
• $L(θ, ψ) = E_{ε, y_0, k} || ε - ε_{(θ, ψ)}(y_k, k, x) ||²$ (식 10)
  • 여기서 $ε$ ~ $N(0, I)$, $y_k = √(ᾱ_k) y_0 + √(1 - ᾱ_k) ε$이고, 학습은 각 단계 $k ∈ 1, 2, ..., K$에서 수행됩니다.

3.4. Inference

• 역 확산 과정이 학습되면, 우리는 노이즈 가우시안 분포 $y_K$ ~ $N(0, I)$에서 역 확산 과정 $p_θ$를 통해 그럴듯한 경로를 생성할 수 있습니다.
• (9)의 재매개변수화를 사용하여 $y_K$에서 $y_0$까지의 경로를 다음 식 (11) 같이 생성합니다.
  • 식 (9): $μ_θ(y_k, k, f) = (1 / √(α_k)) (y_k - (β_k / √(1 - ᾱ_k)) ε_θ(y_k, k, f))$
    • DDPM 논문에 나온 그대로임
• $y_{k-1} = (1 / √(α_k)) (y_k - (β_k / √(1 - ᾱ_k)) ε_θ(y_k, k, f)) + √β_k z$ (식 11)
• 여기서
  • $z$는 표준 정규 분포의 확률 변수이고,
  • $ε_θ$는 이전 단계의 예측 $y_k$, 상태 임베딩 $f$, 그리고 단계 $k$를 입력으로 받는 학습된 신경망

3.5. Network 구조

• 
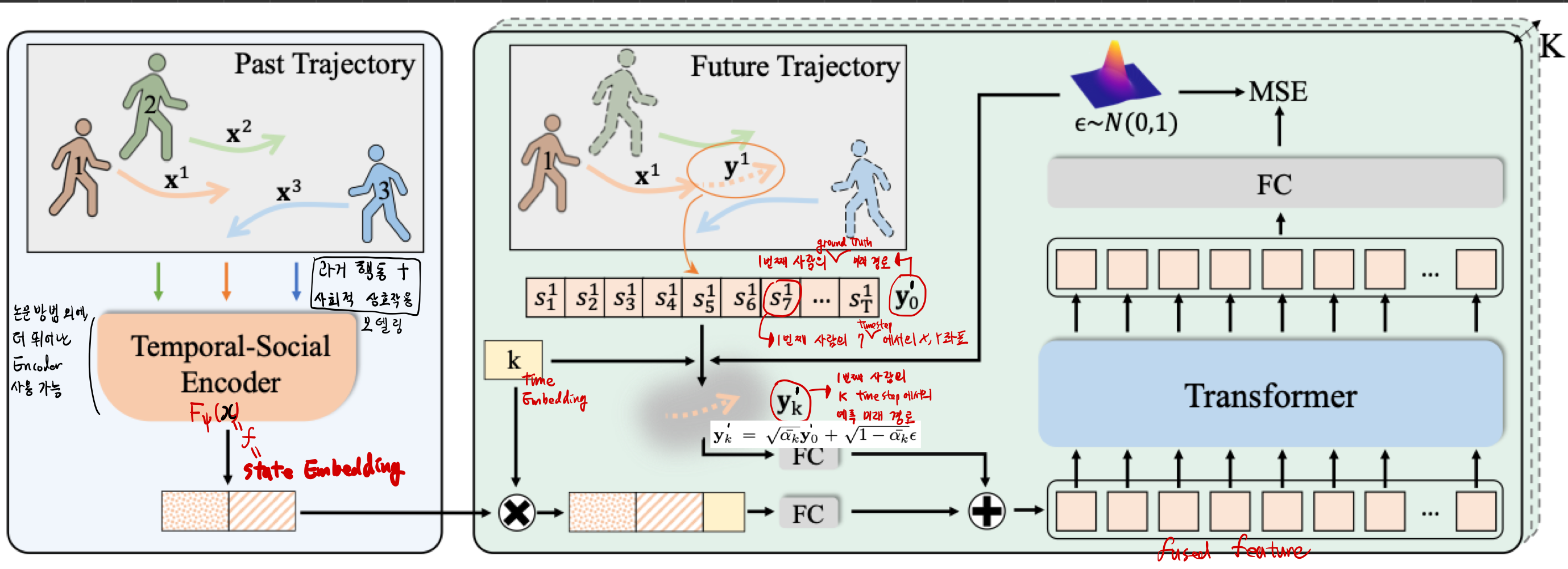
• 이미지 기반 확산 모델에서 널리 사용되는 UNet [36]과 달리, 우리는 MID를 위한 새로운 트랜스포머 기반 네트워크 구조를 설계했습니다.
• 트랜스포머를 사용하면 모델이 경로 예측 작업을 위해 경로의 시간적 의존성을 더 잘 탐색할 수 있습니다.
  • 구체적으로, MID는 두 가지 주요 네트워크로 구성됩니다:
    • 관찰된 과거 경로와 사회적 상호작용을 통해 state embedding을 학습하는 매개변수 ψ를 가진 인코더 네트워크
    • 역 확산 과정을 위한 θ로 매개변수화된 트랜스포머 기반 디코더
• k 단계에서, 먼저 경로에 노이즈를 추가하여 y_k = √ᾱ_k y_0 + √(1 - ᾱ_k) ε를 얻습니다. (즉, 실제 경로 y_0에 노이즈 ε를 섞어서 불확실한 경로 y_k를 생성합니다.)
• 동시에, time embedding을 계산하고, 이를 관측된 경로의 특징과 연결(concatenate) 합니다.
• 그런 다음, fully-connected layer을 적용하여 경로 $y_k$와 조건 $f$를 모두 업샘플(upsample) 하고, 그 출력들을 합산하여 융합 특징(fused feature) 을 만듭니다.
• 또한 다른 경로 타임스탬프 t에서의 위치 관계를 강조하기 위해 합산에 사인 함수(sinusoidal function) 형태의 위치 임베딩(positional embedding)을 도입
• 마지막으로, positional embedding이 포함된 융합 특징은 복잡한 공간-시간적 단서를 학습하기 위해 트랜스포머 네트워크에 입력됩니다.
• 트랜스포머 기반 디코더 네트워크는 경로의 시간적 의존성을 충분히 모델링하기 위해 3개의 셀프 어텐션 레이어(self-attention layer)로 구성되며, 고차원 시퀀스를 입력으로 받아 동일한 차원의 시퀀스를 출력합니다.
• fully-connected layer을 사용하여 출력 시퀀스를 경로 차원으로 다운샘플(downsample)합니다.
• 우리는 마침내 현재 반복(iteration)에 대한 네트워크를 최적화하기 위해, 출력과 무작위 가우시안 사이에 평균 제곱 오차(MSE) 손실을 위 (10) 식과 같이 수행합니다.

Limitation

• inference time이 말도 안되게 오래 걸림