Gradient Vanishing
-
다층 퍼셉트론 오차역전파 적용시, 입력층으로 갈수록 기울기가 작아지는 현상
-
gadient vanishing 이유
- activation function으로 적용한 sigmoid함수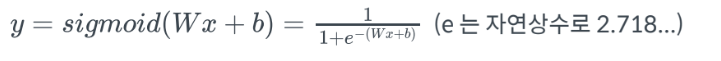
- 결과 값을 0과 1 사이의 값으로 조정하여 반환 => 0~100%의 확률값을 가질 수 있음
-
sigmoid 미분
- 시그모이드 미분은 무조건 1보다 작음- x<1이면, x^10, x^100과 같이 x를 곱할수록 최종값은 0에 수렴
-
다층 퍼셉트론 구조와 sigmoid
- 오차 역전파 계산시, activation function도 미분
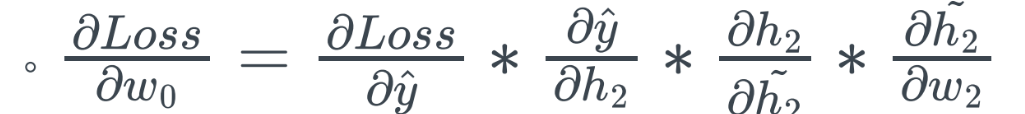
- activation function 미분 값이 1보다 작을 경우, 레이어가 입력에 가까울수록 해당 값이 0에 가까워질 수 있음(gradient vanishing 현상) -
gradient vanishing 이슈 해결 방안
- ReLU함수
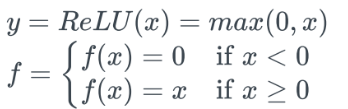
- 미분값은 x>=0일떄 1, x<0일떄 0이므로, gradient vanishing 이슈를 어느정도 보완 - x>=0이면 미분이 1이므로, 학습속도가 sigmoid보다 빠른편 (sigmoid 함수는 x값이 커지면 y가 1에 가까워지므로, 기울기가 낮아져 학습속도가 현저히 낮아짐)
Optimizer
- 주요 optimizer
- 딥러닝의 학습 : 손실값이 가장 작은 모델을 만드는 것
- 학습은 손실함수의 최소값을 찾아가는 과정=> Optimization(최적화)
=> 수행하는 알고리즘 : optimizer
- 대표적인 optimizer가 gradient descent를 기반으로 한 SGD, 이외에 더 다양한 optimizer가 제안됨- Adam optimizer가 주로 사용됨
- Momentum
- SGD에 관성(momentum)이 추가된 optimizer- 관성 적용을 위해 v가 추가됨
- SGD :
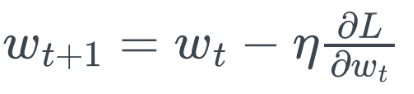
- Wt+1 =Wt - lr*(θL/θwt) = 가중치t - 학습률*t시점gradient- L : 손실함수
- Momentum
- Wt+1= Wt-Vt
- Vt=Γ*Vt-1 + lr*(θL/θwt) = 감마비율*(t-1시점 gradient) + 학습률*(t시점gradient)
- Γ : [0,1] 사이 값
- g1=t시점 gradient이라하면,- v1=g1 / v2=g2+Γ*g1/ v3=g3+Γ*g2+Γ^2*g1...
- Γ 곱할수록 값 작아져 오래 전 단계의 gradient 영향 적게 받게 됨
- 같은 방향으로 이동하게 되면 가속도가 붙게 되어 local minima를 탈출할 수도 있음
- v1=g1 / v2=g2+Γ*g1/ v3=g3+Γ*g2+Γ^2*g1...
- Vt=Γ*Vt-1 + lr*(θL/θwt) = 감마비율*(t-1시점 gradient) + 학습률*(t시점gradient)
- Wt+1= Wt-Vt
- Nesterov Accelerated Gradient(NAG)
- NAG는 mementum 계산 시, momentum에 의해 발생하는 변화를 미리 보고 momentum을 결정-
주요 수식
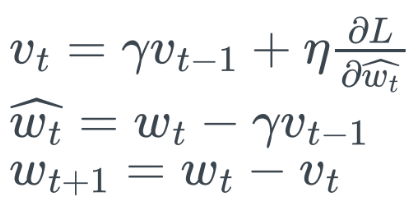
- NAG 방식은 wt 위치에서 wt+1의 gradient를 계산하고자함 -
앞 단계의 gradient를 근사해 현재의 momentum을 조정
수식 이해
-
- Adaptive Gradient(AdaGrad)
- (SGD, Momentum, NAG 모두 파라미터 업데이트에 동일한 lr값 적용)- AdaGrad : 학습률 감소 기법으로 개선하고자 함
- 경사하강법의 t번째 gradient는 현재 시간에 얼마나 변화되었는지 지표
- 각 Wi에 대한 gt의 제곱을 누적한 값을 통해, 지금까지 변화정도를 계싼하고 이를 lr에 적용
- iteration 중, 많이 움직이는 경우(기울기가 컸던), 해당 iteration의 lr는 그만큼 작아지므로, 학습률이 각 iteration마다 다르게 적용됨 (iteration별 맞춤형 lr의 적용이 가능)
- 경사하강법의 t번째 gradient는 현재 시간에 얼마나 변화되었는지 지표
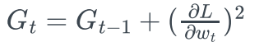
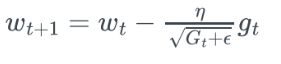
- Adagrad는 t가 증가함에 따라 Gt가 점점 커져 lr가 점점 소실되는 문제가 있음
- AdaGrad : 학습률 감소 기법으로 개선하고자 함
- RMSProp
- Adagrad에서 발생한 t가 증가함에 따라 lr가 점점 소실되는 문제 해결
- G를 구할떄, 합을 이용하지 않고 지수가중평균을 이용- gt : t번째 gradient
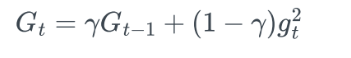
- Γ와 (1-Γ)를 통해 지수가중평균 방식으로 업데이트
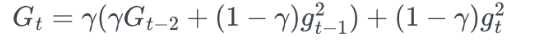
- Γ가 계속 곱해지면, 값이 갈수록 작아져, 오래된 데이터일 수록 더 적은 영향을 미치도록 함- 데이터가 오래될수록 지수적 감쇠
-
- 데이터가 오래될수록 지수적 감쇠
- Γ와 (1-Γ)를 통해 지수가중평균 방식으로 업데이트
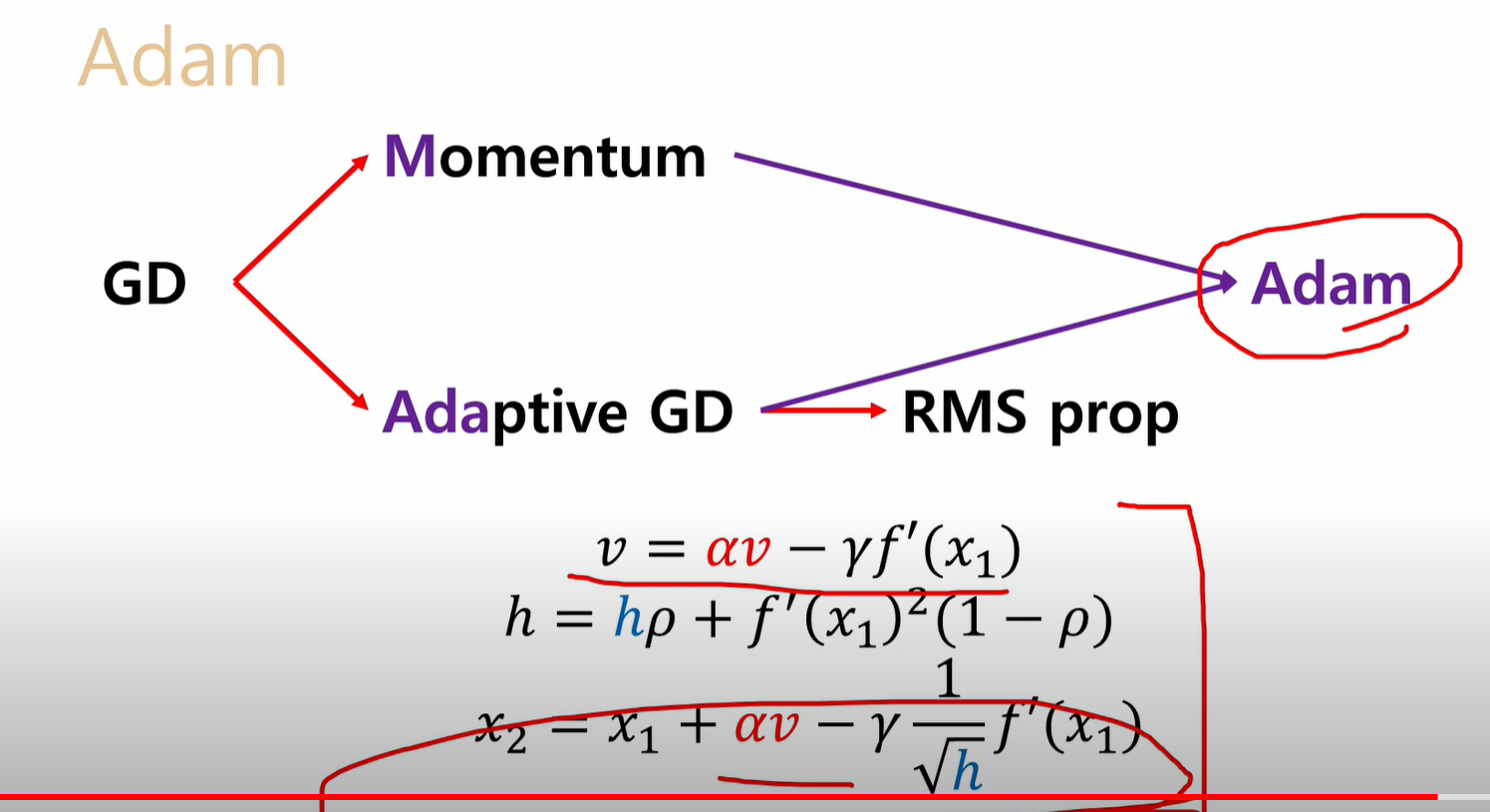
- Adam(Adative Moment Estimation)
- 가장 많이 사용하는 Optimizer- Momentum과 RMSProp을 결합한 느낌
- Momentum : 이전의 gradient 경향을 적용
- RMSProp : Lr가 점점 소실되는 문제를 해결해, 이전의 lr 경향을 적용함
- Momentum : 이전의 gradient 경향을 적용
- 수식
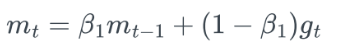
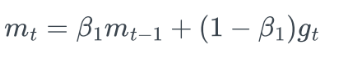
-
gt= t번째 gradient
- 지수 가중 평균을 이용한 Momentumqkdtlr
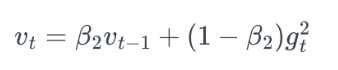
- 오래된 데이터의 값을 작게해 lr의 감쇠를 막는 RMSProp 방식- Momentum + RMSProp 최종 식
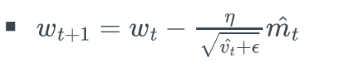
-
- Momentum과 RMSProp을 결합한 느낌