Chapter
-Algorithm with python-
1. 검색 알고리즘
(1) 선형 검색
(2) 이진 검색
2. 순위 알고리즘
3. 정렬 알고리즘
4. 최댓값 알고리즘
5. 최솟값 알고리즘
6. 최빈값 알고리즘
1. 검색 알고리즘
(1) 선형 검색(Linear search)
선형 검색이란, 선형으로 나열되어 있는 데이터를 순차적으로 스캔하면서 원하는 값을 찾는 것을 말한다. 예를 들어 선형의 데이터, 정수형 데이터를 담은 리스트가 있다고 가정하자.
여기서 원하는 숫자를 찾아낸다고 할 때, 인덱스 0의 데이터부터 차례대로 마지막까지 하나씩 원하는 숫자를 찾아내는 방법을 말한다.
datas = [3, 2, 5, 7, 9, 1, 0, 8, 6, 4]
print(f'datas : {datas}')
print(f'length of datas: {len(datas)}')
searchData = int(input('찾으려는 숫자 입력: '))
searchResultIdx = -1
n = 0
while True:
if n == len(datas):
searchResultIdx = -1
break
elif datas[n] == searchData:
searchResultIdx = n
break
n += 1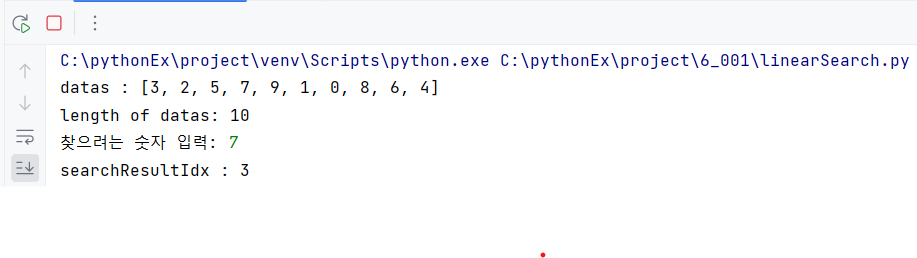
이때, 마지막 인덱스까지 도달하기 전에 리스트 안에서 원하는 데이터를 찾았다면, 탐색 과정을 중단하게 된다.
선형검색에는 찾고자 하는 데이터를 나열된 데이터열의 마지막 인덱스의 담아서 검색하는 '보초법'도 있다. 데이터의 인덱스를 구했을 때, 마지막 인덱스가 나오면 데이터가 없는 것이고, 그 이전에 나오면 데이터 검색에 성공한 것이다.
print(f'datas: {datas}')
searchData = int(input('찾으려는 숫자 입력: '))
searchResultIdx = -1
datas.append(searchData)
print(f'datas: {datas}')
n = 0
while True:
if datas[n] == searchData:
if n != len(datas) -1:
searchResultIdx = n
break
n += 1
print(f'searchResultIdx : {searchResultIdx}')
.
.
(2) 이진 검색(Binary search)
이진 검색이란, 데이터를 탐색할 때, 그 범위를 반씩 점차 좁혀서 탐색하는 것을 말한다. 리스트 형식의 데이터가 있다고 하자.(이때 데이터는 이미 정렬된 상태이다.) 리스트 중에서 가운데의 데이터가 찾는 데이터보다 작다면, 앞쪽의 1/2부분의 가운데의 데이터값과 크기 비교를 해서 찾는 데이터의 인덱스를 탐색하는 것이다.
datas = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
print(f'datas: {datas}')
searchData = int(input('찾으려는 숫자 입력: '))
searchResultIdx = -1
startIdx = 0
endIdx = len(datas) -1
midIdx = (startIdx + endIdx) // 2
midValue = datas[midIdx]
while searchData <= datas[len(datas) -1] and searchData >= datas[0]:
if searchData == datas[len(datas)-1]:
searchResultIdx = len(datas) -1
break
if searchData > midValue:
startIdx = midValue
midIdx = (startIdx + endIdx) // 2
midValue = datas[midIdx]
print(f'midIdx : {midIdx}')
print(f'midValue : {midValue}')
elif searchData < midValue:
endIdx = midIdx
midIdx = (startIdx + endIdx) // 2
midValue = datas[midIdx]
print(f'midIdx : {midIdx}')
print(f'midValue : {midValue}')
elif searchData == midValue:
searchResultIdx = midIdx
break
print(f'searchResultIdx: {searchResultIdx}')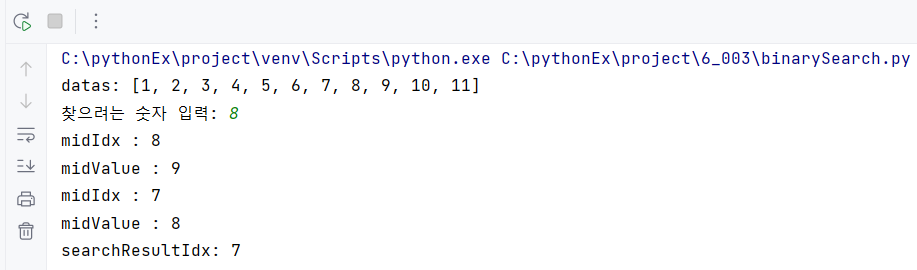
.
.
.
.
2. 순위 알고리즘
데이터들의 크기 비교를 해서, 순서를 매기는 것이다.
50부터 100까지 임의의 10개의 데이터가 저장된 리스트가 있다고 할 때, 맨 앞부터 하나씩 다음 순서와 비교해서 크기가 작다면 순위를 1씩 증가시키는 rank 리스트를 할당한다. 이렇게 해서 최종 순위리스트의 아이템들을 모두 1씩 더하면
가장 큰 데이터의 순위 데이터가 1, 가장 작은 데이터의 순위 데이터가 10이 저장되는 순위를 구할 수 있다.
import random
nums = random.sample(range(50,101),10)
ranks = [0 for i in range(10)]
print(f'ranks: {ranks}')
for idx, num1 in enumerate(nums):
for num2 in nums:
if num1 < num2:
ranks[idx] += 1
print(f'nums: {nums}')
print(f'ranks: {ranks}')
print('-'*90)
for idx, num in enumerate(nums):
print(f'num: {num} \t\t rank: {ranks[idx]+1}')
.
.
3. 정렬 알고리즘
(1) 버블정렬(bubble sort)
처음부터 끝까지 인접하는 인덱스의 값을 순차적으로 비교하면서 큰 숫자를 가장 끝으로 옮기는 알고리즘이다.
예를 들어, [10, 2, 7, 21, 0] 리스트 데이터를 버블 정렬하려고 한다.
[10, 2, 7, 21, 0]
10과 2를 비교해서 큰 수를 뒤로 보낸다.
[2, 10, 7, 21, 0]
다음 인덱스로 넘어가서 10과 7을 비교해서 큰 수를 뒤로 보낸다.
[2, 7, 10, 21, 0]
10과 21를 비교했으나 21이 크므로 다음 비교과정으로 넘긴다. 21과 0을 비교해서 큰 수를 뒤로 넘긴다.
[2, 7, 10, 0, 21]
이런 식으로 차례대로 정렬을 이어나가는 것이다.
nums = [10, 2, 7, 21, 0]
print(f'not sorted nums: {nums}')
length = len(nums) -1
for i in range(length):
for j in range(length -i):
if nums[j] > nums[j+1]:
nums[j], nums[j+1] = nums[j+1], nums[j] #서로의 값 바꾸기
print(nums)
print('-'*70)
print(f'sorted nums: {nums}')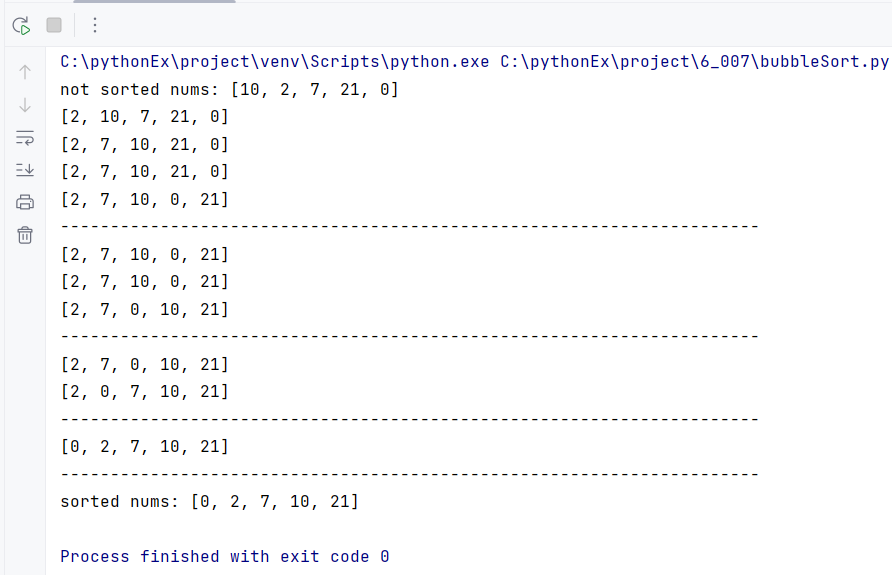
(2) 삽입정렬(insertion sort)
2번째 순서의 데이터부터 시작해서 한 단계씩 앞 인덱스와 크기 비교를 해서 본인의 자리에 끼워넣는 방식이다.
nums = [5, 10, 2, 1, 0] 리스트가 있다.
인덱스 1의 데이터 10부터 시작해서 앞 데이터와 비교. 5,10을 비교했으나 10은 5보다 크므로, 순서가 유효하다.
그대로 [5, 10, 2, 1, 0]이 된다.
인덱스 2의 데이터 2를 기준으로 먼저 10과 비교해서 본인의 자리를 찾는다.
[5, 2, 10 ,1, 0]
다시 한 단계 앞의 데이터 5와 비교한다. 2는 5보다 작다.
[2, 5, 10, 1, 0] 이 된다.
이런 식으로 앞 데이터와 비교하는 정렬 방법이다.
nums = [5, 10, 2, 1, 0]
for i1 in range(1, len(nums)): #2번쨰 순서부터 앞이랑 비교하면 됨
i2 = i1 -1 #앞순서. i1(뒷순서)랑 비교 목적
currentNum = nums[i1]
while nums[i2] > currentNum and i2 >= 0:
nums[i2+1] = nums[i2] #한단계씩 뒤로 밀려남
i2 -= 1
nums[i2 +1] = currentNum
print(f'nums: {nums}')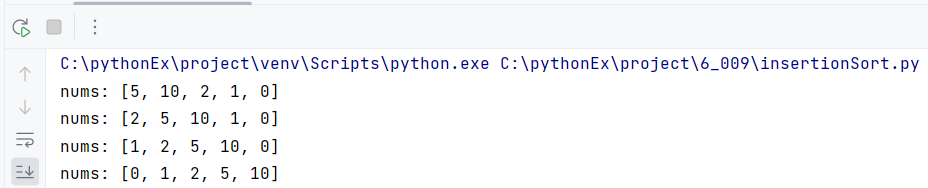
(3) 선택정렬(selection sort)
주어진 리스트 중에서 최솟값을 찾아, 그 값을 맨 앞에 위치한 값과 교체하는 방법이다.
nums = [4, 2, 5, 1, 3] 리스트가 있다.
인덱스 0을 기준으로 나머지 데이터들 중 최솟값을 찾는다. 최솟값(1)과 nums[0]을 비교했을 때, 최솟값이 더 작으므로 두 데이터의 순서를 교체한다.
nums = [1, 2, 5, 4, 3]이 되었다.
다음 인덱스 1을 기준으로 나머지 데이들 중 최솟값(3)과 비교했으나, nums[1]이 더 크기가 작으므로 순서를 교체할 필요 없다. nums[2]과 나머지 데이터들 중 최솟값(3)을 비교해서, 최솟값과 순서를 교체한다.
nums = [1, 2, 3, 4, 5]가 되었다.
nums[3]과 마지막 데이터 5를 비교했으나, 순서는 유효하다.
nums = [4, 2, 5, 1, 3]
for i in range(len(nums) -1):
minIdx = i
for j in range(i+1, len(nums)):
if nums[minIdx] > nums[j]:
minIdx = j
nums[i], nums[minIdx] = nums[minIdx], nums[i]
print(f'nums: {nums}')
print('-'*70)
print(f'final nums: {nums}')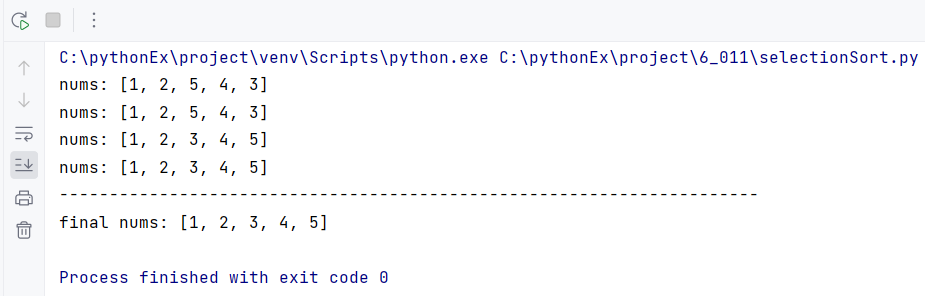
.
.
4. 최댓값 알고리즘
클래스를 만들어서 최댓값 구하는 알고리즘을 설정할 수 있다.
class MaxAlgorithm:
def __init__(self,ns):
self.nums = ns
self.maxNum = 0
def getMaxNum(self):
self.maxNum = self.nums[0]
for n in self.nums:
if self.maxNum < n:
self.maxNum = n
return self.maxNum
ma = MaxAlgorithm([-2, -4, 5, 7, 10, 0, 8, 20, -11])
maxNum = ma.getMaxNum()
print(f'maxNum: {maxNum}')
최댓값을 나열되어 있는 데이터의 가장 첫 번째 값으로 설정한 다음, 하나씩 다음 값과 비교한다. 초기 설정된 maxNum보다 제일 큰 값이 있다면 그 데이터가 최대값이 된다.

.
.
5. 최솟값 알고리즘
최댓값과 비슷한 과정으로 최솟값을 탐색하는 알고리즘을 구할 수 있다.
class MinAlgorithm:
def __init__(self,ns):
self.nums = ns
self.minNum = 0
def getMinNum(self):
self.minNum = self.nums[0]
for n in self.nums:
if self.minNum > n:
self.minNum = n
return self.minNum
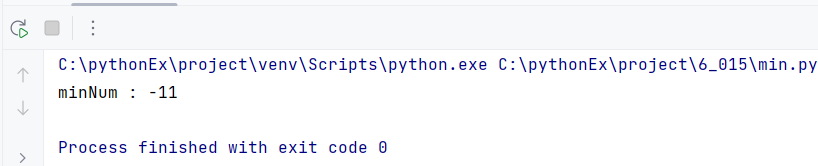
ma = MinAlgorithm([-2, -4, 5, 7, 10, 0, 8, 20, -11])
minNum = ma.getMinNum()
print(f'minNum : {minNum}')최솟값, minNum을 나열되어 있는 데이터의 가장 처음 데이터로 설정한다. 마찬가지로 하나씩 비교해서 가장 작은 값이 있다면 그 값이 최솟값이 된다.
.
.
6. 최빈값 알고리즘
최빈값은, 나열되어 있는 데이터들이 중복되어 있는 값을 포함한다고 할 때, 가장 많이 들어있는 값을 찾는 것이다.
앞에서 구한 최대값의 알고리즘을 활용해서 최빈값을 탐색할 수 있다.
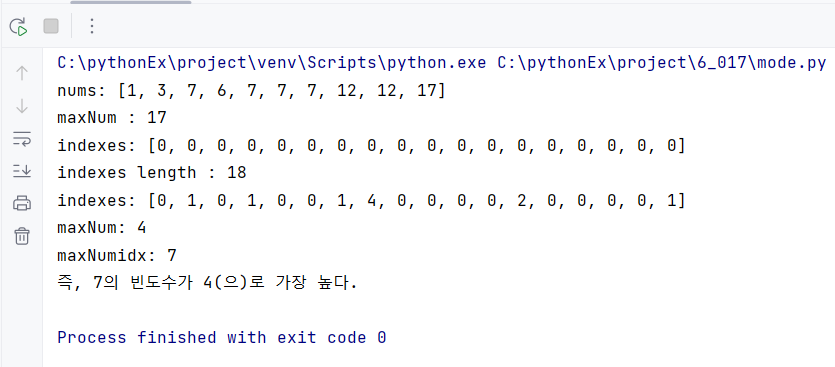
예를 들어, nums: [1, 3, 7, 6, 7, 7, 7, 12, 12, 17]의 리스트가 있다고 하자.
먼저 리스트 안에서 최댓값(17)을 찾는다.
이제 또 다른 리스트를 만든다. 이때, 최댓값의 인덱스만큼 0을 나열한다.
indexes: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
0을 인덱스가 17, 즉 총 18개가 든 리스트가 만들어졌다.
이제 nums에 나열된 아이템의 값들을 인덱스라고 가정한다.
예를 들어, nums안에 든 12을 indexes의 인덱스라고 하면 indexes[12]를 nums에 든 12의 개수만큼 1씩 할당한다.
그러면 indexes += 1을 총 두 번하게 돼서, indexes[12] = 2가 된다.
이러한 과정을 거치면,
indexes: [0, 1, 0, 1, 0, 0, 1, 4, 0, 0, 0, 0, 2, 0, 0, 0, 0, 1]
데이터를 만들 수 있다.
이때 가장 값이 큰 데이터의 인덱스가 nums의 최빈값이 된다. indexes[7]=4로 가장 크므로, nums의 최빈값은 7이다.
class MaxAlgorithm:
def __init__(self,ns):
self.nums = ns
self.maxNum = 0
self.maxNumIdx = 0
def setMaxIdxAndNum(self):
self.maxNum = self.nums[0]
self.maxNumIdx = 0
for i, n in enumerate(self.nums):
if self.maxNum < n:
self.maxNum = n
self.maxNumIdx = i
def getMaxNum(self):
return self.maxNum
def getMaxNumIdx(self):
return self.maxNumIdx
nums = [1, 3, 7, 6, 7, 7, 7, 12, 12, 17]
print(f'nums: {nums}')
ma = MaxAlgorithm(nums)
ma.setMaxIdxAndNum()
maxNum = ma.getMaxNum()
print(f'maxNum : {maxNum}')
indexes = [0 for i in range(maxNum+1)]
print(f'indexes: {indexes}')
print(f'indexes length : {len(indexes)}')
for n in nums:
indexes[n] += 1
print(f'indexes: {indexes}')
maxAlo = MaxAlgorithm(indexes)
maxAlo.setMaxIdxAndNum()
maxNum = maxAlo.getMaxNum()
maxNumIdx = maxAlo.getMaxNumIdx()
print(f'maxNum: {maxNum}')
print(f'maxNumidx: {maxNumIdx}')
print(f'즉, {maxNumIdx}의 빈도수가 {maxNum}(으)로 가장 높다.')