[014] 알고리즘 part2 / algorithm with python

Chapter
-Algorithm with python-
1. 근삿값 알고리즘
2. 평균 알고리즘
3. 재귀 알고리즘
(1) 재귀
(2) 하노이의 탑
(3) 병합 정렬
(4) 퀵 정렬

1. 근삿값 알고리즘

특정 값에 가장 가까운 값을 '근삿값'이라고 하며, 이를 찾아내기 위한 과정을
파이썬을 이용해서 풀어내겠다.

0~50 사이의 난수 20개를 이용한 예시로, 난수와 기준 값의 차이를 이용한다. 그 차이가 가장 작은 값(최솟값, minNum으로 설정함)이 근삿값이 된다.

import random

nums = random.sample(range(0,50), 20)
print(f'nums: { nums}')

inputNum = int(input('input number: '))
print(f'inputNum: {inputNum}')

nearNum = 0
minNum = 50

for n in nums:
    absNum = abs(n - inputNum)
    # print(f'absNum: {absNum}')

    if absNum < minNum:
        minNum = absNum
        nearNum = n
   

print(f'nearNum: {nearNum}')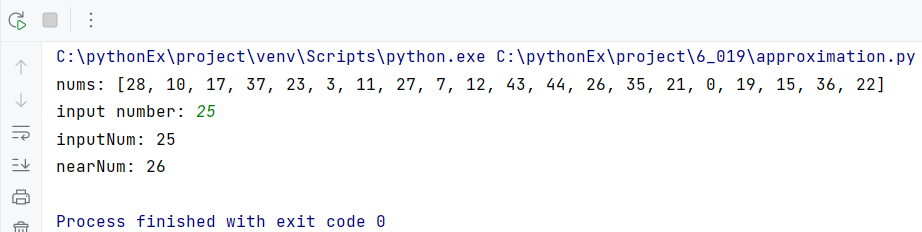

.
.
.
.

2. 평균 알고리즘

평균을 구하는 알고리즘을 파이썬을 이용해서 풀어낸다.

0~100사이의 난수 10개를 생성해서, 평균을 구하는 공식(값의 합/값의 갯수)를 이용해서 반복문을 돌린다.

import random

nums = random.sample(range(0,100), 10)
print(f'nums: {nums}')

total = 0
for n in nums:
    total += n

average = total / len(nums)
print(f'average: {average}')

위에서 구한 과정을 응용한다면, 특정 조건의 수들의 평균을 구할 수도 있다.
0~100사이의 난수 20개 중에서 50이상 90이하 수들의 평균을 구해보자.

# 50이상 90이하 수들의 평균
import random

nums = random.sample(range(0,100), 20)
print(f'nums: {nums}')

total = 0
targetNums = []
for n in nums:
    if n >= 50 and n <= 90:
        total += n
        targetNums.append(n)

average = total / len(targetNums)
print(f'targetNums: {targetNums}')
print(f'average: {round(average, 2)}')

.
.
.
.

3. 재귀 알고리즘

(1) 재귀함수

재귀함수란, 자기 자신의 함수를 다시 호출하는 것을 말한다.
두 가지 factorial과 유클리드 호제법의 예시를 들어 설명해보겠다.

- 'factorial'의 경우

팩토리얼은 자기 자신의 값부터 1씩 줄어들어 1이 되는 수 전부를 곱하는 값이다.
n! = n x (n-1) x (n -2) x ... x 1

def factorial(num):
    if num > 0:
        return num * factorial(num-1)
    else:
        return 1

print(f'factorial(5)= {factorial(5)}')

그러므로 함수를 정의할 때, num에서 그보다 1작은 num-1, 다시 1작은 num-2를 자신의 함수로 불러와서 모두 곱하게 한다. 이 때, 1!=1이므로 num=1이라면 1를 출력할 수 있도록 하는 것도 잊지 말하야 한다. (1x(1-1)=0이 되지 않게 하기 위해서)

.
.

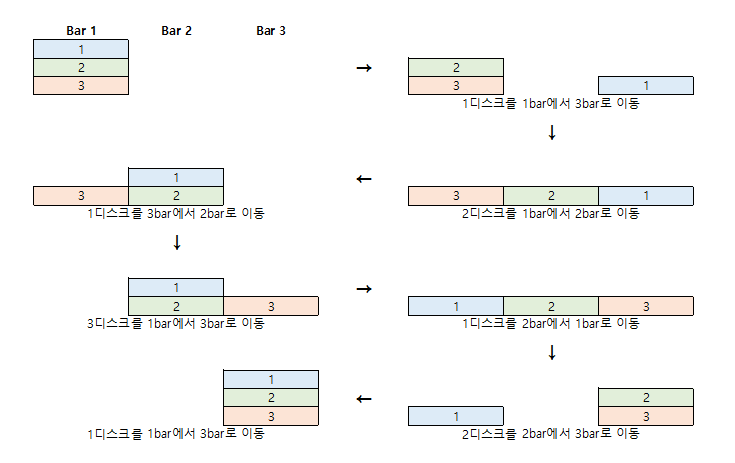
(2) 하노이의 탑

퍼즐 게임의 일종으로, 세 개의 기둥을 이용해서 원판을 다른 기둥으로 옮기는 것으로, 제약조건은 다음과 같다.

• 한 번에 한 개의 원판만 옮길 수 있다.
• 큰 원판이 작은 원판 위에 있어서는 안 된다.

과정을 살펴보면 아래의 그림과 같다.

이를 파이썬 코드로 나타내 보자.

# discCnt: 원판 개수
# fromBar: 출발 기둥 
# toBar  : 도착 기둥 
# viaBar : 경유 기둥

def moveDisc(discCnt, fromBar, toBar, viaBar):
    if discCnt == 1:
        print(f'{discCnt}disc를 {fromBar}에서 {toBar}(으)로 이동!')

    else:
        # (discCnt - 1)개들을 경유 기둥으로 이동
        moveDisc(discCnt-1, fromBar, viaBar, toBar)

        # discCnt를 목적 기둥으로 이동
        print(f'{discCnt}disc를 {fromBar}에서 {toBar}(으)로 이동!')

        # (discCnt-1)개들을 도착 기둥으로 이동
        moveDisc(discCnt-1, viaBar, toBar, fromBar)

moveDisc(3,1,3,2)

.
.

(3) 병합 정렬

자료구조를 분할하고, 각각의 분할된 자료구조를 정렬한 후 다시 병합하여 정렬하는 방식이다. 하나의 덩어리로 병합되어 있는 자료구조를 각각의 자료구조 길이가 1이 될 때까지 모두 잘게 자른다. 그 다음 원래의 자료구조의 길이만큼 점점 병합하면서 정렬하는 것을 말한다. (오름차순 기준)
nums = [8, 1, 4, 3, 2, 5, 10, 6] 리스트가 있다고 하자.
이를 점점 잘게 나누어서 각각 [8], [1], [4], [3], [2], [5], [10], [6]
의 구조로 병합한 다음 다시 크기 비교 정렬를 해서 [1, 8], [3, 4], [2, 5], [6, 10]의 형태로 병합한다.
다시 더 큰 구조로 병합 정렬을 해서 [1, 3, 4, 8], [2, 5, 6, 10]으로 정렬한다.
마무리 짓는다. [1, 2, 3, 4, 5, 6, 8, 10]

파이썬 코드를 이용해서 알고리즘을 나타내 보자.

def mSort(ns):

    if len(ns) < 2:
        return  ns

    # 분할 단계
    midIdx = len(ns) // 2
    leftNums = mSort(ns[0:midIdx])
    rightNums = mSort(ns[midIdx:len(ns)])

    # 병합 단계
    mergeNums = []
    lefIdx = 0; rightIdx = 0
    while lefIdx < len(leftNums) and rightIdx < len(rightNums):
        # 자리바꿈
        if leftNums[lefIdx] < rightNums[rightIdx]:
            mergeNums.append(leftNums[lefIdx])
            lefIdx += 1
        else:
            mergeNums.append(rightNums[rightIdx])
            rightIdx += 1

    mergeNums = mergeNums + leftNums[lefIdx:]
    mergeNums = mergeNums + rightNums[rightIdx:]

    return mergeNums


nums = [8, 1, 4, 3, 2, 5, 10, 6]
print(f'nums \t\t\t\t: {nums}')
print(f'nums by merge sort: {mSort(nums)}')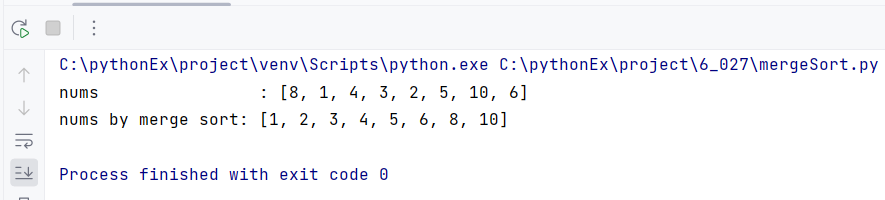

.
.

(4) 퀵 정렬

기준 값보다 작은 값과 큰 값으로 분리한 후 다시 합치는 과정이다.
nums = [8, 1, 2, 3, 4, 5, 4, 10, 6, 8] 리스트를 예로 들자.
nums의 가운데 인덱스 nums[4] = 4 의 값을 기준으로 잡는다.
그 다음, 4보다 작은 수 = [1, 2, 3], 같은 수 =[4, 4],
큰 수 = [5, 6, 8, 8, 10]으로 나눈 다음, 차례 대로, 작은 수부터 나열해서 다시 합친다.(오름차순 기준) [1, 2, 3, 4, 4, 5, 6, 8, 8, 10]

파이썬으로 코드를 나타내 보자.

def qSort(ns):

    if len(ns) < 2:
        return ns

    midIdx = len(ns) // 2
    midValue = ns[midIdx]

    smallNums = []; sameNums = []; bigNums = []

    for n in ns:
        if n < midValue:
            smallNums.append(n)
        elif n == midValue:
            sameNums.append(n)
        else:
            bigNums.append(n)

    return qSort(smallNums) + sameNums + qSort(bigNums)

nums = [8, 1, 2, 3, 4, 5, 4, 10, 6, 8]
print(f'not sorted nums: {nums}')
qSort(nums)
print(f'sorted nums: {qSort(nums)}')