스파르타 코딩클럽 데이터분석 4-2~3 선형 회귀란?

addison·2022년 3월 28일

2022.03

데이터 분석

목록 보기

34/48

4-2 선형 회귀 기초 및 분류의 차이

1) 선형 회귀란?

무언가를 예측할때
ex) 시험 공부하는 시간을 늘리면 늘릴 수록 성적이 잘 나옵니다. 하루에 걷는 횟수를 늘릴 수록, 몸무게는 줄어듭니다. 집의 평수가 클수록, 집의 매매 가격은 비쌉니다.

다른 변수의 값을 변하게하는 변수를 x, : 독립 변수
변수 x에 의해서 값이 종속적으로 변하는 변수 y : 종속 변수

y = wx + b

w를 머신 러닝에서는 가중치(weight),
별도로 더해지는 값 b를 편향(bias)
선형회귀란, 이런 식을 만들어서 w와 b의 값을 찾는 과정.

사실 상황에 따라서, 설명하는 방식에 따라서 이 용어는 다양합니다.
가령, b를 y절편이라고 부르기도하고, 단순히 상수(constant)라고 표현하기도 합니다.

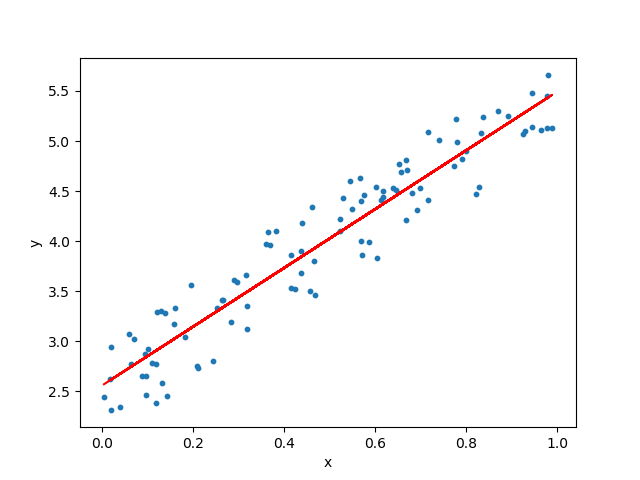
점이 데이터, 점에 가장 가깝게 선을 긋는 것.
선형 회귀? 선과 각각의 데이터들의 오차가 가장 적은 선을 찾는 것이 선형 회귀

2) 시험 성적으로 이해해보기

어떤 학생의 공부 시간에 따른 성적 데이터

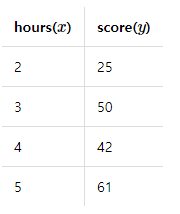
좌표 평면상 그리면,

y = wx + b

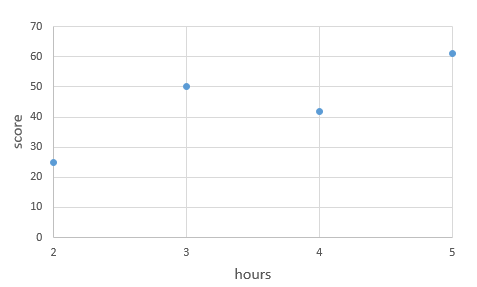
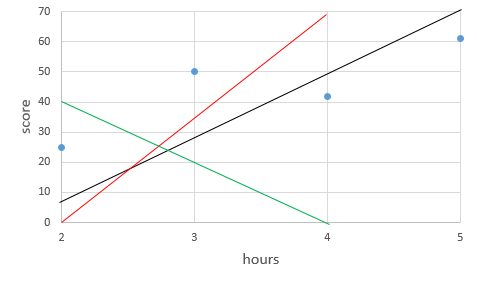
이중에 가장 잘 설명 하는 건 데이터들과 거리가 가장 적은 검은선.
이 검은선이 그래프 그림 밖으로 나가면 ? 한 6시간 공부하면 80점 정도 받겠네 라고 예측 가능

3) 다중 선형 회귀

y=w_{1}x_{1}+w_{2}x_{2}+...w_{n}x_{n}+b

단순 선형 회귀 : 한가지 요인만 결과에 요인 줄 때
다중 선형 회귀 : 다양한 요인이 작용할 때 (요인이 늘어난 만큼 가중치의 개수가 늘어남)

요인들 마다 각각의 가중치가 존재한다.

4) 회귀와 분류 개념의 차이

회귀라는건 위에서 본 것처럼, 성적/점수라는 특정한 수치를 추정하는 방식을 뜻합니다.

ex) 공부시간/학교와의 거리 등으로 성적을 예측하는 것, 집의 평수/방의 개수 등으로 집의 가격을 예측하는 것이 회귀입니다.

분류라는건 2주차 때 봤던 것처럼, 장르/감정 같은 특정한 범주/클래스를 추정하는 방식을 뜻합니다.

ex) 줄거리로 장르를 예측하는 것, 리뷰 내용으로 긍정/부정 여부를 예측하는 것이 분류입니다.

💡 회귀와 분류는 활용하는 머신러닝의 모델에서 차이가 나고, 사용할 수 있는 평가 지표에서도 차이가 납니다

회귀는 선형회귀, 릿지회귀, 라쏘회귀 등을 사용합니다.

분류는 로지스틱회귀 (말이 회귀일뿐 사실은 분류), SVM, 나이브베이즈분류기 등을 사용하게 됩니다.

평가 지표에서도, F1-Score/Precision/Recall 이라는 지표에 대해서 5주차에서 배우실텐데, 이러한 지표들은 모두 분류 에서만 사용할 수 있는 지표입니다.
ex) 예측한 장르랑 실제 장르랑 일치하는 데이터의 개수를 이용해서 정확도를 구했듯이, 예측값과 실제값의 일치 여부를 토대로 정확도를 구하게 됩니다.
반면에 회귀에서는 예측값과 실제 결과값의 오차를 토대로 정확도를 구하게 됩니다.
예측값이 실제값과 완전히 일치하기는 어려운 경우가 많으니, 오차가 가장 적은 모델을 좋은 모델이라고 평가하겠다는 것입니다.

💡 이러한 차이를 정확하게 이해를 하고 계셔야, 이후에 새로운 문제에 직면하게 되시더라도, 그 문제가 어떤 유형의 문제인지를 파악하고, 그 유형에 적합한 모델과 평가지표를 사용할 수 있을 것 입니다!

4-3 scikit-learn 패키지를 사용한 선형 회귀분석

5) scikit-learn 패키지를 사용한 선형 회귀분석

ex) 선형 회귀 실습 데이터
여러분들은 대학생입니다. 현재 중간 고사, 기말 고사, 가산점까지 모두 채점이 됐는데 최종 성적은 아직 나오지 않았습니다. 교수님께서는 매 학기마다 중간 고사, 기말 고사, 가산점을 바탕으로 어떤 공식을 통해 최종 성적을 결정한다고 하는데 이 공식은 밝혀지지 않았습니다.

지난 학기에 수강한 친구로부터 지난 학기 수강생들의 중간 고사, 기말 고사, 가산점과 최종 점수 파일을 전달받았습니다. 현 학기의 최종 성적이 공개되려면 2주나 남았는데, 여러분들은 최종 성적이 어떻게 나올지 너무 너무 궁금해서 미리 예측해보고 싶습니다. 지난 학기 데이터로 여러분들의 최종 성적을 미리 추론해볼까요?

y = w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+b

이 식이 나온 과정 : 중간이 몇퍼센트, 기말이 몇퍼센트, 가산점이 몇퍼센트, 보정치(b) 반영 비율이 궁금
if, x1이 중간고사 성적이면, w1 은 가중치(반영비율)가 된다.

import numpy as np
X = np.array([[70,85,11],[71,89,18],[50,80,20],[99,20,10],[50,10,10]]) # 중간, 기말, 가산점
y = np.array([73,82,72,57,34]) # 최종 성적

Q. 선형회귀를 어떻게 하느냐?

A. scikit-learn 패키지에, 선형 회귀분석을 하는 경우에는 linear_model 서브 패키지의 LinearRegression 클래스를 사용합니다. 사용법은 다음과 같습니다.

from sklearn.linear_model import LinearRegression

lr = LinearRegression() # 함수를 사용해서, lr라는 객체를 만들어야 쓸수있
lr.fit(X, y) # lr 이라는 객체,.fit은 시작이 되는 것. 이것을 학습이라 한다.

Q. 가중치와 편향값은 어떻게 구하는가?

A. 이제 coef_와 intercept_를 통해 학습 후의 가중치와 편향값을 출력할 수 있습니다.

# coef_에는 가중치들의 값이 담겨있다.
lr.coef_

array([0.38823654, 0.40424492, 0.98136214])

w_{1} = 0.38823654 \\ w_{2} = 0.40424492 \\ w_{3} = 0.98136214

# intercept_에는 편향의 값이 담겨있다.
lr.intercept_

->>

0.6960065780730318

b = 0.6960065780730318

💡 최종성적 = 0.38823654✖중간고사 성적 ➕ 0.40424492✖기말고사 성적 ➕ 0.98136214✖가산점 ➕ 0.6960065780730318

식이 완성된 것을 토대로 새로운 x1,x2,x3가 들어왔을 때 최종성적을 바로 알수있다.
그 과정을 predict() 함수를 통해서 알 수 있다.

new_data = [[60, 70, 80], [71, 90, 15]]
y_new = lr.predict(new_data)
y_new

array([130.79631462,  79.36327551])

위 수식에 근거하여 수작업으로 계산하면 다음과 같습니다.

lr.coef_[0]*60 + lr.coef_[1]*70  + lr.coef_[2]*80 + lr.intercept_

->>

130.79631462275842

addison

이전 포스트