데이터 분석 4-8 자전거 수요 예측 프로젝트(1) - MSE

addison·2022년 5월 1일

데이터 분석

목록 보기

35/48

👨‍🏫

평가지표 : 정확도를 계산하는 수단에 대해서 설명.

회귀같은 경우 평가할때 실제값과 에측값의 오차를 토대로 어떤 모델을 평가한다. 그 오차가 작을수록 좋은 모델이다. 그 오차 어떻게 계산하는 것인가.

1) `RMSLE` 구현하기

자전거 수요 예측 경진 대회의 주최 측에서는 모델의 성능을 예측하는 지표로 RMSLE(Root Mean Squared Log Error)를 사용했습니다. 회귀 문제에서 성능을 평가하기 위해 사용되는 여러 유명한 지표 중 하나입니다. RMSLE 외에도 MAE, MSE, RMSE 등 여러 회귀를 위한 지표들이 Kaggle과 기타 여러 논문들에서 RMSLE와 함께 쓰이고 있습니다.

여기서 회귀의 성능 지표로 사용할 RMSLE의 수식은 다음과 같습니다.

👨‍🏫 : 오차는 오차인데/ 로그가 취해져있고/ 제곱이 되어있고/ 평균으로 만들어져있고/ 루트가 씌워여 있는.
이름에 오차를 만드는 방식이 다 쓰여져있는데 되게 복잡하다.

어쨌든 오차를 계산하는 것.

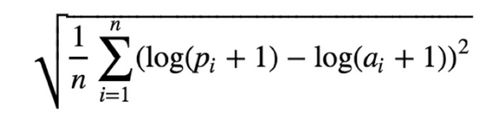
이때, 각 변수가 의미하는 바는 다음과 같습니다.

n : 데이터의\ 개수 \\ p_{i} : i번째 예측값 \\ a_{i} : i번째 실제값

식이 어려워보이지만 그냥 예측값 - 실제값 = 오차 라는 사실을 조금 복잡하게 표현한 것 뿐입니다!

예측값 에다가 로그를 취하고,
실제값 에다가 로그를 취한 뒤에,
둘을 빼서 오차값을 구한 것입니다.
그리고 그 오차값을 제곱하고,
그 오차값의 제곱이라는 값을 모든 데이터에 대해서 구해서 다 더한 뒤에, (다 더하는 것이 시그마의 역할)
데이터 갯수로 나누고 (모든 데이터에 대해서 오차값 제곱의 평균값을 구하는 것이죠!),
그 모든 데이터에 대한 오차값 제곱의 평균값에다가 루트를 씌워준 것입니다.

함수로 구현하면 (코드스니펫- 복사해서 써도 되는 코드)


def rmsle(y, pred):
		# y : 전체 데이터의 실제값의 리스트 ex) [1, 2, 3, 4]
		# pred : 전체 데이터의 예측값의 리스트 ex) [0.97, 1.85, 2.99, 3.87]
		
		# np.log1p : 입력값에 +1을 한 후 log를 씌운다.
    log_y = np.log1p(y)
    log_pred = np.log1p(pred)

		# 실제값과 예측값의의 차이의 제곱
    squared_error = (log_y - log_pred) ** 2

		# 모든 데이터에 대해 평균을 구한 후(np.mean())
		# 루트를 씌워준다(np.sqrt())
    rmsle = np.sqrt(np.mean(squared_error))
    return rmsle

👨‍🏫 다음시간에 선형회귀 구현하면서 본격적으로 사용할 것인데 일단은 원리를 이해하면 된다. 데이터 분석 하는데에 있어서 함수자체가 사실 중요한 것은 아님. 오차를 계산하는 것은 수단. 얼마나 잘 구현해서 함수 만드느냐가 중요한게 아님.

이러한 원리로 오차를 계산하고, 어떤 모델을 평가할수 있구나.

위 함수를 순차적으로 해석해봅시다. 실제값과 예측값이 들어오면 우선 두 개의 값 모두 np.log1p를 통해서 1을 더한 후에 로그를 씌워줍니다. 그 후 두 개의 값의 차이는 제곱이 되고, (파이썬에서는 **2를 하면 값에 제곱이 됩니다.) 들어온 전체 데이터의 개수에 대해서 평균을 낸 후에, 루트를 씌워주고 리턴합니다.

2) SMES(Root Mean Square Error)

이 대회의 평가 요소는 RMSLE 였지만, 이번 수업에서는 RMSLE(Root Mean Squared Log Error)와 거의 유사한 평가 지표인 거의 유사한 RMSE(Root Mean Square Error)도 같이 계산해보겠습니다. RMSE는 RMSLE와 함께 논문이나 기타 경진 대회에서 굉장히 많이 사용되는 수식입니다.

RMSLE의 이름에서 Log가 제거되었는데, 실제로 수식도 그렇습니다.

RMSE의 수식은 다음과 같습니다. (여기서 루트가 없는 경우를 MSE 라고 부릅니다!)

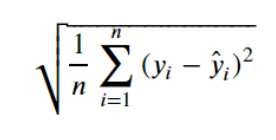
식이 어려워보이지만 마찬가지로 **예측값 - 실제값 = 오차** 라는 사실을 조금 복잡하게 표현한 것 뿐입니다!

예측값에서 실제값을 빼서 오차값을 구하고,
그 오차값을 제곱하고,
그 오차값의 제곱이라는 값을 모든 데이터에 대해서 구해서 다 더한 뒤에,
데이터 갯수로 나누고 (모든 데이터에 대해서 오차값 제곱의 평균값을 구하는 것이죠!),
그 모든 데이터에 대한 오차값 제곱의 평균값에다가 루트를 씌워준 것입니다.

RMSLE 와 다른 점은, 예측값, 실제값에다가 로그를 씌워주는 과정이 사라졌다는 것 뿐입니다!

👨‍🏫 원리 자체는 동일함

RMSLE도 직접 구현해볼 수도 있겠지만, MSE라는 또 다른 회귀 지표도 배워보는 차원에서

사이킷런에서 제공하는 MSE 함수를 임포트하고, 이를 이용하여 RMSE를 구현해봅시다.

👨‍🏫 원래라면 위와 같이 하나하나 구현해야 하지만, 사이킷런을 통해서 mean_squared_error 이 함수를 불러와서, 평가해볼 예측값과 실제값을 ()에 넣고 이 rmse라는 평가지표를 구해보는 것.

사이킷런에서는 MSE(Mean Squared Error)라는 회귀 분석의 성능 측정 지표를 제공하고 있는데, RMSE는 사실 MSE에서 루트를 씌워준 것뿐이므로 다음과 같이 구현합니다. (즉, 다시 말해 앞서 보여준 RMSE 수식에서 루트를 제거해주면 그것이 MSE입니다.)

RMSE 함수

from sklearn.metrics import mean_squared_error

def rmse(y, pred):
		# 평균 제곱 오차, MSE에 루트를 씌운다.
    return np.sqrt(mean_squared_error(y, pred))

코드를 보면 MSE에 루트만 씌웠습니다. 결과적으로 실습에서는 MSE에서 루트를 씌운 RMSE와 실제 대회상으로 평가지표였던 RMSLE로 성능을 측정해보겠습니다.

👨‍🏫 루트가 없는 걸 MSE 라고 하는데, 여기에 루트를 씌우면 RMSE가 된다. 여기에 로그를 취하면 RMSLE가 됨다.

앞으로의 실습을 위해 실제값과 예측값이 입력으로 들어오면

RMSE와 RMSLE를 동시에 출력하는 함수를 만들어둡니다.

👨‍🏫앞으로는 calculate_model_score(y, pred) 이 함수만 사용해서 어떤 모델을 만든 뒤에, 오차가 어떤 식으로 출력되는지 살펴볼 것이다. 그래서 그 오차값을 줄이기 위한 노력을 어떻게 할 수 있는지 아래에서 살펴볼 것이다.

[코드스니펫] < RMSLE, RMSE 둘 다 계산하는 함수 >

# RMSLE, RMSE 계산
def calculate_model_score(y, pred):
    rmsle_value = rmsle(y, pred)
    rmse_value = rmse(y, pred)
    print(f'RMSLE: {rmsle_value:.3f}, RMSE: {rmse_value:.3f}')

참고자료) 회귀의 다양한 성능 지표들

addison

다음 포스트

데이터 분석 4-8 자전거 수요 예측 프로젝트(1) - MSE