선형회귀분석

선형회귀분석이란 무엇인가

• 주어진 데이터를 가장 잘 설명하는 직선 하나를 찾는 것!
• 하나의 독립변수에 대한 선형회귀분석 -> 단순 선형 회귀
• 여러개의 독립변수에 대한 선형회귀분석 -> 다중 선형 회귀

손실 함수 및 경사하강법

손실함수

• 평균 제곱 오차 (MSE)는 예측한 값과 실제 데이터값의 차이를 제곱하여 평균을 냄
• 가중치 w 와 편차 b 쌍들을 비교하는 것이 가능
• 제곱 오차를 최소화 하는 w,b를 찾는 문제로 변환
  -> 오차는 예측값과 목푯값의 차이 -> 이를 손실함수(비용함수)로 나타냄.
  ->MSE를 손실함수(L2 손실함수)로 사용하여 w에 대한 오차를 나타냄
  -> 2차 함수를 푸는 문제로 최적의 w를 구하려면 시간복잡도가 O(n^3)으로 증가하여 많은 데이터를 사용하는 딥러닝 모델에서는 계산이 비효율적이며 확장성이 좋지 않음

경사하강법

• 손실함수에서의 비효율성과 바람직하지 못한 확장성으로 경사하강법을 사용한다.
• '경사(gradient)' 란 기울기로서 미분값을 의미한다.
• 주어진 w에서 경사를 구하고 지속적으로 w를 업데이트하여 오차의 극솟값을 찾을 수 있다.

파이토치에서의 경사하강법

그래프 정의

num_data = 1000 
num_epoch = 500


noise = init.normal_(torch.FloatTensor(num_data,1),std=0.2)
x = init.uniform_(torch.Tensor(num_data,1),-10,10)

# 연산 그래프 정의
y = 2*x+3

y_noise = y+noise

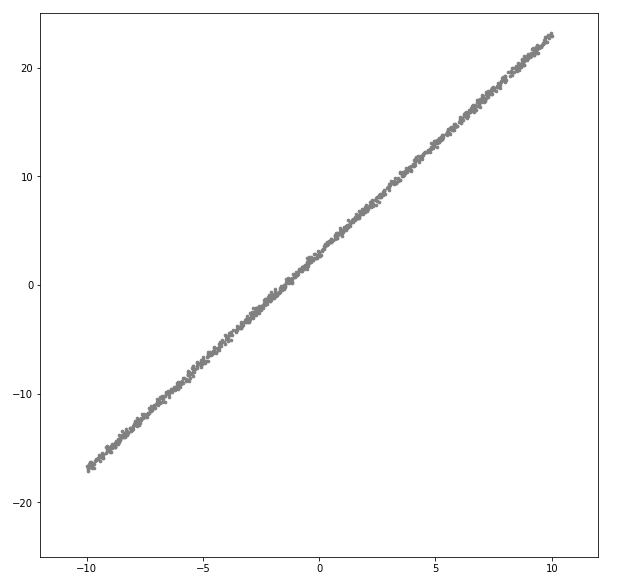
#데이터 시각화
plt.figure(figsize=(10,10))
plt.scatter(x.numpy(),y_noise.numpy(),s=7,c="gray")

plt.axis([-12, 12, -25, 25])
plt.show()

손실함수, 최적화 함수 설정

#모델 손실함수, 최적화 함수 설정
model = nn.Linear(1,1)

#손실함수
loss_func = nn.L1Loss()

#최적화 함수
optimizer = optim.SGD(model.parameters(),lr=0.01)

loss_arr =[]

label = y_noise

for i in range(num_epoch):

    optimizer.zero_grad()

    output = model(x)
    
    loss = loss_func(output,label)
 
    loss.backward()

    optimizer.step()
 
    if i % 10 == 0:
        plt.scatter(x.detach().numpy(),output.detach().numpy())
        plt.axis([-10, 10, -30, 30])
        plt.show()
        print(loss.data)
        
    # 손실을 loss_arr에 추가
    loss_arr.append(loss.detach().numpy())

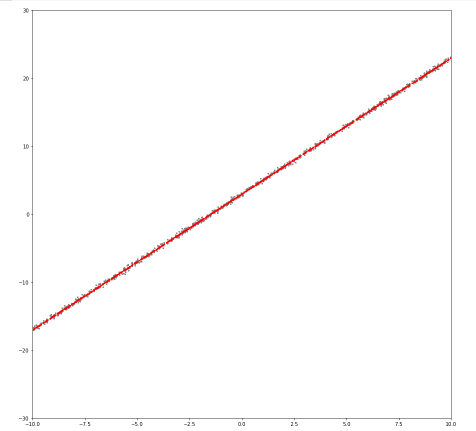
학습 후 데이터와 모델 결과값 확인

plt.figure(figsize=(15,15))
plt.scatter(x.numpy(),y_noise.numpy(),s=5,c="gray")
plt.scatter(x.detach().numpy(),output.detach().numpy(),s=5,c="red")
plt.axis([-10, 10, -30, 30])
plt.show()

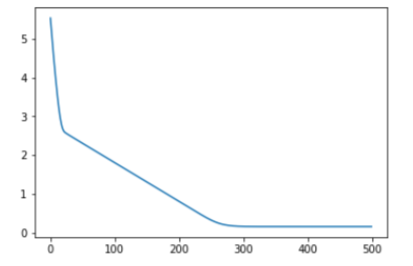
손실그래프 확인

plt.plot(loss_arr)
plt.show()

학습 후 모델 변수 값 확인

param_list = list(model.parameters())
print("Weight:",param_list[0].item(),"\nBias:  ",param_list[1].item())

• output :
  Weight: 2.001312017440796
  Bias: 2.98982834815979