Adaptivity without Compromise: A Momentumized, Adaptive, Dual Averaged Gradient Method for Stochastic Optimization

• 인공신경망 훈련은 반복계산과 역전파를 통한 gradent descent를 통해 모델을 최적화 해왔습니다. 기본적으로 너무 큰 계산 범위기 때문에 모델 최적화는 여러 어려움에 직면합니다. 이를 효율적으로 진행하기 위해 여러 방법이 개발되었는데, 근본중의 근본이 SGD를 거쳐 Adagrad 등 여러 방법론이 나왔고, Adam으로 정착되는 듯 했습니다.
• 최근 facebook AI Research 기존 Adam보다 뛰어나다고 주장하는 최적화 방법이 있다고 해 이 논문을 번역해보려 합니다. 물론 영어를 엄청 잘해서가 아니라, 번역기를 돌리고 어색한 부분을 수정하는 형태로 진행하려 합니다.
• 논문링크[link]
• 파이토치로 훈련할경우 모듈을 별도 설치 이후 바로 optimizer로 선언 가능합니다. (optimizer = madgrad.MADGRAD(model.parameters())) Github 링크[link]
• 저작권은 오롯이 논문의 원작자에게 있습니다.

Abstract

• 우리는 AdaGrad 적응형 그래디언트 방법의 계열에 속하는 새로운 최적화 방법인 MADGRAD를 소개합니다. MADGRAD는 비전의 분류 및 이미지-이미지 작업과 자연어 처리의 순환 및 양방향으로 마스킹된 모델을 포함하여 여러 분야의 딥러닝 최적화 문제에서 탁월한 성능을 보여줍니다. 이러한 작업 각각에 대해, MADGRAD는 테스트 세트 성능에서 SGD 및 ADAM을 매치하거나 능가합니다. 심지어 적응형 방법들이 일반적으로 성능이 떨어지는 문제에서도 마찬가지입니다.

1. Introduction

• 딥 러닝을 위한 최적화는 최적화 커뮤니티에서 비교적 새롭고 성장하는 하위 분야를 형성하고 있습니다. 기존의 1차 최적화와 비교하여 딥러닝 문제는 새로운 도구로 극복해야 하는 추가적인 문제를 야기합니다. 딥러닝 문제는 매개변수 벡터 크기가 매우 큰 것이 특징이며, 따라서 DXD 크기의 행렬을 저장하는 것은 계산적으로 불가능하며, 현재 연구 중인 1,000억 개 이상의 매개변수 모델과 같은 문제에는 "제한된 메모리" 접근 방식조차 비실용적일 수 있습니다. 이 문제들에 대한 실질적인 한계는 매개변수 벡터 크기의 소수 배에 고정된 저장 공간입니다.
• 이러한 이유로, 대각선 스케일링 접근법이 딥러닝 산업 표준이 되었습니다. 이 방법군의 방법에서는 각 좌표에 대해 적응이 독립적으로 수행되므로 메모리 사용량이 O(D)로 확장됩니다. 우리는 이 클래스에서 Adam을 벤치마크 방법으로 간주합니다. Adam은 광범위하게 채택되었으며, 일관되게 Adam을 능가하는 대체 적응형 방법은 없습니다.
• Adam은 대각 적응형 방법들의 풍부한 역사 위에 구축되었습니다. AdaGrad 방법은 전체 행렬 적응성 계획을 단순화하여 자연스럽게 도출되는 원칙적인 대각 적응성 접근법을 도입하였습니다. 이 접근법은 분명한 동기를 가지고 있으며, 볼록 손실에 대한 자연스러운 수렴률의 경계를 제공합니다. 이 방법군 내에서도 RMSProp 방법이 이 클래스에서 잘 작동하는 경험적 방법으로 등장했지만, 이론적 동기는 거의 없습니다. Adam 방법의 개발은 RMSProp에서 사용된 스케일링을 모멘텀의 형태를 포함시키고 최적화 초기 단계에서 적응성과 스텝 사이즈를 상당히 줄이는 안정화된 “편향 교정”을 추가함으로써 자연스러운 확장으로 볼 수 있습니다.
• Adam이 광범위한 성공을 거두었음에도 불구하고, 딥러닝 최적화를 위한 만병통치약은 아닙니다. Wilson et al. [2017]에 따르면 Adam과 다른 일반적인 적응형 최적화 방법들은 이미지 분류와 같은 중요한 문제들에서 나쁜 local minima으로 수렴한다고 합니다. 이것은 적응형 방법들이 일반적으로 잘 일반화되지 않는다는 일반적인 주장으로 이어졌습니다. 그러나 우리가 보여줄 것처럼, 이는 반드시 그런 것은 아닙니다. 우리가 이 작업에서 개발하는 방법은 적응성과 강력한 일반화 성능을 모두 갖고 있습니다.
• 우리의 MADGRAD(Momentumized, Adaptive, Dual averaged GRADient) 방법은 Adam보다 더 많은 튜닝 없이도 다양한 실제 대규모 딥러닝 문제들에 대해 일관되게 최첨단 수준의 성능을 발휘합니다. MADGRAD는 상대적으로 덜 사용되는 AdaGrad의 이중 평균화 형태에서 출발하여, 딥러닝 최적화에 맞게 방법을 조정하는 일련의 직접적이고 체계적인 변경을 통해 구축되었습니다.

2. Problem Setup

• 파라미터화된 함수를 최소화하는 것이 목표인 확률적 최적화 프레임워크를 고려합니다.

  $f(x)=\mathbb{E}_{\xi}[f(x, \xi)]$

• 여기서 $x \in \mathbb{R}^D$이고, 각각의 $\xi$는 고정된 알려진 분포에서 추출된 임의 변수입니다. 경험적 위험 최소화의 경우, $\xi$는 데이터 분포에서 추출된 데이터 포인트이며, 일반적으로 확률적 데이터 증강 절차에 의해 추가로 처리됩니다. 각 단계 $k$에서, 확률적 최적화 알고리즘은 $\xi_k$를 받고, 사전에 지정된 반복 $x_k$에 대해 $f\left(x_k, \xi_k\right)$와 $\nabla f\left(x_k, \xi_k\right)$에 접근할 수 있습니다.

3. Related Work

• 비볼록 최적화를 위한 적응형 방법들에 대한 이론은 아직 초기 단계에 있습니다. Adam에 대한 현재 알려진 최고의 수렴 이론은 Défossez et al. [2020]로 인해 크게 향상되었으나, $N$ 번의 반복에 대해 $\beta = 1 - \frac{1}{N}$ 순서의 모멘텀 값을 요구한다는 중요한 경고가 있습니다. 이는 실제로 사용되는 값인 $\beta = 0.9$에서 $\beta = 0.99$ 순서와는 거리가 멉니다. 이러한 설정에 대한 결과는 불가능할 수도 있으며, Reddi et al. [2018]은 볼록한 경우에도 일반적인 매개변수 설정 하에서 Adam이 수렴하지 못할 수 있음을 반례를 통해 보여주었습니다. $\beta_1$과 $\beta_2$가 작을 때, Adam 업데이트는 sign-sgd에 가깝습니다(즉, $x_{k+1} = x_k - \gamma \cdot \text{sign}(\nabla f(x_k, \xi_k))$), 이 방법 역시 일반적인 확률적 사례에서 수렴하지 못합니다 [Balles and Hennig, 2018]. 그러나 일부 이론은 비확률적 사례에 더 가까운 행동을 하는 큰 배치 가정 하에서 가능합니다 Bernstein et al. [2018].
• 비볼록 상황에서의 AdaGrad의 수렴성도 연구되었습니다. Ward et al. [2019]은 전역 스텝 크기만이 적응적으로 업데이트되는 제한된 변형에 대한 수렴성을 확립했습니다. Li와 Orabona [2019]은 분모에서 가장 최근에 본 그래디언트가 생략된 AdaGrad의 변형에 대한 거의 확실한 수렴성을 확립했습니다. 전역적이고 좌표별이 아닌 스텝 크기를 가진 변형에 대해서도 높은 확률로 수렴성이 확립되었습니다. 더 최근에 Zhou et al. [2020]과 Zou et al. [2019a]는 각각 비모멘텀과 모멘텀 변형의 수렴성을 확립했지만, Défossez et al. [2020]에 의해 확립된 것보다 훨씬 더 나쁜 경계를 가집니다. Défossez et al.는 그들의 분석에서 AdaGrad도 다룹니다.
• 이 연구에서 사용하는 가중치가 적용된 AdaGrad는 이전에도 여러 차례 탐구되었습니다. 비볼록 사례는 Zou et al. [2019a]의 연구에서, 볼록 사례는 Levy et al. [2018]의 연구에서 언급되었습니다. 가중치는 특히 강볼록 사례에서 흥미롭습니다. 여기서는 ${\lambda}_{k}\propto k^2$와 같은 가중치를 사용해 가속화된 수렴을 달성할 수 있습니다. 이 두 연구 모두 우리가 탐구하는 AdaGrad의 이중 평균화된 형태는 다루지 않습니다.

4. Adaptivity in deep learning beyond Adam

• MADGRAD 방법의 동기와 설계를 이해하기 위해서는 기존 방법들의 단점을 명확히 이해할 필요가 있습니다. 실제로 가장 널리 사용되는 적응형 방법인 Adam을 생각해보세요. Adam은 일부 중요한 문제들에서 놀라울 정도로 잘 작동하지만, 다음과 같은 문제들도 겪고 있습니다:

  • Adam은 ImageNet 트레이닝 문제를 포함하여 여러 중요한 상황에서 비적응형 SGD-M 방법에 비해 성능이 크게 떨어집니다.
  • 볼록한 설정에서조차 완전히 수렴하지 못하는 문제들이 구성될 수 있습니다.
  • 희소 그래디언트가 주어졌을 때, 사용되는 지수 이동 평균 업데이트는 비희소적이어서 희소 문제에 잘 맞지 않습니다.

• 이러한 문제들로 인해 Adam은 일반적인 딥러닝 최적화 도구의 목표에 정확히 도달하지 못합니다. MADGRAD 방법은 이러한 문제들을 직접적으로 해결하도록 설계되었습니다. MADGRAD는:
  • Adam이 일반적으로 사용되는 문제들에서 최첨단 성능을 달성하는 동시에, Adam이 일반적으로 성능이 떨어지는 문제들에서도 최첨단 성능을 달성합니다.
  • 볼록 문제에 대한 입증 가능하고 강력한 수렴 이론을 가지고 있습니다.
  • 모멘텀을 사용하지 않을 때 희소 문제에 직접 적용 가능합니다.

5. Design

• MADGRAD 방법은 딥러닝 최적화 문제에 적용될 때 AdaGrad 방법의 개별적인 단점들을 해결하는 여러 기술들의 결합입니다. 이미 알려진 수렴 이론을 가진 방법을 기반으로 구축함으로써, 우리는 Adam의 실용적인 성능 특성을 희생하지 않고도 여전히 입증 가능한 수렴성(볼록성 가정 하에)을 가진 방법을 구성할 수 있습니다. 우리는 이 기술들 각각을 차례로 상세히 설명하여, MADGRAD를 그 기초부터 구축해 나갈 것입니다.

5.1 Dual averaging for deep learning

• MADGRAD는 AdaGrad의 거울 하강(mirror descent) 형식이 아닌, 이중 평균화(dual averaging) 형식을 기반으로 합니다. AdaGrad에 대한 원래의 기념비적인 연구 [Duchi et al., 2011]에서는 거울 하강 형식과 동등한 가중치를 가진 이중 평균화 형식을 제시했지만, 딥러닝 최적화를 위해 이중 평균화 형식은 거의 사용되지 않았습니다. 주요 딥러닝 프레임워크(PyTorch, Tensorflow)에서 사용할 수 있는 AdaGrad 구현은 거울 하강 형식만을 포함하고 있습니다. 이것은 이중 평균화 형식에 대해 제시된 이론이 거울 하강 이론보다 더 우아하다는 주장에도 불구하고 그렇습니다. AdaGrad의 이중 평균화 형식은 다음과 같은 경계를 만족합니다:

  $\sum_{i=1}^k f\left(x_i\right)-f\left(x_*\right) \leq \frac{1}{\gamma} \psi_k\left(x_*\right)+\frac{\gamma}{2} \sum_{i=1}^k\left\|\nabla f_i\left(x_i\right)\right\|_{\psi_{i-1}^*}^2$

• 반면에 거울 하강 형식은 $\psi$의 브레그만 발산(Bregman divergence)을 포함하는 다음과 같이 더 복잡한 경계를 만족합니다:

  $\begin{gathered} \sum_{i=1}^k f\left(x_i\right)-f\left(x_*\right) \leq \\ \frac{1}{\gamma} B_{\psi_1}\left(x_*, x_1\right)+\frac{1}{\gamma} \sum_{i=1}^{k-1}\left[B_{\psi_{i+1}}\left(x_*, x_{i+1}\right)-B_{\psi_i}\left(x_*, x_{i+1}\right)\right]+\frac{\gamma}{2} \sum_{i=1}^k\left\|\nabla f_i\left(x_i\right)\right\|_{\psi_i^*}^2 . \end{gathered}$

• 이론적 간단함에서 분명한 장점이 있는데, 왜 이중 평균화 접근법이 더 널리 사용되지 않을까요? 이는 몇 가지 오해 때문이라고 생각합니다. 첫 번째 오해는 이중 평균화가 복합 최적화 상황에서만 흥미롭다고 여겨지며, 여기서는 희소성을 장려하거나 솔루션의 다른 속성을 유도하기 위해 정교한 정규화 기법이 사용된다는 것입니다. 매끄러운 비확률적 최적화의 경우, 경사 하강법과 거울 하강법은 (최적의 하이퍼파라미터 하에서) 일치합니다. 그러나 목적함수가 확률적이거나 비매끄러울 때, 이 방법들은 구별되고 실제로 매우 다른 행동을 보입니다.

• 이중 평균화는 주변 함수 $\psi$가 주어진 일반적인 형태를 가집니다:

  $\begin{aligned} g_k & =\nabla f\left(x_k, \xi_k\right), \\ s_{k+1} & =s_k+\lambda_k g_k, \\ x_{k+1} & =\arg \min _x\left\{\left\langle s_{k+1}, x\right\rangle+\beta_{k+1} \psi(x)\right\} . \end{aligned}$

• 그래디언트 버퍼 $s_0$은 제로 벡터로 초기화됩니다. 이중 평균화의 가장 간단한 형태는 표준 유클리드 제곱 노름이 사용될 때 발생합니다: $\psi(x) = \frac{1}{2} \|x - x_0\|^2$, 그리고 $\lambda_k = 1$인 경우, 이 방법은 다음과 같은 형태를 취합니다:

  $x_{k+1}=x_0-\frac{1}{\beta_{k+1}} \sum_{i=0}^k g_i .$

• 목적함수가 비매끄럽거나 확률적이거나 (또는 둘 다)일 경우, $\beta$ 수열의 형태가 $\beta_{k+1} = \sqrt{k+1}$이면 수렴하는 방법을 제공합니다. 비록 방정식 2가 쓰여진 대로 SGD와 별로 닮지 않았지만, SGD의 업데이트는 다음과 같습니다:

  $x_{k+1}=x_k-\gamma_k \nabla f\left(x_k, \xi_k\right),$

• SGD의 업데이트는 더 비교 가능한 형태로 작성될 수 있습니다:

  $x_{k+1}=x_0-\sum_{i=0}^k \gamma_i g_i .$

• 수렴을 달성하기 위해 고정된 정지 시간 없이 스텝 크기 형태 $\gamma_i \propto \frac{1}{\sqrt{i+1}}$를 사용하는 것이 표준입니다. 단계 $k$에서 SGD와 DA를 비교할 때, SGD가 사용하는 가중치 수열이 합계에서 새로운 $g_i$에 비해 이전 $g_i$에 더 작은 가중치를 두는 것이 분명해지며, 반면 DA가 사용하는 수열은 모든 $g_i$에 동일한 가중치를 둡니다. 이 차이는 추가적인 정규화나 비유클리드 근사 함수 없이도 DA 계열의 방법들이 실제로 SGD와 다르게 행동하는 이유를 이해하는 데 핵심입니다.

• 두 번째 오해는 이중 평균화 형태의 AdaGrad를 딥러닝 환경에 필요한 수정 사항을 고려하지 않고 구현할 때 생깁니다. 원래 제시된 알고리즘은 초기점을 원점 $x_0 = 0$으로 사용하고, 이차적이지만 원점을 중심으로 하는 근접 함수 $\psi_t(x) = \frac{1}{2} \langle x, H_t x \rangle$를 사용합니다. 신경망 훈련이 원점에서 초기화될 때 병리적인 행동을 보인다는 것은 잘 알려져 있으며, 따라서 이 알고리즘을 순진하게 사용하면 성능이 좋지 않습니다. 0을 중심으로 할 때, 우리는 경험적 성능의 심각한 저하와 발산 위험을 관찰했습니다. 대신, $x_0$을 중심으로 한 근접 함수를 사용해야 합니다:

  $\psi_t(x)=\frac{1}{2}\left\langle x-x_0, H_t\left(x-x_0\right)\right\rangle,$

• 훈련되는 네트워크에 대한 표준 관례를 따라 $x_0$의 초기화가 이루어져야 합니다.

5.2 Dual averaging generalizes well

• 이중 평균화 방법의 이론적 장점 외에도, 우리는 그것들이 더 나은 일반화 성능이라는 강력한 실용적 장점을 누리고 있다는 것을 관찰했습니다. 이중 평균화 기반 방법들은 내재된 정규화 형태를 포함하고 있으며, 우리는 이것이 그들의 좋은 일반화 성능에 기여하는 중요한 요소라고 믿습니다. 이를 확인하기 위해, 고전적인 이중 평균화 업데이트를 고려해 보세요:

  $x_{k+1}=x_0-\frac{1}{\sqrt{k+1}} \sum_{i=0}^k g_i,$

• 이 업데이트는 $x_0$에 대한 대체를 통해 SGD 업데이트에 더 가까운 형태로 작성될 수 있습니다:

  $\begin{aligned} x_{k+1} & =\left(x_k+\frac{1}{\sqrt{k}} \sum_{i=0}^{k-1} g_i\right)-\frac{1}{\sqrt{k+1}} \sum_{i=0}^k g_i, \\ & =x_k-\frac{1}{\sqrt{k+1}}\left[g_k-\left(\frac{\sqrt{k+1}}{\sqrt{k}}-1\right) \sum_{i=0}^{k-1} g_i\right], \\ & =x_k-\frac{1}{\sqrt{k+1}}\left[g_k+(\sqrt{k+1}-\sqrt{k})\left(x_k-x_0\right)\right] . \end{aligned}$

• $\sqrt{k+1} - \sqrt{k} \approx \frac{1}{2\sqrt{k+1}}$ 이므로, 이중 평균화의 행동은 스텝에 따라 달라지는 정규화자를 가진 SGD 단계와 유사합니다:

  $\frac{1}{4 \sqrt{k}}\left\|x_k-x_0\right\|^2$

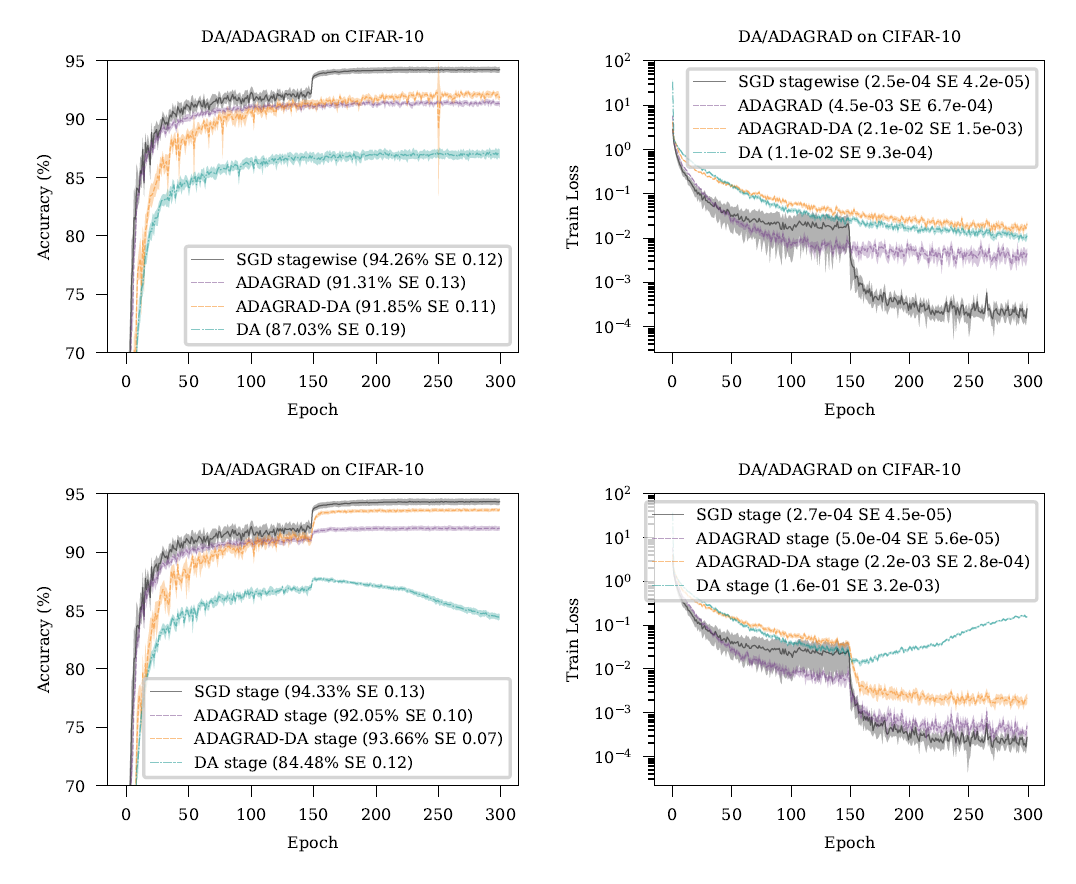
Figure 1: SGD(모멘텀 없음)와 DA, DA-AdaGrad, AdaGrad를 CIFAR-10 데이터셋에서 비교했습니다. 왼쪽 열은 테스트 분류 성능을, 오른쪽 열은 훈련 손실을 나타냅니다. "단계별" 학습률 계획은 150, 225 에포크에서 학습률을 10배 감소시키는 것을 포함합니다. 실험 설정에 대한 전체 설명은 섹션 7에서 확인하실 수 있습니다.

• 최적화 과정 동안 강도가 감소하는 정규화는, MADGRAD가 다른 방법들과 동등한 성능을 내기 위해 더 적은 감소를 요구하는 이유를 설명할 수 있습니다. 초기의 강력한 정규화는 초기 반복 동안 긍정적인 효과를 가져올 수 있으며, 나중의 "미세 조정(fine-tuning)" 에포크 동안 모델이 데이터에 적합해지는 능력에 부정적인 영향을 미치지 않습니다. 우리 실험에서 관찰한 실용적인 장점을 고려할 때, 최적화 초기 단계에서 더 강력한 정규화를 사용하는 효과에 대한 추가 연구가 일반적으로 흥미로울 수 있다고 믿습니다.

5.3 $\lambda$ sequences for deep learning

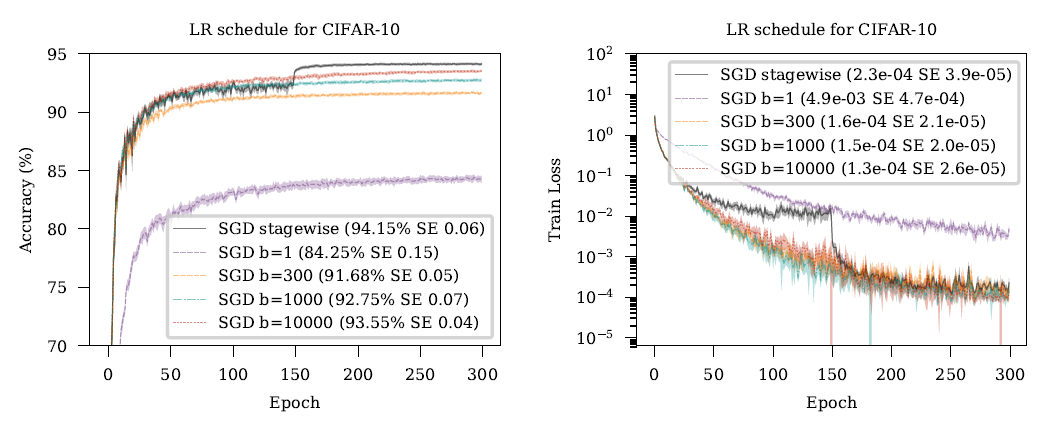
Figure 2: 제곱근 감소 학습률 일정은 단계별 일정에 비해 성능이 떨어집니다. 이 비교에서는 CIFAR-10에서 배치 크기 128과 모멘텀을 사용하지 않았습니다. $a / \sqrt{i+b}$의 비율에서 다양한 오프셋 $b$ 값이 시도되었으며, 최대 10,000까지의 값이 표시되었습니다. $b$의 더 큰 값인 100,000까지도 테스트되었지만, 그들 역시 단계별 일정의 성능에 미치지 못했습니다. 왼쪽 열은 테스트 분류 성능을 나타내고, 오른쪽 열은 훈련 손실을 나타냅니다.

• 이 수정을 가해도, CIFAR10과 같은 표준 벤치마크 문제에서 적응성이 있는 경우와 없는 경우 모두 이중 평균화는 SGD와 경쟁력이 없습니다. 그림 1에서 보여지듯이, 상단 행은 평탄한 학습률 일정을 사용하는 AdaGrad와 DA 방법을 보여주고, 하단 행은 단계별 일정을 보여줍니다. SGD는 기준선으로 표시됩니다. DA 계열 방법들에 대해, 단계별 일정에서는 $\lambda_k$가 감소됩니다. AdaGrad, DA 및 AdaGradDA 모두 학습률 일정이 어떠하든 SGD보다 성능이 떨어집니다. 이 성능 격차의 일부는 이러한 방법들이 암시적으로나 명시적으로 $1 / \sqrt{i+1}$ 학습률 수열을 사용하기 때문에 발생합니다. 이 수열은 사실 해로운데, 다음 형태의 일정을 사용하는 SGD를 테스트함으로써 확인할 수 있습니다:

  $\gamma_i=\frac{a}{\sqrt{i+b}}$

• 그림 2는 CIFAR-10에서 다양한 $b$ 값에 대해 달성 가능한 학습 곡선을 보여줍니다. 실험 설정에 대한 전체 설명은 섹션 7에 있습니다. 우리는 테스트 정확도를 목표 수량으로 하여 각각의 $b$에 대해 $a$를 별도로 하이퍼파라미터 검색을 수행했습니다. 모든 제곱근 감소 수열은 학습률이 에포크 150과 225에서 10배 감소하는 기준 단계별 일정보다 현저히 나쁩니다. 우리는 제곱근 감소 수열이 너무 빠르게 수렴하여, 학습의 초기 어닐링(annealing) 단계를 건너뛰고, 나쁜 지역 최소점으로의 수렴을 초래한다고 추측합니다. AdaGrad와 AdaGrad-DA 방법들 역시 암시적으로 감소하는 수열을 사용하지만, 감소 속도는 문제에 매우 의존적인 그래디언트의 크기에 따라 달라집니다. 만약 그래디언트가 특정 시간 척도에 걸쳐 비슷한 크기를 유지한다면, 감소율도 단계 $k$에 대해 $1 / \sqrt{k}$율이 될 것입니다. 이 스텝 사이즈 계획도 바람직하지 않으며, 명시적 스텝 사이즈 상수 $\lambda_i$를 선택하기 위한 표준 SGD 및 Adam 스텝 사이즈 수열의 사용을 방지합니다.

• 실제로 다른 최적화 방법을 비교할 때 일반적으로 동일한 학습률 계획이 사용되기 때문에, 이러한 일정은 AdaGrad가 Adam과 같은 다른 적응형 방법만큼 효과적이지 않다는 일반적인 인식에 기여합니다.

• DA 방법에 대해, 우리는 스텝 사이즈 수열의 영향을 상쇄하기 위해 $\lambda$ 값의 스케일링을 도입하여 이 문제를 해결할 것을 제안합니다. 특히 다음과 같은 선택을 제안합니다:

  $\lambda_i=(i+1)^{1 / 2} \gamma_i$

• 여기서 $\gamma$는 전통적인 (SGD/Adam) 스텝 사이즈 수열입니다. 이 선택의 장점은 식 2의 합계에서 주요 항이 $k$에 걸쳐 일정한 가중치를 갖게 됩니다:

  $\begin{aligned} x_{k+1} & =x_0-\frac{1}{\sqrt{k+1}} \sum_{i=0}^k \lambda_i g_i \\ & =x_0-\gamma_k g_k-\frac{1}{\sqrt{k+1}} \sum_{i=0}^{k-1} \lambda_i g_i. \end{aligned}$

• 이는 SGD가 일정한 스텝 사이즈 단계 동안의 행동을 반영하지만, 과거 그래디언트의 ( \sqrt{k+1} ) 감소는 유지합니다. 이 간단한 변경은 SGD와 동일한 학습률 일정을 사용할 때 DA의 테스트 세트 성능을 크게 향상시키기에 충분합니다.

• 이 수열의 또 다른 장점은 최종 수렴률 경계에서 나중의 그래디언트에 더 높은 가중치를 두게 됩니다. 이것은 최적화의 모든 단계에서 그래디언트가 비슷한 크기를 가질 것으로 예상한다면(비매끄러운 문제의 최악의 경우 발생할 수 있음) 차이가 없지만, 실제로는 비매끄러운 목적 함수라도 최적화 동안 그래디언트가 일정 정도 줄어들기 때문에, 전방 가중치 람다 수열을 사용할 때 더 타이트한 경계를 이끌어냅니다. 우리는 이 차이에 대해 섹션 6에서 더 자세히 논의합니다.

5.4 Momentum

• SGD 위에 모멘텀을 사용하는 것은 다양한 아키텍처와 문제 설정에서 딥러닝 최적화에 매우 유익하거나 필수적이라는 것이 알려져 있습니다(Sutskever et al., 2013). 경쟁력 있는 성능을 유지하는 데 얼마나 중요할 수 있는지 감안할 때, 이제 우리는 이중 평균화 업데이트와 이후 AdaGrad 업데이트에 모멘텀 형태를 추가하는 방법을 살펴보겠습니다.

• 우리는 다음 형태의 업데이트를 고려할 것입니다. 이것은 Nesterov와 Shikhman [2015]에 의해 '이중 평균화와 더블 평균화'라는 이름으로 이 일반적인 형태로 처음 탐구되었습니다:

  $\begin{aligned} g_k & =\nabla f\left(x_k, \xi_k\right), \\ s_{k+1} & =s_k+\lambda_k g_k, \\ z_{k+1} & =\arg \min _x\left\{\left\langle s_{k+1}, x\right\rangle+\beta_{k+1} \psi(x)\right\}, \\ x_{k+1} & =\left(1-c_{k+1}\right) x_k+c_{k+1} z_{k+1} . \end{aligned}$

• 이 알고리즘 뒤에 있는 핵심 아이디어는 간단합니다. 정규 DA와 같이 각 단계에서 argmin 연산의 값에서 그래디언트를 평가하는 대신, 이동 평균 지점에서 평가합니다. 이는 반복 수열을 부드럽게 만드는 역할을 합니다. 이 기술은 볼록 설정에서 평균 반복 $\bar{x}_{k+1} = \frac{1}{k+1} \sum_{i=0}^k x_i$ 대신 마지막 반복 $x_{k+1}$의 수렴 속성을 증명할 수 있게 하는 장점이 있습니다. 본질적으로 평균화 연산이 알고리즘 자체에 통합되어 있습니다.

• 모멘텀은 반복 수열의 단순한 부드럽게 만들기 이상의 역할을 하는 것으로 일반적으로 생각되지만, 최근의 연구 선상에서는 위와 같은 형태의 인라인 평균화가 실제로 모멘텀과 정확히 동일하다는 것이 밝혀졌습니다 [Sebbouh et al., 2020, Defazio, 2020]. 이는 SGD 위에 모멘텀이 추가될 때 인라인 평균화를 사용하면 명확하게 설명됩니다:

  $\begin{aligned} z_{k+1} & =z_k-\eta_k \nabla f\left(x_k, \xi_k\right), \\ x_{k+1} & =\left(1-c_{k+1}\right) x_k+c_{k+1} z_{k+1}, \end{aligned}$

• 사실, 보다 일반적인 모멘텀의 방정식 형태와 정확히 동일합니다:

  $\begin{aligned} m_{k+1} & =\beta_k m_k+\nabla f\left(x_k, \xi_k\right), \\ x_{k+1} & =x_k-\alpha_k m_{k+1}, \end{aligned}$

• 적절한 하이퍼파라미터 선택을 통해, 볼록한 환경에서는 $c_{k+1} = \frac{1}{k+1}$일 때 이 형태의 장점이 드러납니다. 이는 동등하게 가중된 이동 평균 $x_{k+1} = \frac{1}{k+1} \sum_{i=0}^k z_i$에 해당합니다. 이 설정 하에서는 마지막 반복의 수렴을 이중 평균화와 함께 이러한 종류의 평균화를 사용할 때와 마찬가지로 보여줄 수 있습니다 [Defazio and Gower, 2020]. 비볼록 설정에서는 지수 이동 평균에 해당하는 일정한 $c_{k+1}$ 값이 최선의 선택으로 보입니다 [Defazio, 2020].

5.5 Adaptivity

• 우리의 목표는 이러한 아이디어들을 AdaGrad 방법에서 온 적응성 기술과 결합하는 것입니다. 좌표별 AdaGrad의 이중 평균화 형태는 다음과 같은 형태를 가집니다:

  $x_{k+1}=x_0-\frac{1}{\sqrt{\sum_{i=0}^k \gamma_i g_i^2}} \circ \sum_{i=0}^k \gamma_i g_i,$

• 여기서 $\circ$는 원소별(아다마르) 곱셈을 나타내며, $\gamma$는 고정된 스텝 사이즈 하이퍼파라미터입니다. 우리가 제안한 가중치 그래디언트 수열 $\lambda_i = \sqrt{i+1}$과 이러한 종류의 좌표별 적응성을 결합하는 여러 가지 방법이 있습니다. 이중 평균화 프레임워크의 유연성으로 인해, 실질적으로 분모 수열의 어떤 선택에 대해서도 어떤 형태의 수렴률을 증명할 수 있습니다. 그러나, 우리는 또한 "효과적인" 스텝 사이즈의 크기를 유지하고 싶다는 점을 고려해야 합니다. 이는 섹션 5.3에서 논의되었습니다.

• 우리는 또한 가중 분모에 $\gamma_i$뿐만 아니라 $\sqrt{i+1}$도 포함되도록 해야 합니다. 이는 그림 1에서 DA에 대해 설명된 문제를 완화시키기 때문입니다: 에포크 150에서 $\lambda$가 10배 감소하면, 방법이 발산하기 시작합니다. 이 시점에서 $\beta$ 수열은 제곱근 속도로 계속 감소하는 반면, 그래디언트의 합은 10배 더 느리게 증가하기 시작합니다. 이로 인해 방법론은 반복값을 $x_0$ 쪽으로 너무 강하게 축소시키는 결과를 가져옵니다.

• 아래에서 몇 가지 가능한 대안들을 검토하고 그 실용성에 대해 논의하겠습니다.

5.5.1 UNWEIGHTED DENOMINATOR

• 한 가지 가능성은 분모를 동일하게 유지하되, 합계에서 그래디언트에 가중치를 부여하는 것입니다:

  $x_{k+1}=x_0-\frac{1}{\sqrt{\sum_{i=0}^k \gamma_i g_i^2}} \circ \sum_{i=0}^k(i+1)^{1 / 2} \gamma_i g_i$

• 이 방법은 일정한 효과적인 스텝 크기 속성을 유지하기 때문에 매력적이지만, 이 형태에서 유도할 수 있는 수렴 속도의 경계는 $\sqrt{\sum_{i=0}^k(i+1)^{1 / 2} \gamma_i g_i^2}$가 아니라 $\sqrt{\sum_{i=0}^k \gamma_i g_i^2}$에 의존하기 때문에 앞쪽 가중치가 있는 그래디언트 시퀀스를 사용하는 목적을 달성하지 못한다.

5.5.2 WEIGHTED DENOMINATOR

• 분모에서 그래디언트 수열에 $\lambda$로 가중치를 줄 수도 있습니다:

  $x_{k+1}=x_0-\frac{1}{\sqrt{\sum_{i=0}^k(i+1)^{1 / 2} \gamma_i g_i^2}} \circ \sum_{i=0}^k(i+1)^{1 / 2} \gamma_i g_i$

• 이 형태는 일정한 효과적인 스텝 사이즈를 유지하지 않으며, 이로 인해 경험적 성능이 좋지 않습니다. 성장을 상쇄하기 위해 분자에 추가 항을 더하는 것과 같은 완화 조치를 실험했지만, 여전히 만족스럽지 않은 경험적 결과를 가져왔습니다.

5.5.3 WEIGHTED NUMERATOR

• Zou et al. [2019a]가 제안한 AdaGrad 변형은 가중치 $\lambda_k$를 분자뿐만 아니라 분모에도 포함하는 가중치 계획을 사용합니다:

  $x_{k+1}=x_0-\frac{\gamma_i}{\sqrt{t}} \frac{\sqrt{\sum_{i=0}^k \lambda_i}}{\sqrt{\sum_{i=0}^k \lambda_i g_i^2}} \circ g_i=x_0-\frac{\gamma_i}{\sqrt{t}} \frac{\sqrt{\sum_{i=0}^k(i+1)^{1 / 2}}}{\sqrt{\sum_{i=0}^k(i+1)^{1 / 2} g_i^2}} \circ g_i \text {. }$

• 이 분자는 $t^{1/4}$에 비례합니다. 이 수열을 이중 평균화에 적용하기 위해, 우리는 가중치에 스텝 사이즈 매개변수를 포함시켜야 합니다. 효과적인 스텝 사이즈 특성을 유지하는 방식으로 이를 수행하는 방법은 명확하지 않습니다. 왜냐하면 $\lambda_i \propto \gamma_i$이면 분자와 분모 사이에서 스텝 사이즈가 상쇄되기 때문입니다.

5.5.4 MADGRAD's CUBE-ROOT DENOMINATOR

• 올바른 효과적인 스텝 사이즈를 유지하기 위해, 우리는 대신 세제곱근을 사용하는 것을 제안합니다:

  $x_{k+1}=x_0-\frac{1}{\sqrt[3]{\sum_{i=0}^k(i+1)^{1 / 2} \gamma_i g_i^2}} \circ \sum_{i=0}^k(i+1)^{1 / 2} \gamma_i g_i$

• 이 수정이 임시방편처럼 보일 수 있지만, 여기서 세제곱근을 사용하는 것은 표준 제곱근 형식을 동기 부여하는 데 사용되는 유사한 논리에 의해 실제로 설명될 수 있습니다.

• Duchi et al. [2011]은 $D$ 차원 벡터 $s$에 대한 다음 최소화 문제를 고려합니다:

  $\min _s \sum_{i=0}^k \sum_{d=0}^D \frac{g_{i d}^2}{s_d},\langle 1, s\rangle \leq c, \forall d: s_d>0,$

• 이 문제는 $s_d \propto \sqrt{\sum_{i=0}^k g_{i d}^2}$에 의해 해결됩니다. 이 대용 문제에 대한 동기는 사후적으로 그래디언트의 가중치가 부여된 제곱 노름을 최소화하는 것입니다. $s$의 크기에 대한 선형 페널티를 사용하는 대신, 양의 제약과 결합될 때 단순히 L1 노름 페널티 $\|s\|_1 \leq c$가 되는 것이 아니라, 대신 L2 노름 페널티를 사용한다면:

• 그러면 세제곱근 해결책 $s_d \propto \sqrt[3]{\sum_{i=0}^k g_{i d}^2}$를 얻게 됩니다. 이것은 부록에서 보여줍니다. 세제곱근은 $\sum_i^k(i+1)^{1 / 2} \propto (k+1)^{3 / 2}$를 고려할 때 효과적인 스텝 사이즈를 유지하는데, 세제곱근 연산 후에 필요한 $\sqrt{k+1}$으로 스케일링된 분모를 얻어 $\lambda$의 제곱근 성장을 상쇄시킬 수 있습니다.

• 이 가중치의 단점은 최종 수렴률 경계가 그래디언트 노름을 포함하는 식에 의존하는 전역 스텝 사이즈의 선택에서 완전히 적응적이지 않다는 점입니다. 그러나 함수의 부최적 간격과 그래디언트 경계 $G$와 같은 다른 알려지지 않은 양에 대한 스텝 사이즈의 선택이 완전히 적응적인 수열을 사용할 때조차 의존하는 점을 고려하면, 이것이 중대한 문제라고 생각하지 않습니다.

6. Convergence Theory

• 논의된 아이디어들을 결합한 MADGRAD 알고리즘은 알고리즘 1에 나열되어 있습니다. 비매끄러운 함수에 대한 수렴 결과를 확립하기 위해, 우리는 유계된 그래디언트 가정에 의존합니다:

  $\|\nabla f(x, \xi)\|_{\infty} \leq G \text { for all } x, \xi$

• 우리는 또한 각 $f(\cdot, \cdot)$가 모든 $\mathbb{R}^D$에 대해 $x$에서 적절하고 볼록하다고 가정합니다. 우리의 분석은 알고리즘 1의 약간 변형된 버전을 사용하는데, 여기서 분모에는 추가적인 항 $\lambda_k G^2$가 포함됩니다:

• 비슷한 용어는 Duchi et al. [2011]의 원래 DA-AdaGrad 방법에서도 필요하며, 축적된 오류를 제한하는 데 필요해 보입니다. 그러나 이 용어의 크기는 빠르게 줄어들기 때문에 실제로 중요한 역할을 한다고 생각하지 않으며, 그래서 알고리즘 1에 이 용어를 포함하지 않았습니다. 이론을 더욱 강화하기 위해 $G$ 대신 좌표별 상한 $G_d$를 사용할 수도 있습니다.

• Theorem 1. After $k$ steps of MADGRAD using the update in Equation 6,

• if $c_k=\frac{3 / 2}{k+3 / 2}$ and

• 이 경계는 매우 느슨합니다. 이는 각 시간 단계에서 그래디언트의 각 인덱스를 별도로 제한하기 위해 $\nabla f(x, \xi)_i \leq G$를 적용한 결과로, 수렴률의 적응성을 포착하지 못합니다. 더 정밀한 경계에 대해서는 아래에서 논의합니다. $\|g\|_2 \leq D^{1/2}\|g\|_{\infty} = GD^{1/2}$이므로, 여기서 차원성에 대한 의존성은 오른쪽에 그래디언트의 2-norm에 대한 경계를 가진 비적응적 확률적 방법들에 대해 확립된 경계와 비교할 수 있습니다. 또한 비볼록 문제에 대해서는 고정된 $c_k = c$ 모멘텀을 사용하는 것을 권장하는데, 이 감소율은 볼록한 경우에만 최적입니다. $c = 0.1$은 SGD와 Adam에서 흔히 사용되는 $\beta = 0.9$ 모멘텀에 해당합니다.

6.1 Adaptivity

• 메소드의 적응성을 더욱 세밀한 수준에서 이해하기 위해, 우리는 수렴 속도를 다음과 같이 표현할 수 있습니다:

• 수렴율은 가중치가 부여된 시퀀스에 크게 의존합니다:

• AdaGrad에서 사용되는 가중치 없는 합계 $\sum_{d=0}^{D} \sum_{i=0}^{k} g_{i d}^{2}$ 보다는 MADGRAD의 전통적인 AdaGrad에 대한 성능 특성을 이해하는 데 중요합니다. 특히,

• 초기 단계에서의 큰 기울기는 AdaGrad에 비해 전체적인 범위에 더 작은 영향을 미칩니다. 이는 기울기 범위가 시간에 따라 변화하는 경우, 즉 $\left\|\nabla f\left(x_{i}, \xi\right)\right\|_{\infty} \leq G_{i}$를 고려함으로써 정량화될 수 있습니다. 그리고 우리가 부록에서 보여주듯이, MADGRAD를 사용할 때 최적의 단계 크기를 사용하면:

• 모멘텀을 사용하는 AdaGrad의 경우:

• MADGRAD에서는 '이상치' $G_{i}$가 시간 단계 $i$에서 특히 큰 경우 AdaGrad에 비해 $5 / 4$의 거듭제곱으로 더 빠르게 감소합니다. 또한 우리의 모멘텀화 된 이중 평균화 기울기 프레임워크에서는 $1 / 2$보다 큰 거듭제곱을 가진 $\lambda_{i}$를 사용하는 것도 가능하며, 이는 더 빠른 감소를 초래합니다. 우리는 $1 / 2$ 요소가 '슈퍼-스팟'임을 발견했는데, 그 이상의 값은 경험적으로 더 느린 수렴을 초래합니다. 같은 증명 기술을 사용하여 비슷한 수렴률 경계를 도출할 수 있지만, 사용된 거듭제곱이 증가함에 따라 이들은 점진적으로 더 큰 상수(거듭제곱에서 계승으로 증가)에 의해 접두어가 붙게 됩니다. 일반적으로, 최적화 초기 단계에서 기울기가 가장 클 때, MADGRAD의 장점이 AdaGrad에 비해 드러납니다.

6.2 Comparison to Adam

• Adam이 이론적으로 발산할 수 있다고 알려져 있지만, 증명 가능한 수렴을 가져오는 Adam에 대한 가장 작은 수정사항으로 고려할 수 있는 AMSGrad 변형의 이론적 성질을 고려해볼 수 있습니다. AMSGrad의 경우, 단계 i에서의 모멘텀 $\beta_{1} \lambda^{i-1}$에 의해 매개변수화하고, 유한한 영역이 $R=\max _{x, y}\|x-y\|_{\infty}^{2}$로 가정하며, $\gamma=\beta_{1} / \sqrt{\beta_{2}}$를 정의하고, 스텝 사이즈 $\alpha_{i}=\alpha / \sqrt{i} \mid$ Reddi 등의 2018년에 사용합니다.

• $\hat{v}$는 제곱된 그래디언트의 지수 이동 평균의 최대치입니다, Reddi 외의 논문 (2018)을 참조하면 더 자세한 정보를 얻을 수 있습니다. 이 결과는 MADGRAD와 비교해서 여러 가지 단점이 있습니다. 우선, 모멘텀 항 $1-\beta_{1}$이 MADGRAD의 $c$와 비교해서 각 항을 나눈다는 걸 주목해주세요. 이것은 모멘텀이 성능을 향상시키기보다는 해치는 것을 의미합니다. 또한, 한정된 영역에 의존하는 것은 MADGRAD에 비해 불필요한 속성이기도 합니다. 그리고 MADGRAD의 수렴 이론은 로그 요인을 피합니다.

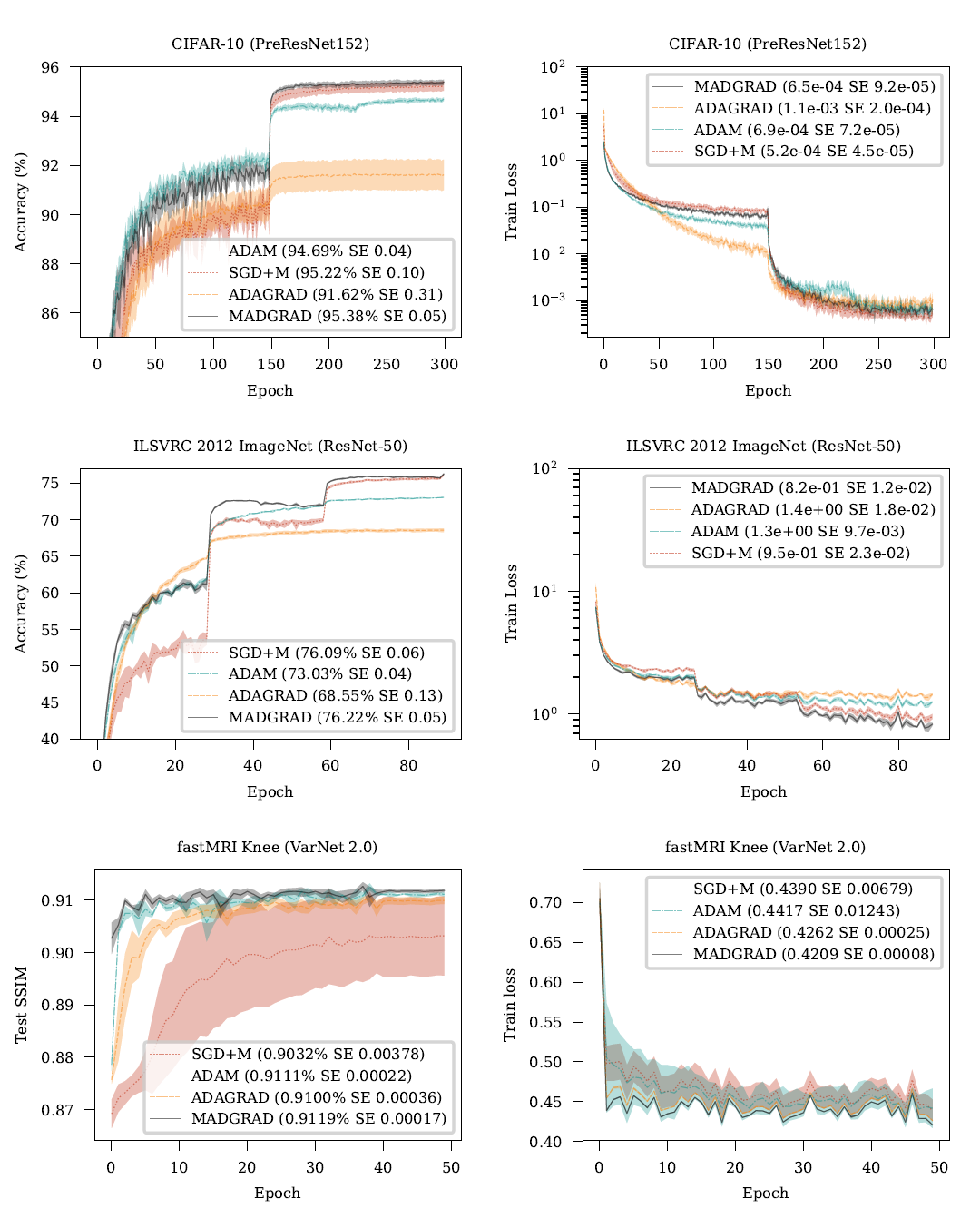
그림 3: CIFAR-10, ImageNet 그리고 fastMRI 무릎 문제에 대한 실험 결과. 왼쪽 열은 테스트 세트 성능을 보여주고, 오른쪽 열은 훈련 세트 성능을 보여줍니다.

7. Experimental Results

• 우리의 실험에서는 MADGRAD를 SGD, Adam, AdaGrad와 비교했습니다. SGD는 적응형 방법보다 일반화된 해결책을 제공하는 능력으로 인해 컴퓨터 비전 분류 문제에 잘 작동하는 것으로 알려져 있습니다. 반면에, Adam은 과적합이 덜 문제인 구조화된 출력을 가진 다른 영역에서 선택적인 방법입니다. 우리는 MADGRAD 접근법의 일반적인 유용성을 검증하기 위해 두 범주 모두의 많은 문제들에 대한 결과를 제시합니다.

• 우리의 실험에서는 각 해당 문제에 대해 문헌에서 가장 일반적으로 사용되는 단계 크기 축소 방식을 사용합니다. 모든 알고리즘들은, 각 문제와 방법에 대한 최적의 파라미터를 확보하기 위한 충분히 큰 범위의 $i$에 대해 $\left[1 \times 10^{i}, 2.5 \times 10^{i}, 5 \times 10^{i}\right]$ 간격의 그리드에서 학습률과 감소율을 조정했습니다. 우리는 테스트 세트 성능을 고려할 때 각 방법에 대한 최상의 학습률과 감소율의 결과를 제시합니다. 기타 하이퍼 파라미터에 관해서는 각 해당 문제에 대해 일반적으로 받아들여지는 기본값을 사용했습니다. 각 방법에 사용된 모든 파라미터 설정은 부록에 나열되어 있습니다. 제시된 모든 결과는 오차막대가 2 표준오차를 나타내는 여러 개의 시드에 대해 평균된 것입니다. CIFAR-10과 IWSLT14에는 10개의 시드가 사용되었지만, 나머지 더 큰 규모의 문제들에 대해서는 오직 5개의 시드만이 사용되었습니다.

7.1 CIFAR10 image classification

• CIFAR10 |Krizhevsky, 2009|는 그 크기가 적당하고, 데이터 제한이 있는 감독된 이미지 분류 문제의 성능을 대표하는 덕분에 딥러닝 커뮤니티 내에서 확립된 기준 방법입니다. 적응형 방법과 비적응형 방법 간의 명확한 차이를 보여주는 데 특히 주목할 만하며, 전자는 이 문제에서 상당히 과적합하는 경향이 있습니다. 표준적인 방법을 따라, 우리는 훈련시간에만 무작위 수평 반전, 4픽셀 패딩, 랜덤 크롭으로 이루어진 데이터 증가 단계를 적용합니다. 우리는 이 문제에서 잘 작동하는 것으로 알려진 고성능의 사전 활성화 ResNet 아키텍처 |He 등, 2016b|를 사용했으며, 이는 총 58,144,842개의 매개변수를 152개의 층에 걸쳐 구성됩니다. 이 네트워크의 깊이는 컴퓨터 비전 문제에 대한 네트워크 깊이의 전형적인 수익 감소 지점을 대표합니다. 이 네트워크는 크게 매개변수화되어 있으므로, 각 방법이 훈련 데이터를 정확하게 만족시킬 수 있으며, 심지어 이 데이터 증가에도 불구하고 거의 제로 손실을 달성할 것으로 예상됩니다. 이러한 이유로, 이 작업은 각 방법의 일반화 성능의 차이에 특히 민감합니다.

• 그림 3에서 보여지듯이, Adam과 AdaGrad 모두 이 문제에서 테스트 정확도 측면에서 성능이 좋지 않습니다. Adam의 이 문제에 대한 저성능은 잘 알려져 있습니다(Wilson 등, 2017), 그리고 일반적으로 초기의 훈련 세트 수렴이 매우 빠르기 때문에 불량한 지역 최솟값에 수렴한다는 것으로 설명되곤 합니다.

• MADGRAD은 이 문제에서 우수한 테스트 정확도 결과를 보여주며, 고려된 방법 중에서 가장 높은 테스트 정확도를 달성합니다. 이것은 Adam과 AdaGrad와 달리, MADGRAD의 적응성이 더 나쁜 일반화 성능의 비용으로 이루어지지 않음을 보여줍니다.

7.2 ILSVRC 2012 ImageNet image classification

• ImageNet 문제 |Krizhevsky 외, 2012|는 산업용 응용 프로그램에서 마주치게 되는 이미지 분류 문제를 더 잘 대표하는 더 큰 문제입니다. 여기서는 클래스 수가 많고 입력 이미지의 해상도가 높습니다. CIFAR10과 마찬가지로, 이 문제에서는 적응형 방법에서 과적합이 문제가 될 수 있습니다. 우리는 ResNet-50 아키텍처를 사용하여 실험을 진행했는데, 이것은 이 문제에 대한 표준 기준으로 간주됩니다. 이 데이터 세트와 아키텍처의 조합은 기계 학습 전반에서 가장 많이 연구된 것 중 하나로, 이는 최적화 알고리즘에 대한 이상적인 시험대를 만듭니다.

• 우리의 설정은 평균 $[0.485,0.456,0.406]$ 및 표준 편차 $[0.229,0.224,0.225]$의 정규화를 통한 데이터 전처리와 세 가지 색상 채널을 사용했습니다. 이후에는 PyTorch의 RandomResizedCrop 작업을 사용하여 해상도를 224 픽셀로 줄이고, 그 다음에는 가로로 뒤집을 확률이 $50 \%$ 인 무작위 작업을 수행했습니다. 테스트 세트 평가에는 256 픽셀로 크기를 조정한 후 중앙에서 224 픽셀로 자르는 것이 사용됩니다. 이 설정은 PyTorch 커뮤니티에서 표준으로 사용되지만, He 등의 설정과는 다르기 때문에 |2016a|, 즉, 테스트 정확도는 가깝지만 직접 비교할 수는 없습니다

• 이 문제에서 Adam과 AdaGrad는 CIFAR-10 문제에서 본 것과 유사한 수렴 속성을 보여줍니다. 그들 둘 다 모멘텀이 있는 SGD에 비해 훨씬 성능이 떨어집니다. MADGRAD는 여기에서도 강력한 성능을 보여주며, 대부분의 훈련 시간 동안 다른 어떤 방법보다 높은 테스트 정확도를 달성하고, 최종적으로는 가장 높은 테스트 정확도를 보여줍니다. MADGRAD의 에폭 70에서의 정확도는 75.87로, 이는 에폭 90에서 학습률이 감소한 후에 SGD $+\mathrm{M}$에 의해 달성됩니다. 이것은 28% 이상 더 긴 시간입니다. MADGRAD는 이 문제에서 훈련 손실에 대해서도 가장 좋은 성과를 보여줍니다.

7.3 fastMRI challenge MRI reconstruction

• fastMRI 무릎 챌린지 |Zbontar 등, 2018|는 최근에 제안된 대규모 이미지2이미지 문제입니다. 이전에 탐색된 분류 문제와 달리, 이 문제의 규모는 현재 최대 모델들의 가중치 수에 비추어 볼 때 과적합이 문제가 되지 않게 합니다. 이는 현재 소프트웨어 환경에서 훈련 가능한 모델들이 과적합에 취약하지 않다는 것을 의미합니다. 또한 이 문제는 이미지 처리 문제 중에서도 조건이 좋지 않다는 점에서 특히 주목할 만 합니다. 조건이 좋지 않은 이유 중 일부는 현재 SOTA 모델인 VarNet 2.0 Sriram 등 $|2020|$ 모델과 같은 현재의 깊은 모델 때문입니다. 이 모델은 총 273개의 계층에서 12,931,532개의 매개변수를 가지고 있습니다. 우리의 구현은 16개의 자동 보정 라인과 일정한 간격의 샘플링 패턴 |Defazio, 2019|을 사용하며, 이는 챌린지의 무작위 샘플링 마스크보다 실제의 임상 배치와 훨씬 가깝습니다.

• 그림 3은 이러한 방법들의 여러 가지 흥미로운 특성을 보여줍니다. SGD + M은 이 문제에 대한 성능이 매우 변동이 심하며, 다른 방법들에 비해 큰 차이로 성능이 떨어집니다. AdaGrad 역시 최고 성능을 내는 방법들, MADGRAD와 Adam에 비해 성능 격차가 명확합니다. MADGRAD는 최고의 성능을 보이며, 이 문제에 대한 표준 방법인 Adam에 비해 작지만 통계적으로 유의미한 향상을 보입니다. 훈련 셋의 성능은 변동성이 훨씬 높아 비교가 어려우나, MADGRAD가 훈련 손실에서도 가장 우수한 성능을 보이는 방법으로 보입니다.

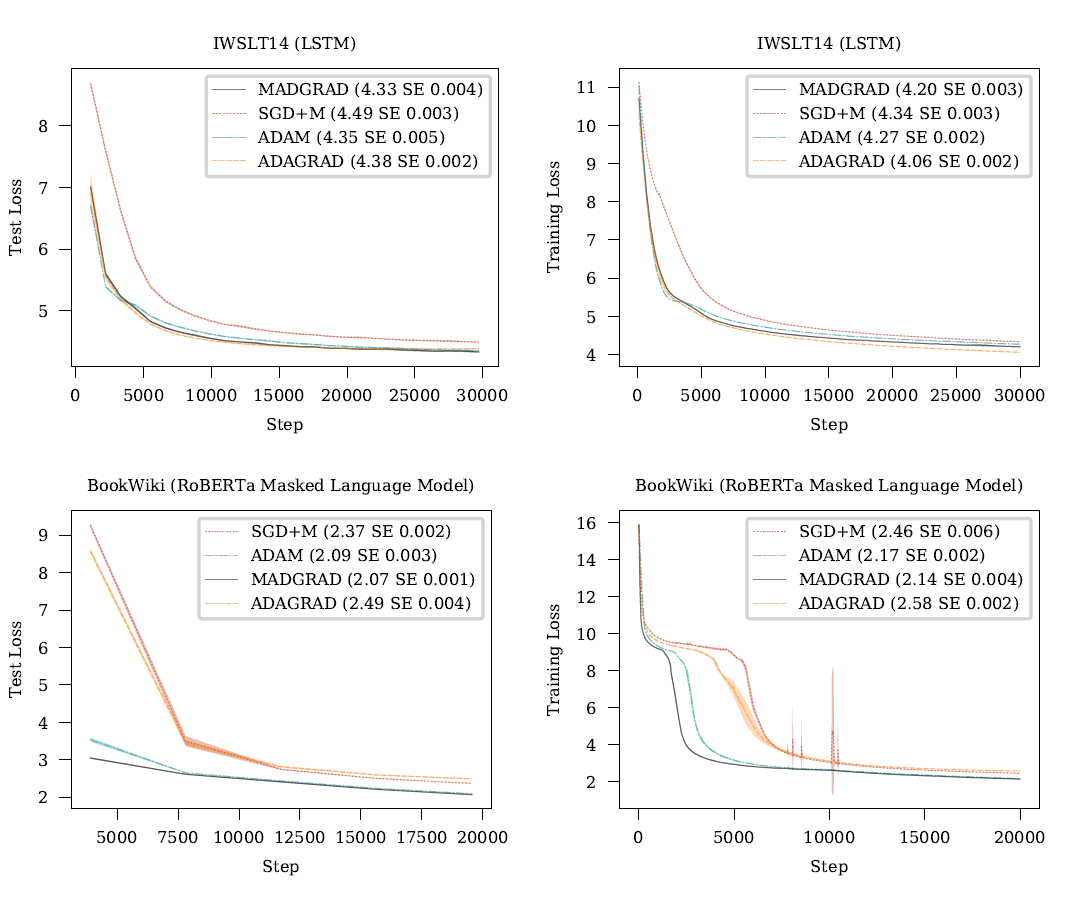
그림 4: IWSLT14와 BookWiki 문제에 대한 실험 결과입니다. 왼쪽 열은 테스트 세트 성능을 보여주고 오른쪽 열은 훈련 세트 성능을 보여줍니다.

7.4 Machine translation with a recurrent neural network

• 기계 번역 기준을 위해 우리는 우리의 모델을 IWSLT14 Germain에서 English 데이터셋에 대해 훈련시켰습니다 |Cettolo 등, 2014|, Wiseman과 Rush $|2016|$에 의해 소개된 인기 있는 LSTM 변형을 사용하였습니다.

• 그림 4는 모든 적응형 방법들이 이 문제에서 SGD를 상당한 차이로 능가함을 보여줍니다. 결과는 비슷하지만, MADGRAD가 약간의 성능 우위를 보이며, 테스트 손실은 4.33을 기록했고, AdaGrad는 4.38, Adam은 4.35였습니다. 훈련 손실에서 AdaGrad가 다른 방법들에 비해 앞선 것은 과적합의 약간의 정도 때문으로 볼 수 있습니다; AdaGrad는 최적화 끝부분에서 테스트 손실이 약간 증가하는 것을 보여줍니다, 이것이 이를 시사합니다.

7.5 Masked language modeling with a Transformer

• BERT 접근법에서 사용된 양방향 학습 목표는 자연 언어 모델의 대규모 사전 학습에 대한 새로운 표준으로 빠르게 자리 잡았습니다. 우리는 BERT_BASE의 RoBERTa 변형을 사용하여 실험을 수행했습니다. 이 모델은 110M 파라미터 트랜스포머 모델입니다. 이 모델은 대규모 트랜스포머 모델에 대한 현실적인 최적화 테스트 베드를 제공하는 충분히 큰 모델이면서도 ImageNet에서의 ResNet-50 모델처럼 학습 가능한 시간으로 학습할 수 있습니다.

• LSTM 문제와 유사하게, SGD + M은 이곳에서 성능이 떨어집니다. 훈련 손실이 급격히 악화되고 빠르게 회복하는 몇몇 피크를 보여줍니다. Adam과 MADGRAD 모두 잘 작동하지만, 처음에는 MADGRAD가 훨씬 빠르며, 또한 Adam이 달성한 2.09에 비해 2.07의 더 나은 최종 테스트 손실을 달성합니다.

8. Discussion

8.1 Hyper-parameter settings

• 우리는 실험 중에 다음과 같은 관찰을 하였습니다:

  • 일반적으로 이전 SGD/Adam 훈련에서 사용한 기본 가중치 감소를 사용하면 일반화 성능이 떨어집니다. 좋은 성능을 위해서는 가중치 감소가 훨씬 더 적거나 심지어 0이어야 합니다. 우리는 학습률 튜닝 전에 가중치 감소를 줄이는 것을 권장합니다.
  • 학습률 값은 SGD/Adam과 직접 비교할 수 없으며, 최적의 값을 찾기 위해서는 전체 학습률 스윕이 필요합니다. 별첨에서는 각 테스트 문제에 대한 최적의 학습률 값을 나열하였는데, 이는 좋은 시작점이 될 것입니다. 2의 거듭제곱 그리드를 통해 스윕하는 것이 권장되며, 이 값은 SGD/Adam과 수십 배 에 달하는 차이를 보입니다.
  • SGD/Adam에 사용되는 모멘텀 값은 문제 없이 작동해야 하며, 이는 모멘텀 $\beta$에 대해 $c=1-\beta$를 설정함으로써 가능합니다.

8.2 Empirical results in deep learning

• 우리는 우리의 실험적 검증이 새롭게 제안된 딥러닝 최적화 방법 중 가장 종합적으로 수행된 것 중 하나라고 믿습니다. 그리드 검색과 최종 평가를 수행하기 위해 GPU 사용 시간이 20,000시간 이상 필요했으며, 이는 우리가 MADGRAD 방법만이 아닌 고려된 각 방법에 대한 검색을 수행했기 때문입니다. 이는 하이퍼파라미터 최적화가 아니라 실제 성능 우위 때문에 우리의 방법이 그렇지 않으면 보일 것보다 좋아 보이는 것을 방지합니다. 우리의 비교는 또한 모던 딥러닝에 비해 소규모 문제보다 대형 및 실제 문제 수가 많이 포함되어 있습니다. 마지막으로, 최종 결과는 실행간 변동이 실제 성능 차이로 오해되지 않도록 각 문제에 대해 충분히 많은 수의 시드로 평균화됩니다. 이는 특히 CIFAR-10에서 문제되지만, 많은 출판 결과는 여전히 그 문제에 대한 비교를 위해 단일 시드만 사용합니다. 이런 이유로, 우리는 MADGRAD에 대한 우리의 실험 결과가 현대 대규모 실증적 위험 최소화 문제에서의 방법의 성능을 대표한다고 믿습니다.

8.3 Sparsity

• Adam 방법 내에서 제곱된 기울기에 대한 천천히 업데이트되는 이동 평균에 의존하는 것은 희소 모델에의 적용을 크게 방해합니다. 반대로, MADGRAD는 희소한 방식으로 업데이트 될 수 있는 제곱된 기울기 항목의 단순한 합을 유지합니다. 희소한 경우의 잠재적인 문제점은 반복자(기울기가 아닌)의 버퍼가 이동 평균으로 유지된다는 것입니다. 희소한 응용 프로그램을 지원하기 위해, 반복자 버퍼를 제거할 수 있으며, 이는 실질적으로 $c=1$을 설정하는 것과 동일합니다.

9. Conclusion

• 우리는 MADGRAD (모멘텀화된, 적응형, 이중 평균화된 경사하강) 방법을 딥러닝을 위한 일반적인 목적의 최적화 도구로 제안했습니다. MADGRAD의 최고 수준의 실증 성능과 강력한 이론적 기반을 고려할 때, 이것은 기계 학습의 많은 하위 분야에서 최적의 첫 번째 선택입니다.