번역: 머신러닝을 위한 수학

• 머신러닝을 이해하기 위해서는 많은 수학적 지식이 필요합니다.
• 단순히 코드만 사용해서 쓸 수도 있지만 좀더 깊이 있는 응용을 위해서는 벡터공간에 대한 이해가 필요합니다. 이를 위해 머신러닝을 위한 수학을 번역해 올리려 합니다.
• 번역은 LLM(현재는 GPT-4)를 통해 번역하고 있습니다.
• 대략의 pipeline은 mathpix를 통해 ocr후 gpt-4로 대략 1000토큰 단위로 나누어 번역하고 있습니다. 논문->ocr을 통한 markdown으로 변경 -> markdown로 작성된 논문을 gpt-4 api로 번역 및 markdown으로 작성
• 현재까지 완성된 파이프라인은 https://github.com/aeolian83/paper_translator 입니다
• 원문 링크는 다음과 같습니다.
  • https://homepages.warwick.ac.uk/staff/Martin.Lotz/files/learning/lectnotes-all.pdf

서론

"어떤 컴퓨터도 자신이 무엇을 하고 있는지 인식한 적이 없다; 하지만 대부분의 경우, 우리도 그렇다."

— 마빈 민스키(Marvin Minsky), 1927-2016

학습은 정보와 경험을 지식과 이해로 변환하는 과정입니다. 지식과 이해는 특정 작업을 독립적으로 수행할 수 있는 능력으로 측정됩니다. 따라서 기계 학습(Machine Learning)은 학습 과정의 결과에 기반하여 컴퓨터 시스템이 특정 작업을 독립적으로 수행할 수 있도록 하는 알고리즘과 모델을 연구하는 것입니다. 학습 작업은 손글씨 숫자 인식과 같은 간단한 분류 문제부터 의료 진단이나 자동차 운전과 같은 더 복잡한 작업에 이르기까지 다양할 수 있습니다.

기계 학습은 인공 지능(Artificial Intelligence)의 더 넓은 분야의 일부이지만, 기계가 제공된 엄격한 규칙 세트를 따르는 더 전통적인 문제 해결 방식과는 구별됩니다. 이러한 이유로, 기계 학습은 인간에게는 간단하지만 정확한 규칙을 찾기 어려운 패턴 인식(pattern recognition)과 같은 작업이나, 간단한 규칙을 허용하지만 문제의 복잡성으로 인해 규칙 기반 접근이 계산상 불가능한 작업에 가장 유용합니다. 후자의 대표적인 예는 보드 게임 바둑(Go)에서 인간을 능가하는 성능을 달성한 딥마인드(DeepMind)의 알파고(AlphaGo) ${ }^{1}$와 같은 강화 학습(reinforcement learning) 기반 컴퓨터 프로그램의 최근 성공입니다. 게임의 규칙은 간단하지만, 가능한 위치의 수로 인해 발생하는 어마어마한 복잡성 때문에 최고의 인간 플레이어를 이기는 것은 10년 전만 해도 불가능해 보였습니다.

학습을 위한 일반적인 프레임워크

기계 학습은 근사 이론(approximation theory), 확률 이론(probability theory), 통계(statistics), 그리고 최적화 이론(optimization theory)의 교차점에 있습니다. 우리는 몇 가지 기본 예제를 통해 이 분야들의 상호 작용을 설명합니다.

가장 기본적인 형태에서, 기계 학습의 목표는 함수를 찾아내는(학습하는) 것입니다.

여기서 $\mathcal{X}$는 입력 또는 특징(features)의 공간이고, $\mathcal{Y}$는 출력 또는 반응(responses)으로 구성됩니다. 입력 공간 $\mathcal{X}$는 보통 메트릭 공간(metric space) (예: $\mathbb{R}^{d}$)으로 모델링되며, 입력은 이미지, 텍스트, 이메일, 유전자 서열, 네트워크, 금융 시계열 또는 인구 통계 데이터를 나타낼 수 있습니다. 출력은 온도나 몸 안의 특정 물질의 양과 같은 양적인 값이거나 $\{\mathrm{YES}, \mathrm{NO}\}$ 또는 $\{0,1,2,3,4,5,6,7,8,9\}$와 같은 질적 또는 범주적인 값으로 구성될 수 있습니다. 첫 번째 유형의 문제는 보통 회귀(regression)라고 하며, 후자는 분류(classification)라고 합니다. 함수 $h$는 때때로 가설(hypothesis), 예측기(predictor), 또는 분류기(classifier)라고 불립니다. 오직 두 가지 값(일반적으로 0과 1, 또는 -1과 1)만을 취하는 분류기 $h$는 이진 분류기(binary classifier)라고 불립니다. 기계 학습 시나리오에서 함수 $h$는 가설 공간(hypothesis space)이라고 불리는 미리 정해진 함수들의 집합 $\mathcal{H}$에서 선택됩니다.

기계 학습 문제는 지도 학습(supervised learning)과 비지도 학습(unsupervised learning) 문제로 나눌 수 있습니다. 지도 학습에서는 입력-출력 데이터 쌍의 컬렉션을 사용할 수 있습니다.

그리고 목표는 이 데이터로부터 함수 $h: \mathcal{X} \rightarrow \mathcal{Y}$를 학습하는 것입니다. 쌍의 컬렉션 $\left\{\left(\boldsymbol{x}^{i}, \boldsymbol{y}^{i}\right)\right\}_{i=1}^{n}$은 훈련 세트(training set)라고 불립니다. 비지도 학습에서는 훈련 세트에 접근할 수 없습니다. 비지도 학습 작업의 전형적인 예는 클러스터링(clustering)으로, 주어진 데이터 세트를 유사성에 기반하여 그룹으로 나누는 작업입니다. 이 강의는 주로 지도 학습에 대해 다룰 것입니다.

예제 1.1 (숫자 인식). 픽셀 행렬의 데이터셋이 주어지고, 각각의 회색조 이미지를 나타내며, 각 이미지가 나타내는 숫자를 알려주는 레이블이 연관되어 있을 때, 이 데이터를 사용하여 컴퓨터 프로그램을 훈련시켜 새로운 숫자를 인식하도록 하는 것이 과제입니다(그림 1.1 참조). 이러한 분류 작업은 강력한 비선형 함수의 클래스인 심층 신경망(deep neural networks)을 사용하여 종종 수행됩니다.

그림 1.1: MNIST(수정된 국립표준기술연구소, http://yann.lecun.com/exdb/mnist/) 데이터셋은 손으로 쓴 숫자들의 대규모 이미지 모음이며, 기계 학습(machine learning)에서 자주 사용되는 벤치마크입니다.

예제 1.2. (클러스터링) 클러스터링 응용에서는 데이터 $\left\{\boldsymbol{x}^{i}\right\}_{i=1}^{n}$를 관찰하고, 유사성을 기반으로 데이터를 여러 개의 구별되는 그룹으로 나누는 것이 목표입니다. 여기서 유사성은 거리 함수를 사용하여 측정됩니다. 그림 1.2는 인공 클러스터링 문제와 가능한 해결책을 보여줍니다.

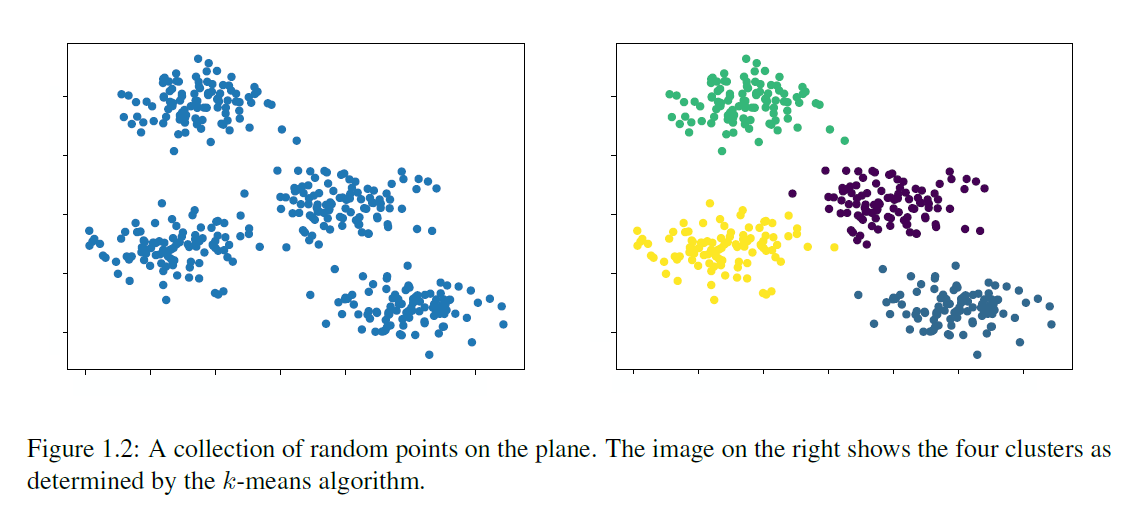
그림 1.2: 평면 위의 무작위 점들의 모음. 오른쪽 이미지는 $k$-평균(k-means) 알고리즘에 의해 결정된 네 개의 클러스터를 보여줍니다.

사용되는 거리 개념은 응용 프로그램에 따라 다릅니다. 예를 들어, 이진 시퀀스나 DNA 시퀀스의 경우 두 시퀀스가 다른 위치를 단순히 계산하는 해밍 거리(Hamming metric)를 사용할 수 있습니다. 클러스터링은 유전학, 생물학, 의학 등에서 광범위하게 사용됩니다. 예를 들어, 클러스터링은 공통 생물학적 경로의 일부인 단백질을 인코딩하는 유전자 그룹(기능을 가진 DNA의 부분)을 식별하는 데 사용될 수 있습니다. 클러스터링의 다른 용도로는 시장 세분화와 네트워크 내 커뮤니티 탐지가 있습니다.

근사 이론(Approximation Theory)

관찰된 훈련 데이터가 알려지지 않은 함수 $f: \mathcal{X} \rightarrow \mathcal{Y}$에서 온다는 단순화된 가정을 종종 합니다. 목표는 유한한 샘플 집합 $\left\{\boldsymbol{x}^{i}, \boldsymbol{y}^{i}\right\}_{i=1}^{n}$만을 알고 있는 상태에서 가설 클래스 $\mathcal{H}$의 함수 $h$로 함수 $f$를 근사하는 것입니다. 여기서 우리는 $\boldsymbol{y}^{i} \approx f\left(\boldsymbol{x}^{i}\right)$라고 가정합니다. 적절한 함수 클래스는 해당 응용 프로그램, 계산 및 통계적 고려사항에 따라 다릅니다. 많은 경우 선형 함수가 잘 작동하지만, 다른 상황에서는 다항식이나 신경망(neural networks)과 같은 더 복잡한 함수가 더 적합합니다.

예제 1.3. (선형 회귀) 선형 회귀(Linear regression)는 다음과 같은 형태의 관계를 찾는 문제입니다.

여기서 $X_{1}, \ldots, X_{p}$는 시스템의 특정 특성을 설명하는 공변량(covariates)이고 $Y$는 반응(response)입니다. 입력-출력 쌍 $\left(\boldsymbol{x}^{i}, y^{i}\right)$을 행렬 $\boldsymbol{X}$와 벡터 $\boldsymbol{y}$에 배열한 후, 최소 제곱 최적화 문제를 풀어 올바른 $\boldsymbol{\beta}=\left(\beta_{0}, \beta_{1}, \ldots, \beta_{p}\right)^{\top}$를 추정할 수 있습니다.

그림 1.3은 선형 회귀의 예를 보여줍니다.

예제 1.4. (텍스트 분류) 텍스트 분류(Text classification)에서의 작업은 주어진 텍스트가 주어진 카테고리 집합 중 어디에 속하는지 결정하는 것입니다. 훈련 데이터는 단어의 가방(bag of words)으로 구성됩니다: 이것은 컬럼이 단어를 나타내고 행이 기사를 나타내는 큰 희소 행렬로, $(i, j)$-번째 항목에는 단어 $j$가 텍스트 $i$에 포함된 횟수가 들어 있습니다.

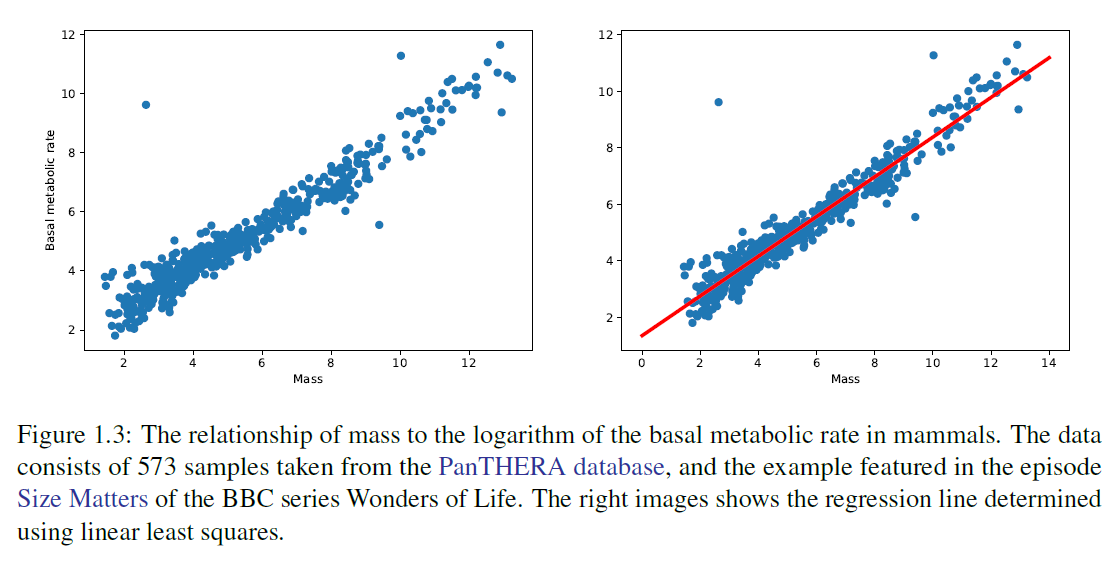
그림 1.3: 포유류의 질량과 기초 대사율의 로그 값과의 관계. 데이터는 PanTHERA 데이터베이스에서 가져온 573개의 샘플로 구성되어 있으며, BBC 시리즈 'Wonders of Life'의 에피소드 'Size Matters'에서 소개된 예시입니다. 오른쪽 이미지는 선형 최소 제곱법을 사용하여 결정된 회귀선을 보여줍니다.

	목표(Goal)	수프(Soup)
기사 1(Article 1)	5	0
기사 2(Article 2)	1	7

예를 들어, 위의 세트에서 첫 번째 기사를 "스포츠(Sports)"로, 두 번째 기사를 "음식(Food)"으로 분류할 것입니다. 이러한 훈련 데이터셋의 한 예는 Reuters Corpus Volume I (RCV1) ${ }^{2}$로, 800,000개가 넘는 분류된 뉴스 기사 아카이브입니다. 이러한 문제에 대한 전형적인 이진 분류기(binary classifier)는 다음과 같은 형태의 선형 분류기(linear classifier)일 것입니다.

여기서 $\boldsymbol{w} \in \mathbb{R}^{d}$이고 $b \in \mathbb{R}$입니다. 데이터셋의 한 행으로 표현된 텍스트 $\boldsymbol{x}$가 주어지면, $h(\boldsymbol{x})>0$이면 $\{+1\}$ 클래스로, $h(\boldsymbol{x})<0$이면 $\{-1\}$ 클래스로 분류됩니다.

예시 1.5. (딥 뉴럴 네트워크(Deep Neural Networks)) 뉴럴 네트워크는 다음과 같은 형태의 함수입니다.

여기서 각 $f_{k}$는 활성화 함수(activation function) $\sigma$와 선형 맵 $\mathbb{R}^{d_{k-1}} \rightarrow$ $\mathbb{R}^{d_{k}}, \boldsymbol{x} \mapsto \boldsymbol{W}^{k} \boldsymbol{x}+\boldsymbol{b}^{k}$의 요소별(element-wise) 합성입니다. 활성화 함수로는 시그모이드(sigmoid) $\sigma(x)=1 /\left(1+\mathrm{e}^{-x}\right)$가 있으며, 이는 $(0,1)$ 사이의 값을 가지며, 양수 또는 음수인 좌표를 "선택"하는 것으로 해석될 수 있습니다(그림 1.4 참조). 각 층의 행렬 $\boldsymbol{W}^{k}$의 계수 $w_{i j}^{k}$는 가중치(weights)이며, $\boldsymbol{b}^{k}$의 항목은 편향(bias terms)이라고 불립니다. 가중치와 편향은 관찰된 입력-출력 쌍에 맞게 조정되어야 합니다. 뉴럴 네트워크는 보통 그래프로 표현되며, 그림 1.5를 참조하세요. 뉴럴 네트워크는 패턴 인식에서 매우 성공적이었으며, 자연어 처리부터 기계 번역, 의료 진단에 이르기까지 다양한 응용 분야에서 널리 사용됩니다.

근사 이론(approximation theory)에서 가장 초기의 이론적 결과 중 하나는 바이어슈트라스(Weierstrass)의 정리로, 우리가 임의의 정밀도로 다항식으로 연속 함수를 근사할 수 있음을 보여줍니다.

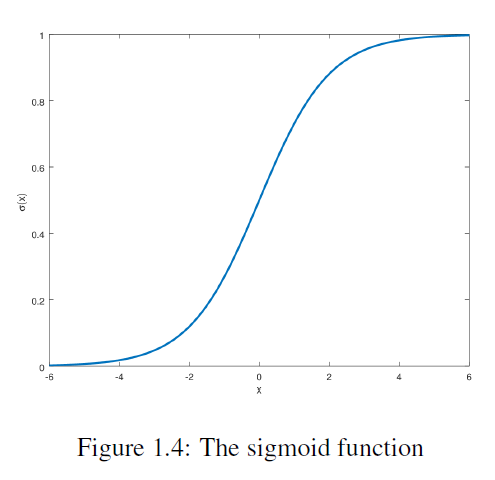
그림 1.4: 시그모이드 함수

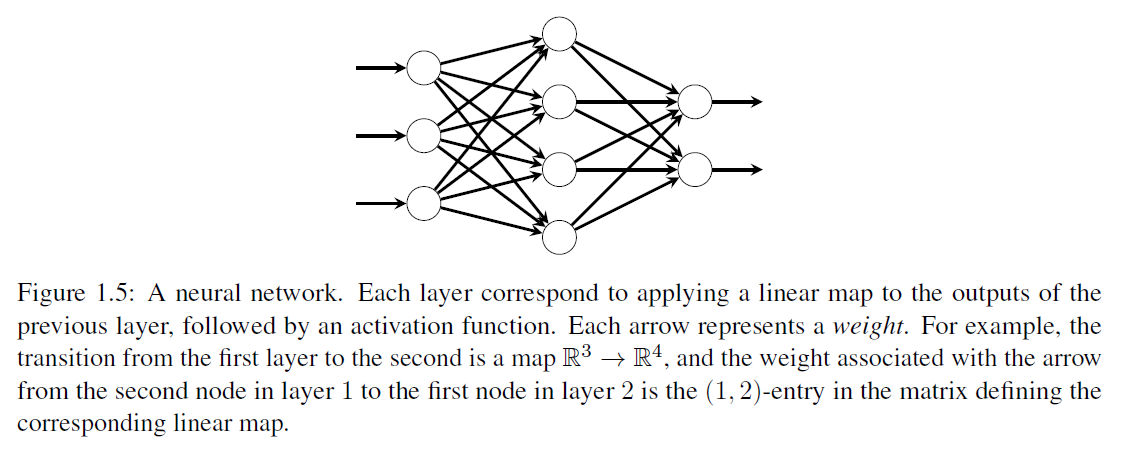
그림 1.5: 뉴럴 네트워크. 각 층은 이전 층의 출력에 선형 맵을 적용한 다음 활성화 함수를 적용하는 것에 해당합니다. 각 화살표는 가중치를 나타냅니다. 예를 들어, 첫 번째 층에서 두 번째 층으로의 전환은 $\mathbb{R}^{3} \rightarrow \mathbb{R}^{4}$ 맵이며, 1층의 두 번째 노드에서 2층의 첫 번째 노드로의 화살표와 관련된 가중치는 해당 선형 맵을 정의하는 행렬의 $(1,2)$-항목입니다.

정리 1.6 (바이어슈트라스(Weierstrass)). $f$가 $[a, b]$에서 연속 함수일 때, 모든 $\epsilon>0$에 대해 다음을 만족하는 다항식 $p(x)$가 존재합니다.

이 정리는 우리가 다항식의 계수라는 유한한 수의 매개변수만을 사용하여 콤팩트 구간(compact interval) 상의 모든 연속 함수를 근사할 수 있다는 것을 보여주기 때문에 주목할 만합니다. 이 정리의 문제점은 다항식의 크기에 대한 상한을 제공하지 않는다는 것으로, 이는 상당히 클 수 있습니다. 또한 실제로 이러한 근사를 계산하는 절차를 제공하지 않으며, 효율적으로 찾는 방법은 더더욱 없습니다. 우리는 신경망(neural networks)이 같은 근사 속성을 가지고 있음을 볼 것입니다. 즉, 구간(interval) 상의 모든 연속 함수는 신경망에 의해 임의의 정확도로 근사될 수 있습니다. 더 단순한 클래스를 통해 함수 클래스를 근사하는 것에 대한 많은 변형이 있으며, 우리는 이러한 근사를 효율적으로 계산할 수 있는 경우에 관심을 가질 것입니다. 좋은 근사 함수를 찾는 한 가지 방법은 최적화 방법(optimization methods)을 사용하는 것입니다.

최적화(Optimization)

최적의 적합성(best fit) 개념은 손실 함수(loss function)를 사용하여 형식화됩니다. 손실 함수 $L: \mathcal{Y} \times \mathcal{Y} \rightarrow \mathbb{R}_{+}$는 주어진 입력 $\boldsymbol{x} \in \mathcal{X}$에 대한 예측과 요소 $\boldsymbol{y} \in \mathcal{Y}$ 사이의 불일치를 측정합니다. 함수 $h: \mathcal{X} \rightarrow \mathcal{Y}$의 경험적 위험(empirical risk)은 훈련 데이터(training data)에 대한 평균 손실 $L\left(h\left(\boldsymbol{x}^{i}\right), \boldsymbol{y}^{i}\right)$입니다,

그런 다음 후보 함수 집합 $\mathcal{H}$ 중에서 훈련 데이터에 함수를 적용할 때 손실을 최소화하는 함수 $h$를 찾고자 합니다:

문제 (1.1)은 최적화 문제입니다. 함수 집합에 대한 최소화는 추상적으로 보일 수 있지만, $\mathcal{H}$의 함수들은 일반적으로 몇 개의 매개변수로 표현됩니다. 예를 들어, 클래스 $\mathcal{H}$가 예제 1.3에서처럼 형태가 $\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{p} x_{p}$인 선형 함수들로 구성되어 있다면, 최적화 문제 (1.1)는 $\mathbb{R}^{p+1}$ 상에서 함수를 최소화하는 것과 같습니다. 신경망(neural networks)의 경우, 예제 1.5에서처럼 가중치 $w_{i j}^{k}$와 편향 항 $b_{i}^{k}$에 대해 최적화합니다.

손실 함수의 형태는 문제에 따라 다르며, 보통 통계적 고려에서 유도됩니다. 회귀 문제(regression problems)에 대한 제곱 오차(square error)와 함수 $h: \mathbb{R}^{d} \rightarrow \mathbb{R}$에 적용될 때 형태가

인 지표 손실 함수(indicator loss function)가 흔한 후보입니다. 이 함수는 일반적인 형태로

를 가집니다.

이 함수는 연속적이지 않기 때문에, 실제로는 연속적인 근사치를 자주 접하게 됩니다. 이진 분류기(binary classifier)는 종종 입력이 클래스에 속할 확률을 제공하는 함수 $h: \mathcal{X} \rightarrow[0,1]$에 의해 구현됩니다. 만약 $h(\boldsymbol{x})>1 / 2$이면, $\boldsymbol{x}$는 클래스 1에 할당되고, $h(\boldsymbol{x}) \leq 1 / 2$이면, $\boldsymbol{x}$는 클래스 0에 할당됩니다. 이 설정에 대한 일반적인 손실 함수는 로그 손실 함수(log-loss function) 또는 교차 엔트로피(cross-entropy)입니다,

이 함수는 $h(\boldsymbol{x})$가 예측하는 클래스가 $y$와 일치하지 않을 경우 큰 값을 가지도록 설계되었으며, 최대 우도 추정(maximum-likelihood estimation)의 맥락에서 해석될 수 있습니다.

함수의 최소화자(minimizer)를 찾거나 근사하는 것은 수치 최적화(numerical optimization)의 영역에 속합니다. 선형 회귀(linear regression)의 경우 관련 최적화 문제(최소 제곱법(least-squares minimization))를 닫힌 형태(closed form)로 풀 수 있지만, 신경망(neural networks)과 같은 더 복잡한 문제의 경우 경사 하강법(gradient descent)과 같은 최적화 알고리즘을 사용합니다: 초기 추측값에서 시작하여 가장 가파른 하강 방향, 즉 함수의 음의 기울기(negative gradient)를 따라 함수를 최소화하기 위해 단계를 진행합니다. 신경망과 같은 합성 함수(composite functions)의 경우, 기울기를 계산하기 위해 연쇄 법칙(chain rule)이 필요하며, 이는 신경망을 훈련하기 위한 유명한 역전파 알고리즘(backpropagation algorithm)으로 이어집니다. 이에 대해서는 자세히 논의될 것입니다.

최적화 모델과 알고리즘에는 많은 도전과제가 있습니다. 최소화해야 할 함수에는 많은 국소 최소점(local minima)이나 안장점(saddle points)이 있을 수 있으며, 최소화자를 찾는 알고리즘은 전역 최소점(global minimizer) 대신 이 중 하나를 찾을 수 있습니다. 최소화해야 할 함수가 미분 불가능할 수도 있으며, 비매끄러운 최적화(non-smooth optimization) 분야의 방법론이 적용됩니다. 그러나 기계 학습(machine learning)의 맥락에서 최적화 알고리즘에 대한 가장 큰 도전은 목적 함수(objective function)의 특정 형태에 있습니다: 각 데이터 포인트마다 하나씩, 많은 항의 합으로 주어집니다. 이러한 함수를 평가하고 그 기울기를 계산하는 것은 시간과 메모리를 많이 소모할 수 있습니다. 확률적 경사 하강법(stochastic gradient descent)을 포함하는 오래된 알고리즘 클래스는 각 단계에서 전체 함수의 기울기를 계산하는 대신, 항의 작은 무작위 부분집합만의 기울기를 계산함으로써 이 문제를 우회합니다. 이 알고리즘들은 모든 정보를 매 단계에서 사용하지 않음에도 불구하고 놀랍도록 잘 작동합니다.

통계(Statistics)

이진 분류 작업(binary classification task)을 가정해 보겠습니다. 여기서 $\mathcal{Y}=\{0,1\}$입니다. 우리는 데이터로부터 다음과 같은 함수를 학습할 수 있습니다:

이것은 기억에 의한 학습(learning by memorization)이라고 불립니다. 왜냐하면 함수는 단순히 본 예제 $\boldsymbol{x}^{i}$에 대한 값 $y^{i}$를 기억합니다. 이 문제에 대한 단위 손실 함수(unit loss function)에 대한 경험적 위험(empirical risk)은

입니다. 그럼에도 불구하고, 이것은 좋은 분류기(classifier)가 아닙니다: 훈련 세트(training set) 외부에서는 매우 잘 수행되지 않을 것입니다. 이것은 과적합(overfitting)의 한 예입니다: 함수가 본 데이터에 너무 밀접하게 적응되어 보이지 않는 데이터에 일반화하지 못합니다. 일반화(generalization) 문제는 보이지 않는 데이터에서 잘 작동하는 분류기를 찾는 문제입니다.

일반화의 개념을 더 명확하게 하기 위해, 훈련 데이터 포인트 $\left(\boldsymbol{x}^{i}, \boldsymbol{y}^{i}\right)$가 $\mathcal{X} \times \mathcal{Y}$의 곱집합에서 샘플링된 (알려지지 않은) 확률 분포로부터 추출된 무작위 변수(random variables) $(X, Y)$의 실현(realizations)이라고 가정합니다. 변수 $X$와 $Y$는 일반적으로 독립적이지 않습니다(그렇지 않으면 배울 것이 없을 것이기 때문에), 하지만 $Y=f(X)+\epsilon$ 형태의 관계로 연결되어 있습니다. 여기서 $\epsilon$은 기대값이 $\mathbb{E}[\epsilon]=\mathbf{0}$인 무작위 교란(random perturbation)입니다. 무작위 잡음 $\epsilon$의 존재는 불확실성이나 누락된 정보를 나타내는 것으로 해석될 수 있습니다. 예를 들어, 유전적 마커를 기반으로 특정 질병을 예측하려고 할 때, 유전 데이터는 항상 정확한 예측을 할 수 있을 만큼 충분한 정보를 담고 있지 않을 수 있습니다. 함수 $f$는 회귀 함수(regression function)라고 불립니다. 이것은 주어진 $X$ 값에 대한 $Y$의 조건부 기대값(conditional expectation)입니다,

분류기 $h \in \mathcal{H}$와 손실 함수 $L$이 주어졌을 때, 일반화 위험(generalization risk)은 기대값으로 정의됩니다.

만약 $L(h(\boldsymbol{x}), \boldsymbol{y})=\mathbf{1}\{h(\boldsymbol{x}) \neq \boldsymbol{y}\}$가 단위 손실(unit loss)이라면, 이것은 단순히 $\mathbb{P}\{h(X) \neq Y\}$, 즉 무작위로 선택된 입력-출력 쌍을 잘못 분류할 확률입니다. 학습 데이터는 $n$ 쌍의 무작위 변수

로부터의 샘플링으로 모델링될 수 있으며, 이들은 $(X, Y)$의 동일하게 분포되고 독립적인 복사본입니다. 분류기 $h$가 주어지면, 경험적 위험(empirical risk)은 무작위 변수가 됩니다.

이 무작위 변수의 기대값은

입니다. 여기서 우리는 기대값의 선형성과 $\left(X_{i}, Y_{i}\right)$가 독립적이고 동일하게 분포되어 있다는 사실(i.i.d)을 사용했습니다. 따라서 경험적 위험 $\hat{R}(h)$은 일반화 위험 $R(h)$의 편향되지 않은 추정치(unbiased estimator)입니다.

예시 1.7. 손실 함수는 종종 경험적 위험 최소화 문제가 최대 우도 추정(maximum likelihood estimation) 문제가 되도록 선택됩니다. 예를 들어, $Y$가 $\{0,1\}$의 값을 가지며 $\mathbb{P}\{Y=1 \mid X=\boldsymbol{x}\}=f(\boldsymbol{x})$의 확률로 주어진 경우를 생각해보세요. $X=\boldsymbol{x}$에 조건을 걸었을 때, $Y$는 매개변수 $p=f(\boldsymbol{x})$를 가진 베르누이(Bernoulli) 무작위 변수이며, 로그 손실 함수(log-loss function) (1.2)는 매개변수 $p$를 추정하는 문제에 대한 음의 로그 우도 함수(negative log-likelihood function)입니다.

좋은 가설 $h$를 찾을 때, 우리가 사용할 수 있는 것은 학습 데이터로부터 구성된 경험적 위험 함수뿐입니다. 가설 클래스 $\mathcal{H}$에서 경험적 위험 최소화자 $\hat{h}$의 품질은 추정 오류(estimation error)로 측정될 수 있는데, 이는 $\hat{h}$의 일반화 위험과 $\mathcal{H}$에서 가능한 가장 작은 일반화 위험을 비교하고, 근사 오류(approximation error)는 $\mathcal{H}$ 내에서 일반화 위험이 얼마나 작아질 수 있는지를 측정합니다. 일반적으로 이 두 오류 사이에는 트레이드오프(trade-off)가 있습니다: 만약 함수의 클래스 $\mathcal{H}$가 크다면, 작은 일반화 위험을 가진 함수를 포함할 가능성이 높고 따라서 근사 오류가 작을 것입니다. 하지만 경험적 위험 최소화자 $\hat{h}$는 데이터에 "과적합(overfit)"할 가능성이 높고 잘 일반화하지 못할 것입니다. 반면에, $\mathcal{H}$가 작다면(극단적인 경우, 단 하나의 함수만으로 구성된 경우), 경험적 위험 최소화자는 $\mathcal{H}$ 내에서 가능한 최선의 가설에 가까울 것이지만, 근사 오류는 클 것입니다. 그림 1.6은 노이즈가 있는 함수로부터의 데이터가 다른 차수의 다항식으로 근사되는 예를 보여줍니다.

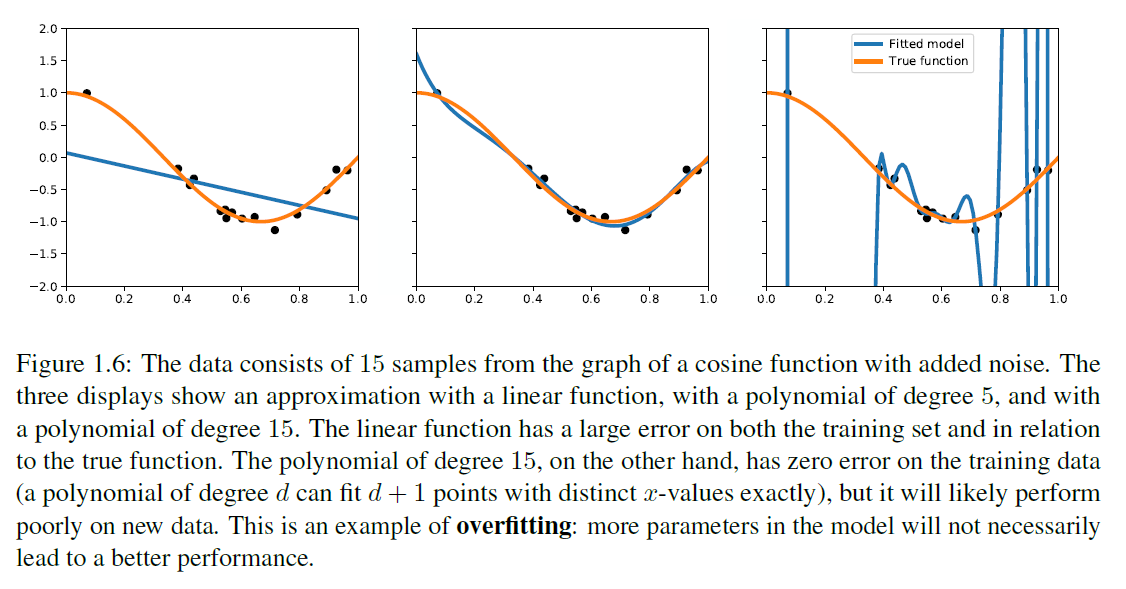
그림 1.6: 데이터는 코사인 함수(cosine function)의 그래프에서 추출한 15개의 샘플로, 노이즈가 추가되었습니다. 세 가지 디스플레이는 선형 함수(linear function), 5차 다항식(polynomial of degree 5), 그리고 15차 다항식(polynomial of degree 15)으로 근사화한 것을 보여줍니다. 선형 함수는 훈련 데이터(training set)와 실제 함수(true function)에 대해 큰 오차를 가지고 있습니다. 반면에, 15차 다항식은 훈련 데이터에 대해 오차가 없습니다(차수 $d$의 다항식은 서로 다른 $x$-값을 가진 $d+1$개의 점을 정확히 맞출 수 있습니다), 하지만 새로운 데이터에 대해서는 아마도 성능이 좋지 않을 것입니다. 이것은 과적합(overfitting)의 한 예입니다: 모델에 더 많은 매개변수가 있다고 해서 반드시 더 나은 성능을 보장하지는 않습니다.

통계 학습 이론(Statistical Learning Theory) 분야는 일반화 위험성(generalization risk), 경험적 위험성(empirical risk), 가설 클래스(hypothesis class) $\mathcal{H}$의 용량(capacity), 그리고 샘플의 수 $n$ 사이의 관계를 이해하려고 합니다. 특히, 가설 클래스의 용량과 같은 개념은 VC 차원(VC dimension), 라데마허 복잡도(Rademacher complexity), 커버링 수(covering numbers)와 같은 개념을 통해 정확한 의미를 부여받습니다.

노트

현대 기계 학습(machine learning)을 뒷받침하는 근사 이론(approximation theory), 최적화(optimization), 통계(statistics)에서 온 아이디어들은 오래되었습니다. 선형 회귀(linear regression)는 르장드르(Legendre)와 가우스(Gauss)에게 알려져 있었습니다. 바이어슈트라스 근사 정리(Weierstrass Approximation Theorem)는 바이어슈트라스(Weierstrass)에 의해 [31]에서 발표되었으며, 근사 이론에 대한 더 많은 역사는 [28, Chapter 6]에서 볼 수 있습니다. 신경망(neural networks)은 1943년 맥컬록(McCulloch)과 피츠(Pitts)의 개척적인 작업 [16]으로 거슬러 올라가며, 이어서 로젠블라트(Rosenblatt)의 퍼셉트론(Perceptron) [22]이 등장했습니다. "기계 학습(Machine Learning)"이라는 용어는 아서 사무엘(Arthur Samuel)에 의해 1959년 [24]에 처음 사용되었으며, 당시에는 "사이버네틱스(Cybernetics)"가 여전히 널리 사용되고 있었습니다. 경사 하강법(Gradient descent)은 코시(Cauchy)에게 알려져 있었고, 오늘날 딥 러닝(deep learning)에 있어 가장 중요한 알고리즘인 확률적 경사 하강법(Stochastic Gradient Descent)은 1951년 로빈스(Robbins)와 먼로(Monro)에 의해 소개되었습니다 [21]. 통계 학습 이론 분야는 1960년대 바프닉(Vapnik)과 체르보넨키스(Chervonenkis)의 개척적인 작업을 통해 생겨났으며, 개요는 [29]에서 볼 수 있습니다. 수학적 학습 이론에 대한 설명은 [5]에서 볼 수 있습니다.

1990년대에 기계 학습 연구는 폭발적으로 증가했으며, 놀라운 새로운 결과와 응용이 숨가쁘게 등장했습니다. 그러나 학습 이론과 고차원 확률론에서의 일부 이론적 발전을 제외하고, 이러한 돌파구들은 50년 전에 사용할 수 없었던 수학에 거의 의존하지 않았습니다. 그렇다면 사이버네틱스의 초기 시절 이후 무엇이 변했을까요? 갑작스러운 인기 급증의 주된 이유는 방대한 양의 데이터와 마찬가지로 중요한, 데이터를 처리할 수 있는 계산 자원의 가용성입니다. 새로운 응용은 차례로 새로운 수학적 문제를 제기하고, 다양한 분야 간의 새로운 연결을 만들어냈습니다.

[^0]: ${ }^{1}$ https://deepmind.com/research/case-studies/alphago-the-story-so-far