목표

• 그래프를 이해한다.
• 그래프에서 DFS를 이해한다.
• 그래프에서 BFS를 이해한다.
• 자바 코드로 구현을 통해 이해한다.

Graph

그래프를 왜 쓸까?

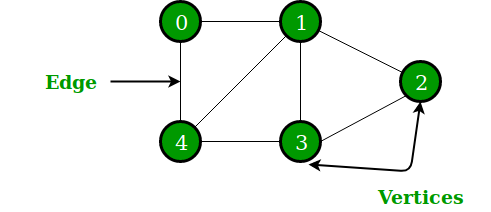
• 현실의 객체 간 관계를 표현할 수 있다.
  현실에서 어떤 데이터는 객체와 객체 간의 관계로 표현되고 있다.
  도로와 도로, 차와 차, 네트워크 포인트와 포인트 등
  이러한 객체 관계를 가장 잘 표현 가능하다.

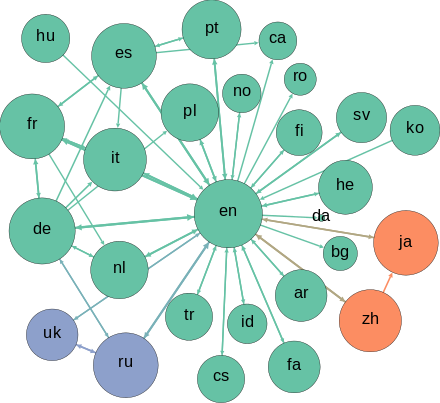
• 객체와 객체 간 관계에 따른 관계식을 가장 쉽게 구할 수 있다.
  최단경로를 구한다던가, 가장 비효율적인 길을 제외한다던가, 회로망을 만드는 등에 사용가능하다.

그래프의 구성

• Vertex
  각 에지와 연결 된 노드
• Edge
  각 노드 간 연결된 선
  ===> Vertex = Node, Edge = Link
• Adjacent Vertex
  인접 정점
• Degree
  정점 간 길이

그래프의 종류

무방향성 그래프(Undirected Graph)

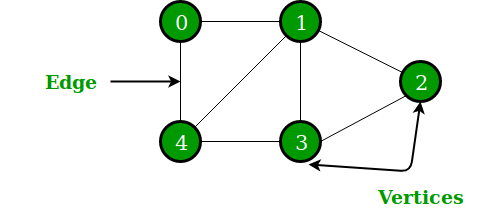
• 그래프 Vertex(정점) 간 방향성이 존재하지 않음
• 그래프 (0, 1)은 (1,0)과 동일하다

방향성 그래프(Directed Graph)

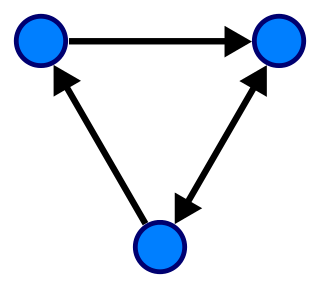
• 그래프 Vertex 간 방향성이 존재
• 그래프 A -> B가 있어도 B -> A는 존재하지 않을 수 있음

가중치 그래프(Weighted Graph)

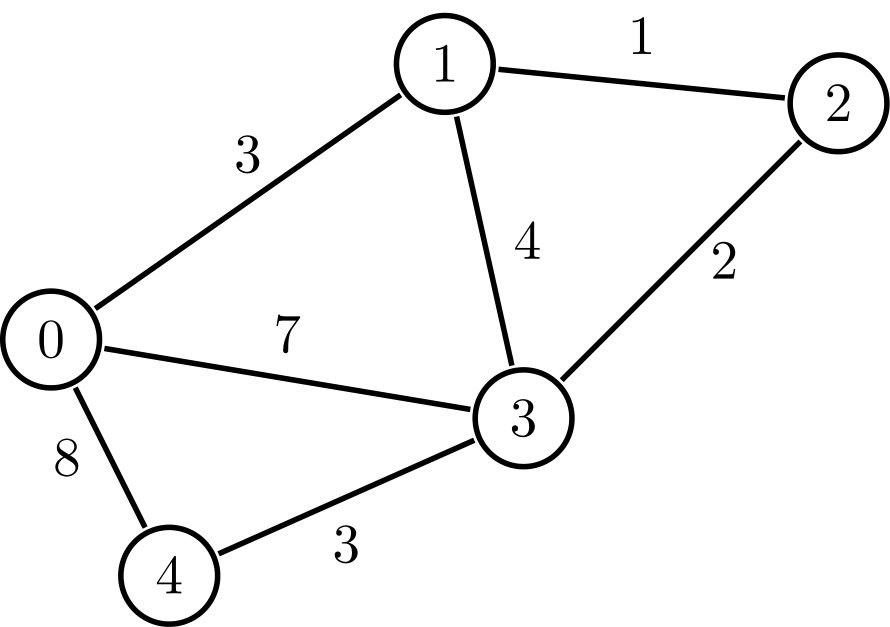
• Edge에 가중치가 존재
• 가중치는 거리, 비용, 용량이 될 수 있음

그래프 경로와 연결성

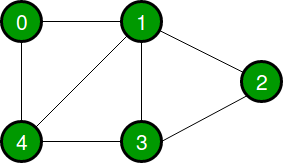
• 인접하는 정점이 있을 때 지나는 경로가 있다면 정점 둘은 연결됐다고 한다.
  $graph(0, 1)$
  $graph(1, 3)$ 이 둘은 인접해 있는 정점이고
  $graph(0, 3)$ 은 연결되어 있다고 한다.

그래프의 특징

• 네트워크 관계 모델
• 그래프는 Cycle이 존재할 수도 없을 수도 있음
• 그래프엔 루트, 자식, 부모가 존재하지 않는다

그래프의 구현

• 그래프는 인접 행렬과 인접 리스트를 통해 구현할 수 있다.

가중치 없는 무방향성 그래프

무방향성 그래프 인접 행렬

• $N*N$ 배열에서 그래프를 표현
• vertex 검색은 O(N)
• edge 검색은 한 행만 보면 되니 O(1)
  정확히는 무방향성 그래프의 경우 대칭 행렬을 이루고 있고 대칭 행렬을 이룬다는 건
  한 행에만 접근하며 된다는 뜻이고 한 행에 접근하는 연산 비용은 $O(1)$이다.

무방향성 그래프 인접 리스트

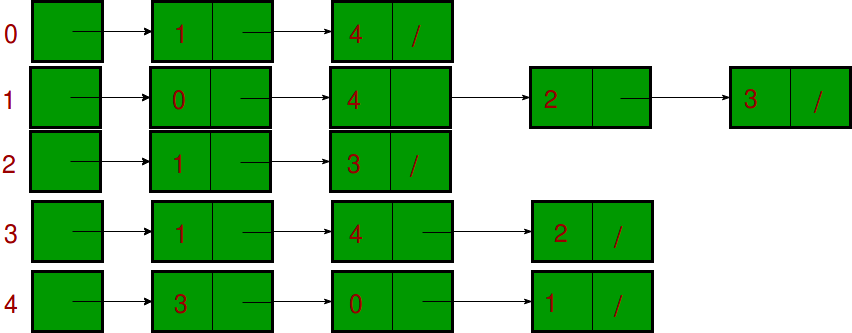
• vertex 배열로부터 링크드 리스트를 통해 표현
• 링크드 리스트의 개수는 degree
• 노드 개수는 $2m$으로 m은 edge의 개수
• 저장 공간은 $n + 2m$ = $O(n+m)$
  최악의 경우 모든 edeg가 중첩 되므로 $O(N^2)$
• vertex에 대한 vertex 검색은 $O(degree(정점))$
  edge 검색은 $O(degree(인접 정점))$

방향성 그래프

인접 행렬

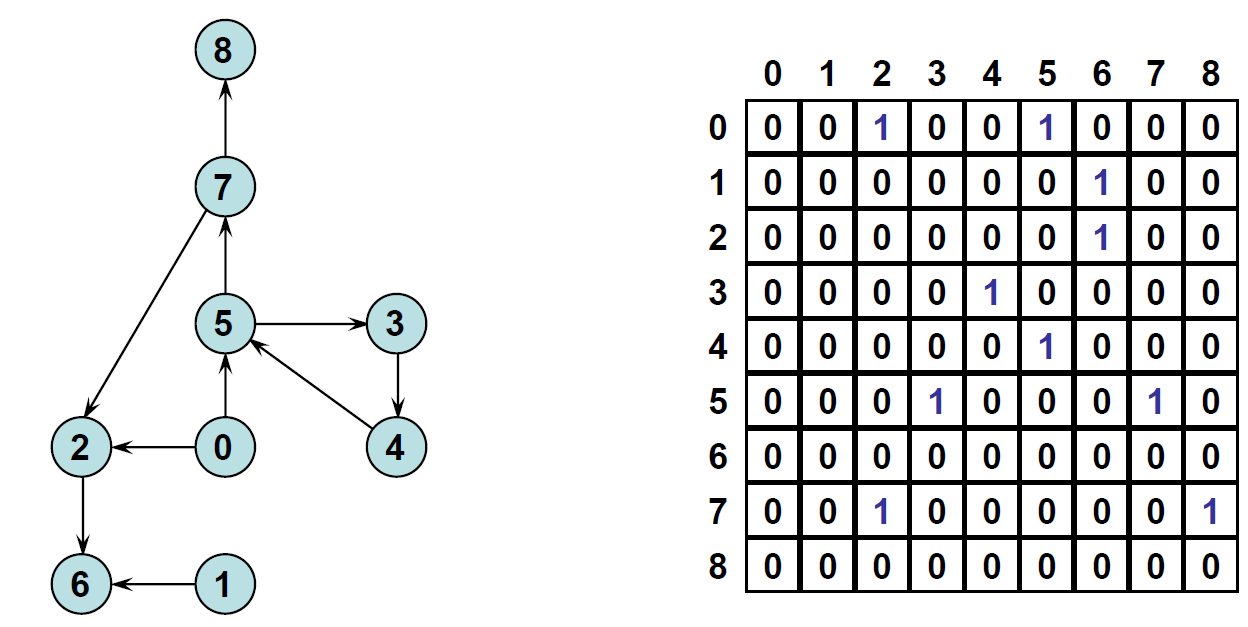
• 방향성은 중복되지 않으므로 대칭 행렬이 아님

인접 리스트

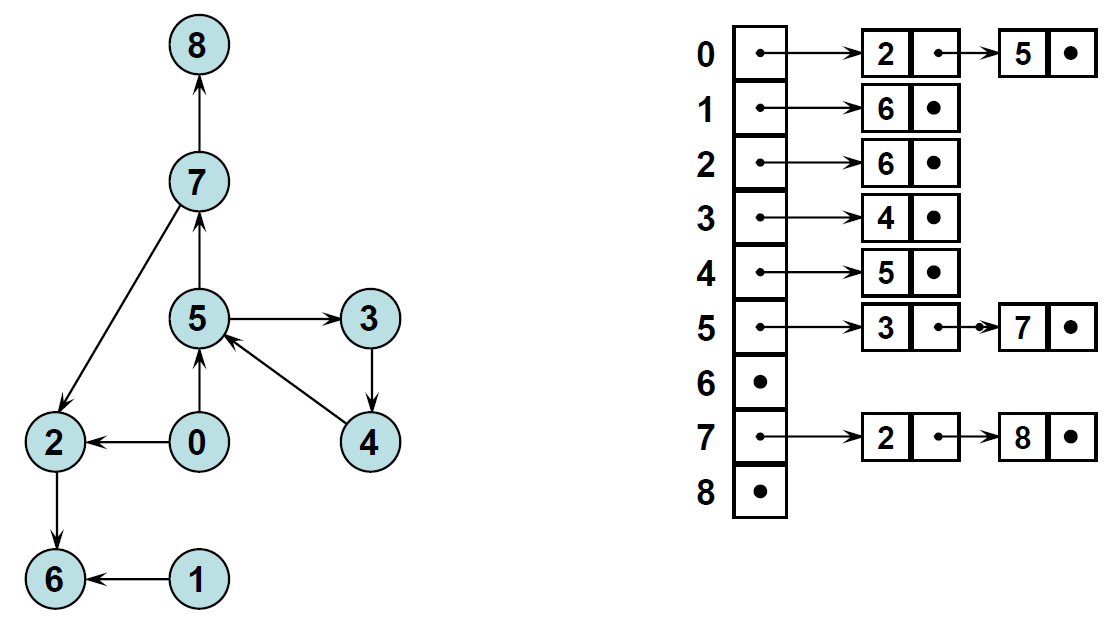
• 방향은 중복되지 않으므로 하나도 존재하지 않는 노드가 있을 수 있음

그래프 구현의 선택

• 따라서 그래프를 구현할 때 인접 행렬을 선택할 것인가, 인접 리스트를 선택할 것인가 선택이 필요함.
• 인접 행렬의 경우
  • $graph(u, v)$일 때 인접 정점 검색 시간 복잡도
    행렬의 행에 접근하면 되므로 $O(1)$
  • $graph(v)$일 때 모든 정점의 검색
    모든 노드를 검색해야 하므로 $O(n)$
  • $graph(u, v)$일 때 공간복잡도는 $O(n^2)$
• 인접 리스트의 경우
  • $graph(u, v)$일 때 인접 정점 검색 시간 복잡도
    정점 $u$에 접근해서 $v$를 검색, 인접 리스트는 degree가 정점의 개수니 $O(d)$
  • $graph(v)$일 때 인접 정점의 검색
    역시 모든 degree를 검색해야하니까 $O(d)$
  • $graph(u, v)$일 때 공간복잡도는 $O(n + m)$
• 따라서 $vertex < edge$인 Dense Graph(밀집) 경우 인접 행렬을 사용
  반대로 $vertex > edge$인 Sparse Graph(드문) 경우 인접 리스트를 쓰는 것이 좋다.

BFS for Graph

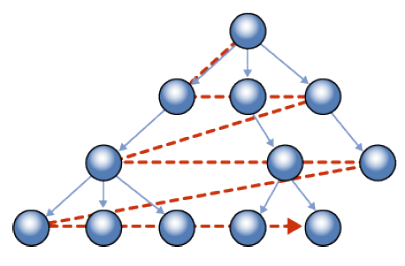
• 시작 정점으로부터 레벨 증가
  트리의 레벨 순회와 똑같음
• Queue를 통해 구현 가능
  각 정점을 Visited Flag를 통해 방문 체크만 해주고 모두 탐색
• 구현
  1. $L0$ 시작
  2. $L1$ 이웃 정점을 모두 탐색
  3. $L1$의 이웃이면서 $L0$이 아닌 정점을 모두 탐색
  4. $Li-1$의 이웃이면서 $Li-2$가 아닌 정점을 모두 탐색
  5. 반복

BFS를 통한 최단 경로

• BFS 트리를 구현
• 각 정점과 에지를 연결한 트리로 구현 됨
• 최단 경로를 찾으면 즉시 종료 가능(다음 레벨로 넘어가지 않으면 됨)

시간 복잡도

• 모든 정점의 flag 초기화 $O(1)$
• 모든 정점을 탐색하므로 $O(n)$
• 결국 하나의 while loop가 전체의 연산과 같다.

DFS for Graph

• 시작 정점으로부터 인접 정점 탐색
  트리의 순회 (In-Order, Pre-Order, Post-Order)와 동일
• 구현
  1. 시작 정점
  2. Visited flag 탐색, 체크되지 않은 정점 방문
  3. 2번 반복
  4. 만약 기준 정점에서 체크되지 않은 정점이 없다면 한칸씩 되돌아오기
  5. 2번 반복
  6. 4번을 통해 시작 정점까지 돌아왔지만 체크되지 않은 정점이 없다면 종료
• 체크되지 않은 정점에 대한 되돌아오기가 존재하므로 Cycle이 형성

DFS를 통한 최단 경로

• 재귀나 스택을 사용해서 체크
• 탐색에 의한 경로가 최단 경로인지 판단 불가, 모든 경로를 체크해야 함
  따라서 최단 경로 탐색에는 BFS를 더 많이 사용

시간 복잡도

• 모든 정점의 flag 초기화 $O(n)$
• 하나의 에지에 flag를 통해 recursion은 한번이기에 에지 개수 $O(m)$
  그리고 정점의 개수 $O(n)$
  결국 시간 복잡도는 모든 정점을 탐색하는 $O(n+m)$

Implementation Graph

인접 리스트 그래프

public class Graph {
    private final List<List<Integer>> graph;

    public Graph(int initSize) {
        this.graph = new ArrayList<>();
        for (int i = 0; i < initSize; i++) {
            graph.add(new ArrayList<>());
        }
    }
public List<Integer> getVertex(int x) {
        return this.graph.get(x);
    }
public static void main(String[] args) {
        Graph graph = new Graph(5);
        graph.singleEdge(0, 1);
        graph.singleEdge(0,4);
        graph.makeEdge(1, 2);
        graph.makeEdge(2, 3);
        graph.makeEdge(1, 4);
        System.out.println(graph.getVertex(1)); // 2, 4
        System.out.println(graph.getVertex(0)); // 1, 4
        System.out.println(graph.getVertex(4)); // 1
    }

전체 코드

• 인접 리스트를 통해 그래프를 구현
  인접 정점을 담을 리스트와 인접 정점들의 기준 정점이 될 배열이 필요했음
  ArrayList<LinkedList<Integer>>로 처음에 만들었는데 검색해보니
  리스트에 대한 탐색이 필요해서 속도를 위해 ArrayList로 담고 있었음

arrGraph graph = new arrGraph(5);
        graph.makeEdge(0, 2);
        graph.makeEdge(1, 4);
        graph.makeEdge(3, 4);
        graph.makeEdge(2, 1);
        System.out.println(Arrays.toString(graph.getVertex(4)));
        graph.printGraph();

전체 코드

[0, 1, 0, 1, 0, 0]
001000
001010
110000
000010
010100
000000

BFS

DFS

참고

권오흠 그래프 알고리즘
영문 위키
ratsgo blog