목표

• 해시와 해시 함수에 대해서 알아본다.
• 해시 테이블에 대해서 알아본다.
• 해시의 충돌과 해시 충돌의 개선에 대해서 알아본다.
• 자바 해시맵에 대해서 알아본다.
• 자바 해시맵을 구현해본다.

해시를 왜 쓸까?

자료구조 공부 시 내가 놓치고 있던 부분은 이걸 왜 쓸까를 먼저 안알아본거였다.
데이터를 쓴다는 건 같은데 이 데이터를 왜 이렇게 쓸까가 자료구조의 핵심이 아닐까?
해시를 사용하는 이유는 크게 세가지로 나눌 수 있다.

• 적은 리소스
• 속도
• 보안

지금부터 왜 해시가 이런 특징을 가지게 되었는지 알아보자.

Hash, Hashing, Hash Function

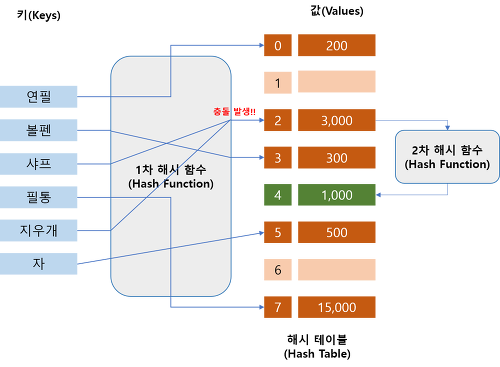
해시는 해시함수를 이용해서 어떤 특정한 값으로 변환시킨다.
이 작업은 해싱이라고 하는데

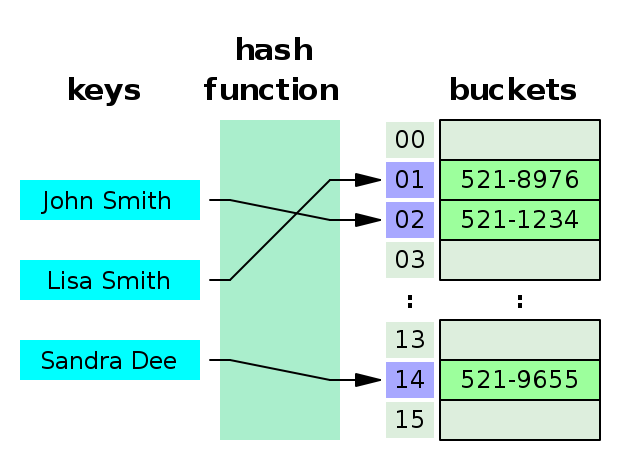
그림과 같이 들어온 값을 해시 함수를 이용해 변환 시킨다.
이런 해시 기법을 이용하여

• 해시 테이블
• SHA(Secure Hash Algorithm) 암호화
• 데이터 압축

에 사용할 수 있고 그 중에서 우리는 자료구조-탐색과 관련있는 해시 테이블에 대해서 공부한다.

Hash Table

해시 테이블은 해시를 이용하여 구현된 자료구조로 다음과 같은 특징이 있다.

• 연관 배열 구조 (Key : Value)
• 빠른 연산 속도 (삽입, 삭제, 탐색 $O(1)$)
• 고정된 테이블 크기, 해시 함수로 인한 해시 충돌 발생 가능
• 해시 충돌 발생 시 연산 속도는 $O(N)까지 느려질 수 있음
• 적은 리소스 사용 (무한한 값 -> 테이블로 나누어진 유한한 해시값)
  이를 통해 KB 단위의 캐시 메모리에서도 데이터를 저장하고 사용할 수 있음
  하지만 크기를 지정해야하기 때문에 공간적으로 효율적인 것은 아님

연관 배열 = Map = Dictionary = Symbol Table

• KEY : VALUE는 매핑된다.
• KEY는 유니크하다.
• KEY와 VALUE를 저장할 수 있다.
• KEY를 통해 VALUE를 알 수 있다.
• KEY를 통해 새 VALUE로 변경할 수 있다.
• KEY를 통해 VALUE를 삭제할 수 있다.

해시 테이블 구조

• Keys
  입력되는 무한하면서 고유한 값이다.
  그런데 만약 해시가 없이 키를 지정하게 된다면 키의 길이에 따라 저장소를 만들어야하기 때문에 해시를 이용하여 무한한 값에서 유한한 값으로 변경한다.

• Hash Function
  해시를 만들기 위한 함수로

  • 암호학적 해시 함수 (SHA, MD5)
  • 비암호학적 해시 함수 (CRC-32)
    와 같은 함수들을 이용하여 해싱한다.
    하지만 다른 key임에도 동일한 해시가 만들어지는 해시 충돌(Hash Collision)이 발생할 수 있어 이러한 충돌 확률을 함수는 최대한 낮춰야 한다.

• Hash
  키가 해싱된 값으로 정확히는 값이 아닌 bucket과 매핑되어 있다.

• Values
  bucket에 저장되어 있는 값이다.

• Buckets(slot)
  해시와 매핑되어 있어 값을 저장하고 있다.

해시 테이블의 동작

해시 테이블은 해시로 만들어진 자료구조로 다음 연산을 수행한다.

• Insertion
• Deletion
• Searching

해시 테이블은 이 세가지 연산에서 모두 O(1)의 속도를 가진다.

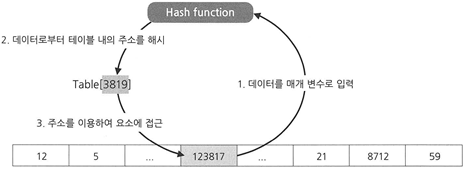
이는 해시 테이블이 그림과 같은 동작을 거치기 때문인데

• 형성된 테이블에서 키를 받는다.
• 키를 해싱하고 해당 해시 저장소에 간다.
• 저장, 삽입, 탐색

실제로 탐색은 해싱이 이루어진 해시값을 찾아가는 탐색뿐으로 크기가 크든 작든 한번의 탐색이 이루어져 마치 배열과 같이 동작한다.

해시 테이블의 크기

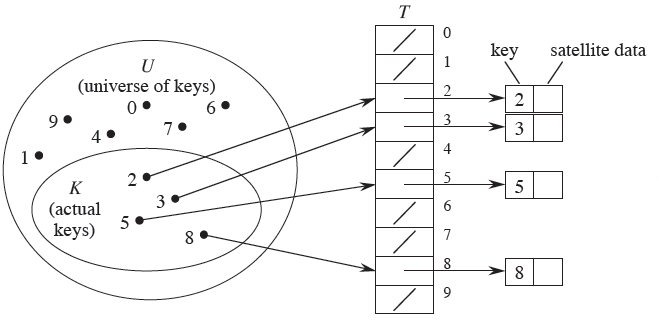
• 해시 테이블은 크기를 지정해줘야 한다
• 입력될 키와 해시 테이블의 크기가 동일하면 충돌 문제가 발생하지 않는데
  이걸 Direct Address Table이라고 한다.
• 하지만 10개의 키에 맞춰 10의 크기를 가진 테이블을 생성했는데 실제로 5개의 키만 사용한다면 그만큼의 메모리 공간을 낭비하게 되고 실제로 테이블의 크기는 키의 개수보다 작게 만든다.
  따라서 해시 충돌은 필연적으로 발생할 수밖에 없다.

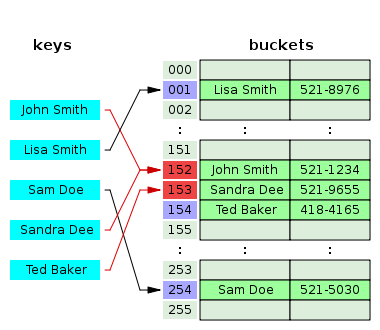
해시 충돌

이렇게 좋은 해시 테이블도 무한한 값을 유한한 해시값으로 변환 시키는 것이기에 Hash Collision의 문제가 있다.
해시 충돌은 다른 키임에도 동일한 해시값을 가지게 되는 것으로 그림에서는
John과 Sandra가 서로 다른 키임에도 2라는 동일 해시를 가지게 됐는데 이러한 해시 충돌 문제는 해시의 기본 원칙인 해시값은 중복되지 않는다를 위배하므로

• Separate Chaning
• Open Addresssing

을 이용하여 해결한다.

Separate Chaning(분리 체이닝)

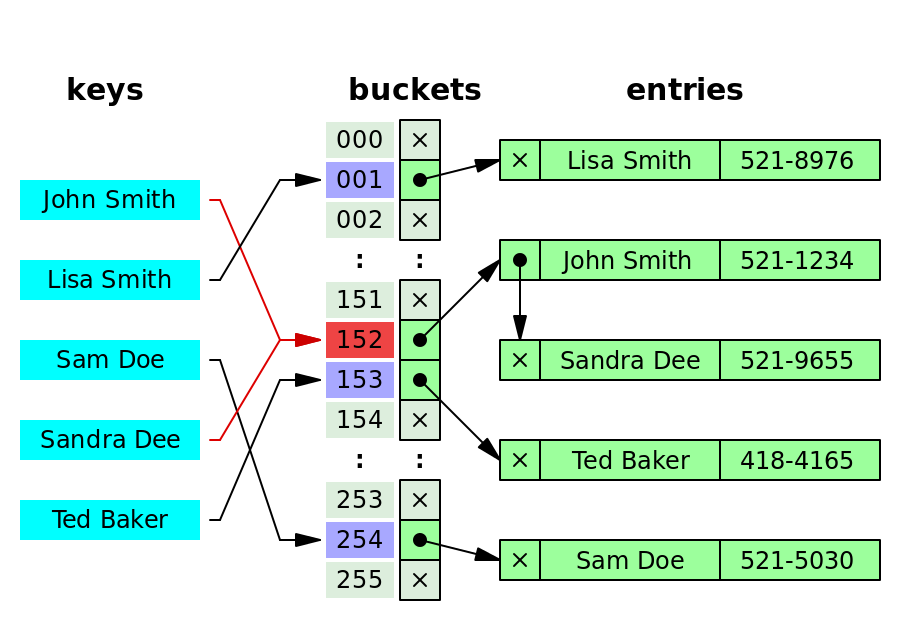
동일 해시값을 유지하고 해결하는 방식으로

• 폐쇄 주소 형식(내가 받은 해시값 이외 접근 불가)
• 해시함수에 대한 충돌 예방에만 집중하지 않아도 됨
  충돌이 일어나더라도 값을 연결시키면 된다.
• 일반적으로 Linked list를 통해 구현
• bucket은 리스트의 포인터를 저장하기 때문에 리스트가 될 별도의 메모리를 사용해야 함
• 값이 없다면 헤드로, 값이 있다면 헤드의 앞에 삽입
• 연산 속도는 $O(1)$이지만 탐색 데이터가 tail에 있다면 $O(N)$까지 늘어남
  데이터가 하나의 bucket에 집중되면 발생하는 일인데 이것도 개선 방법이 있다.
  • 균형 이진 탐색 트리의 사용
    Linked list를 통해 구현되면 마지막 데이터는 $O(N)$의 속도를 가지기 때문에
    탐색과 삭제를 위해 균형 이진 탐색 트리를 구성한다.
    데이터가 아무리 많이 연결되더라도 최소 $O(logN)$의 속도를 보장할 수 있다.

Open Addressing(공개 주소)

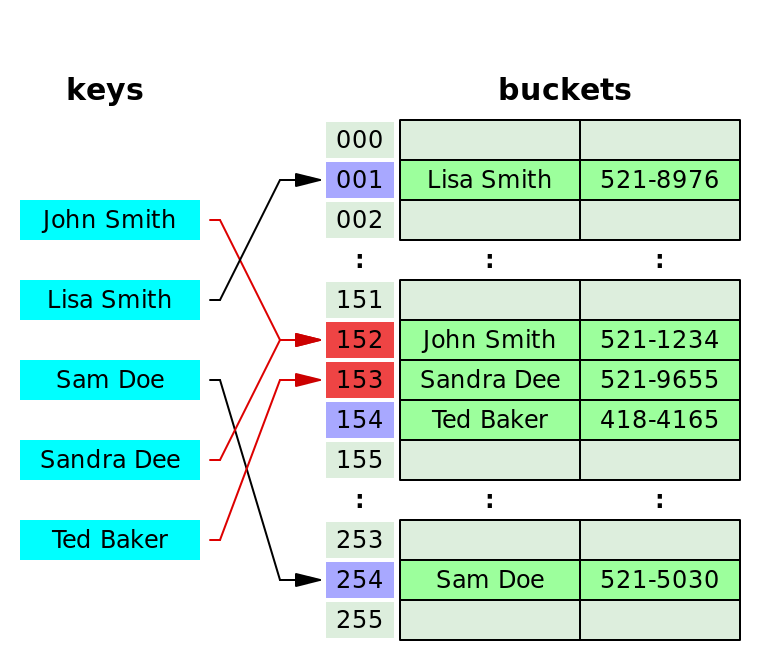
해시 충돌 발생 시 비어있는 해시를 찾는 방식으로 그림에서는 John과 충돌이 발생한 Sandra는 153, Sandra와 충돌이 발생한 Teds는 154로 자신이 받은 해시와 다른 bucket에 데이터를 삽입했다.

• 공개 주소 형식
• 탐색 방식
  공개 주소는 해시 충돌 시 비어있는 bucket을 찾기 위한 탐색이 필요하다
  • Linear Probing(선형 탐사)
  • Qudratic Probing(제곱 탐사)
  • Double Hashing(이중 해싱)
• Linear Probing에서 메모리 참조에 대한 공간 지역성을 만족한다

Linear Probing

• 해시 충돌 발생 지점으로부터 n+1씩 버킷을 탐색한다.
• 공간 지역성에 따른 캐싱에 유리하다.
  
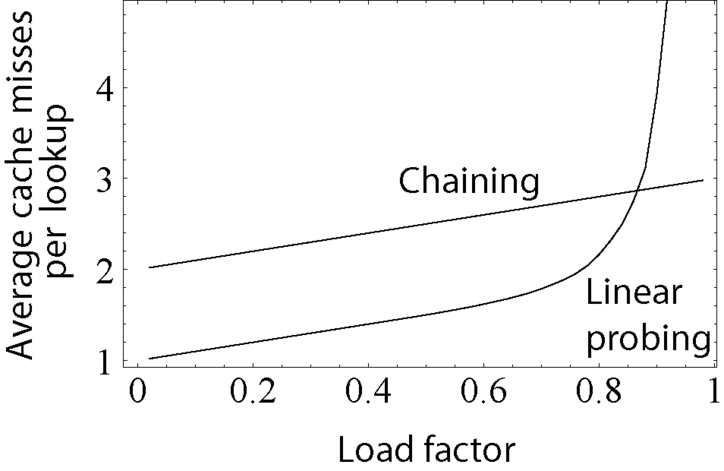
  선형 탐색은 캐싱에 분명히 유리하지만 Load factor(해시 테이블에서 버킷이 가득찬 확률)가 높아질수록 효율이 급격하게 감소한다.

  자바 HashMap은 75 - 80%의 Load factor를 유지한다.

• 주변의 버킷이 전부 차있는 Primary Clustering 문제가 있다.
  
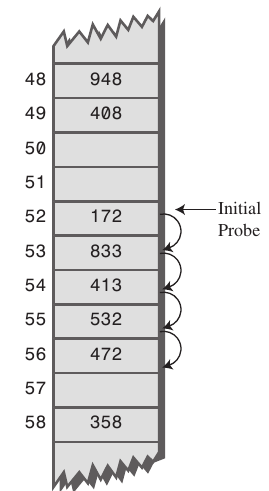
  주변 버킷이 차있지 않았다면 바로 53에 데이터를 삽입할 수 있었지만 Clustering으로 인해 4번이나 이동한 57에 삽입할 수 있다.

Qudratic Probing

• Primary Clustering을 개선하기 위한 방법
• 해시 충돌 발생 지점으로부터 제곱 수에 따라 탐색 범위를 확장시킨다.
• 초기 해쉬값이 동일하다면 탐색 범위도 동일한 Secondary Clustering 문제가 있다.
  
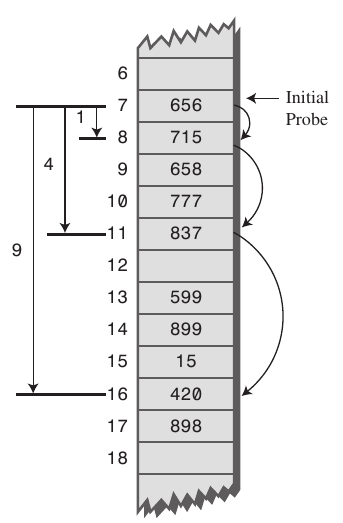
  초기 발생 지점 7에서 $1*2$ 지점 충돌 발생, 다음 범위로 넘어간 $1 * 4$ 지점 충돌 발생, 12 삽입 못하고 다음 범위로 .... 이런 일은 다른 키가 동일 해시값을 가질 시 똑같이 일어난다.

Double Hashing

• 앞선 탐색들이 규칙성을 가져 Clustering문제가 발생한다면 규칙성을 없애자는 방식
• 하나의 해시값은 데이터를 저장할 bucket이 되고, 다른 해시값은 앞선 해시값을 통해 탐색 범위를 만들 해시값이 된다.
  

Bucket Overflow의 개선

• Open Addressing 방식을 사용 시 버킷 탐색에 따라 범위를 넘어가는 Bucket Overflow 발생 가능
• 버킷의 개수를 늘려 해결할 수 있다.
  • Bucket Resizing & Rehashing
    하지만 버킷의 개수를 늘리기 위해 새 버킷을 생성하는 건 비용이 큰 작업이다.

Java HashMap

자바는 HashTable과 Collection Framework인 HashMap을 통해 해시 테이블을 제공한다.
해시 테이블의 관건은 어떻게 해시 충돌을 줄일지가 핵심인데 HashMap은 Additional Hash Function을 사용하여 그렇지 않은 HashTable보다 성능 상 이점이 있어 하위 호호환성을 제외하곤 HashMap이 많이 쓰이고 있다.

객체 키에 대한 해시 충돌

• 객체에 대한 해시 값은 object x.hashCode()로 사용한다.
• Boolean, Integer와 같은 값들은 해시와 해시를 비교할 수 있다.
  (x.equals(y) == false이고 x.hashCode() != y.hashCode()가 성립할 때 완전한 해시 함수라고 한다)
• String이나 POJO에 대해서는 위 조건이 성립되지 못한다.
• hasCode()가 반환하는 해시값은 int형이고 이에 따라 해시 충돌을 막으려면 int 크기만큼의 해시 테이블이 필요하다.
• 메모리 효율성을 위해 인덱스는 실제로 hashCode() 값을 나누어 사용하고 이는 반드시 해시 충돌이 일어난다.

HashMap의 해시 충돌 해결

Java HashMap에선 Separate Chaing을 사용하는데 이는 Open Addressing의
Clustering에 따른 삭제, 탐색 연산이 비효율적이고 Separate Chaining이 충돌을 줄이고 충돌 시 발생한 체인에 대한 속도를 잘 조정한다면 더 효율적이기 때문이다.

Java 8 Separate Chaining

• 기존 체이닝은 링크드 리스트의 문제점을 그대로 가지고 있다.
• 자바 8에서는 하나의 버킷에 상수를 통해 6개 이하의 데이터라면 링크드 리스트를 사용하지만 8개 이상의 데이터가 쌓이면 이를 Red-Black 트리로 변환한다.
  이에 따라 연산에 대한 최악의 경우에도 $O(logN)$의 속도를 보장할 수 있다.

  Java 8 HashMap
  static final int TREEIFY_THRESHOLD = 8;
  static final int UNTREEIFY_THRESHOLD = 6;

해시 버킷 동적 확장

• 해시 버킷은 항상 키보다 적기 때문에 충돌이 발생한다.
• HashMap은 entry가 일정 개수 이상되면 해시 버킷 크기를 두배씩 늘려 최대 $2^30$까지 늘린다.
• 해시 버킷의 확장(Resizing) 시 재해싱을 통해 데이터를 삽입해야하는데 이는 HashMap의 생성자를 통해 초기 크기를 지정하여 막을 수 있다.
  하지만 HashMap의 버킷 개수가 많아질수록 수행 시간은 계속해서 늘어나고 크기가 $2^n$이 되기때문에 2의 승수에 의한 해시충돌이 쉽게 발생한다.

HashMap Additional Hash Function

이런 해시 버킷 확장에 대한 문제를 해결하기 위해 보조 해시 함수가 사용되는데
해시 인덱스를 균등하게 분포하여 해시 충돌을 줄이는데 목적을 둔다.
하지만 보조 해시 함수는 Java 8에서 정말 간단해졌는데 이는 충돌이 발생하더라도 Seprate Chaing에서 Red-Black 트리를 사용하고 해시 함수 자체가 균등 분포를 잘 구현하고 있기 때문이다.

32비트 중 상위 16비트값을 XOR 연산
static final int hash(Object key) {
int h; return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

결론

• Hash를 이용한 HashTable은 적은 리소스, 속도, 보안이라는 관점에서 매우 좋은 자료구조다.
• 현실세계에서 들어오는 데이터(키)는 랜덤하지 않다.
  그런 키들이 들어오더라도 해시함수는 충돌을 줄일 수 있어야한다.
• HashTable은 해시 충돌이라는 문제점을 가지고 있고 이는 Seprate Chaining과 Open Addressing을 통해 개선할 수 있다.
• 자바 HashMap에서는 Seprate Chining을 사용하며 Red-Black 트리를 통해 그 단점을 개선했다.

참고

고니 블로그
adam2 벨로그
ratsgo 블로그
카니 블로그
조대협 블로그
Naver D2
영문위키