목표

• Quick Sort 알고리즘 이해
• Quick Sort 알고리즘 구현
• Quick Sort 알고리즘 특징과 시간복잡도 이해

Quick Sort 알고리즘

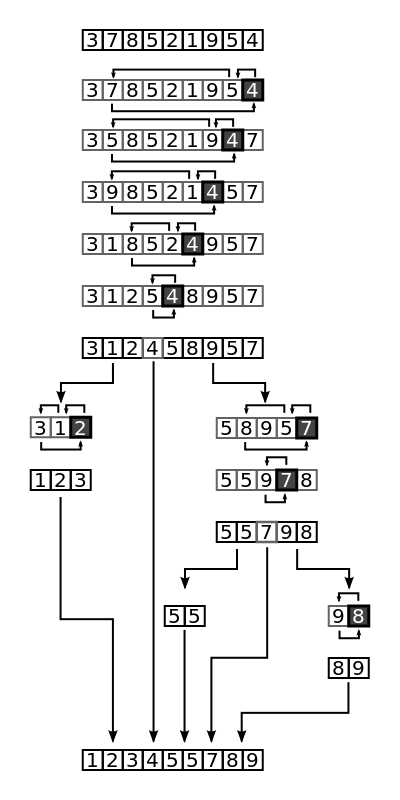
• 가장 효율적인 정렬 알고리즘
• divide and conquer(분할정복) 기법을 사용
• merge sort와 다르게 분할정복 후 합병이 필요 없음
• pivot을 통해 data <= pivot <= data 방식으로 정렬
• 비교 정렬
• 불안정 정렬(데이터의 상대적 순서가 유지되지 않음)
• 최악의 경우 O(n²)까지 시간복잡도가 증가
  편향 링크드 리스트의 검색 속도와 동일해짐

Quick Sort 알고리즘 구현

구현법

1. pivot 선택하기(left, right, mid)
2. pivot을 기준으로 분할하기
   pivot 보다 작은 수는 전방으로, 큰 수는 후방으로 정렬(파티셔닝)
3. 재귀호출을 통해 전방, 후방 정렬

Right Pivot Quick

public static int partition(Integer[] arr, int left, int right) {
        int i, j, x;
        i = left - 1; // -1
        j = left; // 0
        x = arr[right]; // pivot
        while (j <= right - 1) { // pivot - 1까지 순회
            if (arr[j] <= x) { // pivot보다 작은 값이면
                ++i; // i 증가 시키고 스왑
                swap(arr, i, j);
            }
            j++; // j 증가
        }
        swap(arr, i + 1, right); // pivot보다 작은 값만 앞에 남았으니 스왑
        return i + 1; // 새 pivot 결정
    }

• 입력 : 8 5 20 3 15 1 4
• 분할 : 3 1 4 8 15 5 20
• 재귀 : 1 3 4 8 15 5 20
• 분할 : 1 3 4 5 15 8 20
• 재귀 : 1 3 4 5 8 15 20
  right = pivot - 1 = 3 반환
  if(left < right) 불만족으로 재귀 종료
• 1만개 데이터 수행시간 0.003초
• 5만개 데이터 Stack overflow

Left Pivot Quick

• 교차방식 쓰니까 어렵다.
• 각 글들을 참고하여 다시 Quicksort의 조건을 세웠다.

1. Recursion 탈출 조건은 Left < Right
2. Left부터 배열의 끝(Right)까지 비교할 수 있는 loop
3. 첫 분할 시 피벗을 기준으로 작은 값은 left, 큰 값은 right
   while(arr[i] <= pivot) left++
   while(arr[j] >= pivot) right --
4. j-- 시 배열의 시작점을 넘어가지 않도록 조건
5. i와 j가 서로 교차하지 않고 값을 찾았다면 swap
6. i와 j가 서로 교차했다면 left와 j교환
7. 새 피벗이 될 j 반환
8. Recursion

전체 코드

    public static int partition(Integer[] arr, int left, int right) {
        int i = left;
        int j = right;
        while (i < j) {
            while (arr[left] > arr[i]) { // pivot 비교
                i++;
            }
            while (arr[left] <= arr[j] &&  i < j) { // pivot 비교, 인덱스 조건
                j--;
            }
            if (i < j) {
                swap(arr, i, j);
            }
        }
        swap(arr, left, j);
        return j;
    }

• 1만개 데이터 수행시간 0.138초
• 각 포인터가 같이 움직이는게 아니라 최적화 된 코드에 비해 많이 느리다.

Mid Quick

• 데이터의 정렬이 매번 랜덤한 문제점
• 나만 실패한줄 알았는데 실패한 사람들이 많은거보니 효율적인 방법이 아닌듯?
• Median of Three 방식을 이용해야할듯

Linked list Quick

전체코드

public void quickSort(Node left, Node right) {
        //  재귀 탈출 조건 
        if (right != null && left != right && left != right.next) {
            Node temp = partition(left, right);
            quickSort(left, temp.prev);
            quickSort(temp.next, right);
        }
    }

    Node partition(Node left, Node right) {
        int pivot = right.data; // 우측 끝을 피벗으로 설정
        Node i = left.prev; // 리스트의 시작 설정 배열로 치면 left - 1
        // 배열에서 for(int j = left; j <= right - 1; j++) 과 같음
        // 첫 리스트부터 끝 리스트까지 순회
        for (Node j = left; j != right; j = j.next) {
            if (j.data <= pivot) {
                // 피벗이 작으면 i++과 같음
                i = (i == null) ? left : i.next;
                // 아니라면 swap
                swap(i, j);
            }
        }
        // 탈출 시 여전히 조건을 만족 한다면
        i = (i == null) ? left : i.next;
        swap(i, right);
        return i;
    }

• 리스트다보니 피벗도 노드로 반환하는 점이 재밌었음
• 글들을 참고하며 배열 순회와 뭐가 다른지 비교하는 점도 재밌었음

Quick Sort 알고리즘 특징과 시간복잡도

• 공간에 최적화 된 이진 트리 정렬
  실제 트리가 아닌 재귀호출에 의한 가상 트리를 통해 정렬 (재귀 콜스택)
• 알고리즘은 정확히 동일한 비교를 수행하지만 순서는 미보장 (불안정 정렬)
  4a 5b 1a 1b 3a 2a라는 데이터가 있다면 이 데이터는 ASC 정렬 시
  1b 1a 2a 3a 4a 5b로 상대적 순서를 보장하지 않고 정렬될 수 있음.
• 연결리스트를 사용하여 안정적인 정렬로 구현 될 수 있지만 피벗을 잘못 선택하는 경우가 존재
• 순차정렬 된 자료, 피벗이 최대/최소값 정렬된 자료에서 O(n^2)까지 시간이 늘어날 수 있음
• Quicksort vs. Heapsort
  힙 소트의 실행 시간은 O(n log n)이지만 힙 소트의 평균 시간은 퀵 소트의 평균보다 느림.
• Quicksort vs. Mergesort
  퀵과 힙 정렬과 달리 안정적인 정렬 방식으로 Mergesort는 최악에서도 가장 빠른 속도를 가짐.

문제점과 개선

문제점

• 선택한 피벗이 최대값이나 최소값이면 정렬시간은 Worst case O(n²)
• 데이터 크기에 따른 재귀 스택 증가로 인한 Stack overflow

개선

핵심은 어떻게 가장 중간값에 가까운 pivot을 찾을 것인가?

• Median of Three(세개의 중간값 찾기)
  left, mid , right 를 계속 비교하여 피벗의 중간값을 선택
  끝과 끝은 어차피 가장 작거나 가장 크니 계속 비교하면 중간을 알 수 있다.
  최악의 경우에도 O(n)을 보장하고 스택 깊이가 줄어들기 때문에 Stack overflow에 상대적으로 안정적
• 3-Way Partition
  파티션을 3개로 분할해 중복값을 중앙으로 모으는 방법이지만 파티션을 3개로 분할함에 따라
  지역성에 불리하고 스왑이 많음
• No Recursion
  재귀를 사용하지 않는 방법으로 자체 스택을 생성하여 Stack overflow 예방
• Rnadom Pivot
  최대값과 최소값이 선택되서 문제가 발생한다면 랜덤한 피벗을 선택하여 가장 평균에 가깝게 만드는 방법

구현

Median of Three

public static void quickSort(Integer[] arr, int left, int right) {
        int mid = (left + right) / 2;
        int pivot, i, j;
        threeSort(arr, left, right, mid);
        if (right - left + 1 > 3) {
            pivot = arr[mid];
            swap(arr, mid, right - 1);
            i = left;
            j = right - 1;
            //System.out.println("pivot = " + pivot);
            while (true) {
                while (arr[++i] < pivot);
                while (arr[--j] > pivot);
                if (i >= j) {
                    break;
                }
                swap(arr, i, j);
            }
            swap(arr, i, right - 1);
            //System.out.println("arr = " + Arrays.deepToString(arr) + ", left = " + left + ", right = " + right);
            quickSort(arr, left, i - 1);
            quickSort(arr, i + 1, right);
        }
    }


    public static void threeSort(Integer[] arr, int left, int right, int mid) {
        if (arr[left] >= arr[mid]) swap(arr, left, mid);
        if (arr[left] >= arr[right]) swap(arr, left, right);
        if (arr[mid] >= arr[right]) swap(arr, mid, right);
    }

• 수행시간 0.003초
• 5만개 데이터 기준 0.028초
  재귀 스택이 최대 절반까지 줄어들기 때문에 Stack overflow 발생하지 않음

Random pivot

public static int partition(Integer[] arr, int left, int right) {
        Random r = new Random();
        int pivot = r.nextInt(right - left) + left;
        System.out.println("pivot = " + pivot);
        int i = left;
        int j = right;
        swap(arr, left, pivot);
        System.out.println("arr = " + Arrays.deepToString(arr) + ", left = " + left + ", right = " + right);
        while (i < j) {
            while (arr[left] > arr[i]) { // pivot >= data
                i++;
            }
            while (arr[left] <= arr[j] && i < j) { // pivot <= data, outOfIndex
                j--;
            }
            if (i < j) { // swap
                swap(arr, i, j);
            }
        }
        swap(arr, left, j); // pivot swap
        System.out.println("arr = " + Arrays.deepToString(arr) + ", left = " + left + ", right = " + right);
        return j;
    }

• 범위안에서 랜덤하게 피벗을 가져올 수 있게만 추가해주면 된다.
• 근데 피벗 인덱스가 왜 출력이랑은 다른건지 모르겠다.

결론

• Quick sort는 O(n log n)의 평균적으로 시간을 보장
  피벗이 최대, 최소값일 경우에는 O(n^2)까지 추락
• 불안정 정렬로 데이터의 상대적 순서는 보장하지 않음
• 피벗을 중간으로 잡느냐 잡지못하냐에 따라 알고리즘의 속도를 결정
  이에 따라 Median of Three, Random Pivot을 통해 개선
• 재귀에 따라 콜 스택이 증가하며 Stack Overflow가 발생하는 단점
  자체 스택을 구현해 힙 영역을 사용하여 개선
• 정렬 알고리즘의 속도를 결정하는 건 참조의 지역성 원리인데 이에 따라 효율적임

  시간 복잡도가 $O(nlogn)$이라는 말은
  실제 동작 시간은 $C×nlogn+α$라는 의미이다.
  상대적으로 무시할 수 있는 부분인 $α$ 부분을 제하면 $nlogn$에는 앞에 $C$라는 상수가 곱해져 있어 이 값에 따라 실제 동작 시간에 큰 차이가 생긴다.
  이 $C$라는 값에 큰 영향을 끼치는 요소로 '알고리즘이 참조 지역성(Locality of reference) 원리를 얼마나 잘 만족하는가'가 있다.
  (Naver D2 Tim sort 발췌)

어려운면서도 어렵던 정렬이였다.

참고

영문 위키
퀵소트 vs 힙소트
합병,힙 vs 퀵소트
바킹독
프린스턴
퀵소트 정리
퀵소트 파헤치기
퀵소트 문제점
Doubly Linked list