목표

• Union Find를 이해한다.
• 자바 Union Find의 구현을 알아본다.
• Union Find 개선을 알아본다.
  • Path Compression(경로압축)
  • Union By Rank (Weigted Union)
• Union Find 시간복잡도를 알아본다.

Union Find

• Kruskal's Algorithm 구현을 위한 핵심 자료구조
• Compare Set(집합 비교), Find(합집합 찾기), Uinon(합집합)의 연산을 수행하기 때문에 Union-Find라고 함.
• 배열과 트리를 사용해서 구현

구현

• 집합의 각 원소들이 트리의 노드
• 루트와 부모는 중요하지 않음
• 트리의 각 노드는 부모의 노드 주소를 가짐(상향식)
  상향식 트리이기에 하나의 부모만 가지고 일반적 트리보다 간단한 구조를 가짐
  하나의 일차원 배열로 표현 가능

Union Find

function Find(x)
   if x.parent ≠ x
     x.parent := Find(x.parent)
   return x.parent

• Find set
  자신이 속한 트리와 비교해서 같은 집합인지 확인
  • 동일하면 그냥 반환
  • 같지 않으면 재귀를 돌며 루트까지 확인
    최악의 경우 $O(N)$

-Union
트리를 구성하는 건 $O(1)$이지만 루트를 찾아가는 건 동일한 $O(N)$임

Union Find 개선과 시간복잡도

• find와 union의 $O(N)$연산이 union find의 주요 요점
• 트리의 높이에 시간 복잡도가 정해짐
  트리의 높이를 가능한 낮게 어떻게 만들 것인가?

Weighted Union

• 두 집합을 union할 때 작은 트리의 루트를 큰 트리 루트의 자식으로 만듬(노드 개수)
  작은 트리가 큰 트리로 들어가면 높이는 변하지 않음
• 각 트리의 크기(노드 개수)를 카운트 해서 체크
  
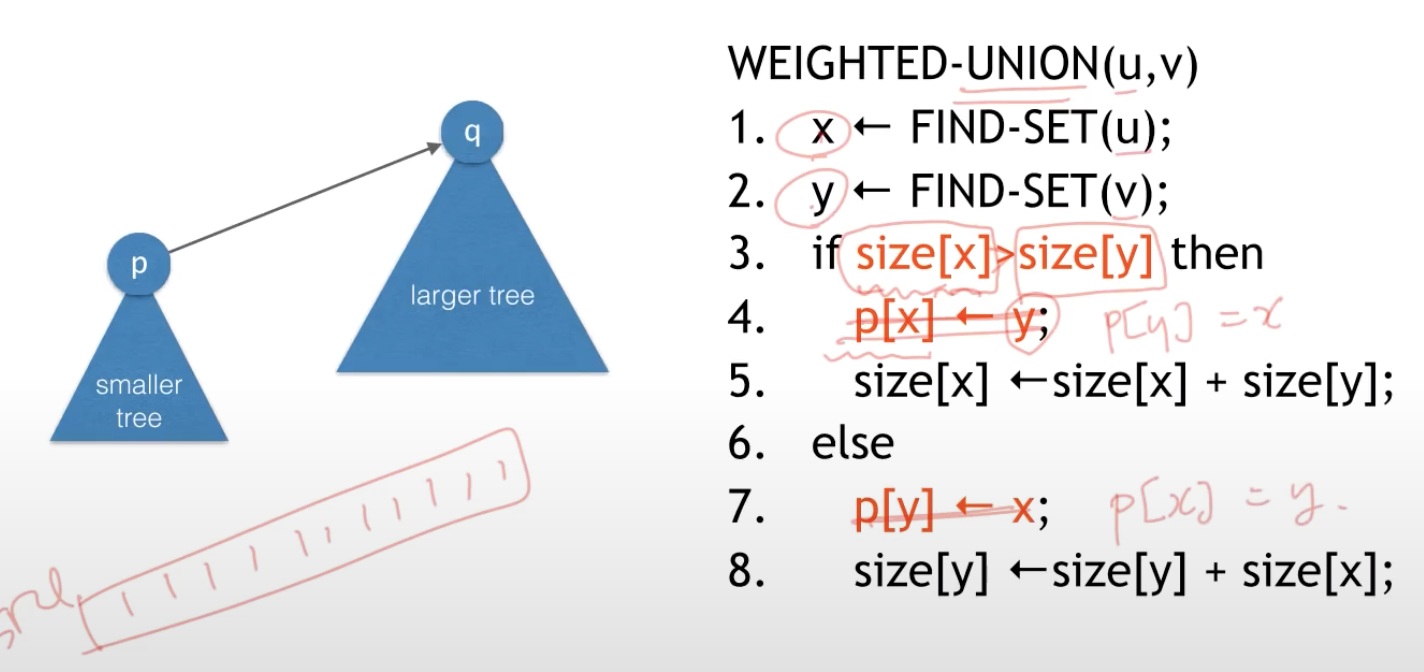
• 내 집합의 레벨이 작을 때만 트리의 레벨이 증가한다.
  --> 레벨이 $h$라면 노드는 $2^h$ 증가했다.
  --> 즉 어떤 노드 n이 가질 수 있는 레벨 최대값은 $O(logn)$
• 또는 높이를 계산해서도 들어갈 수 있음
  경로 압축을 같이 쓰면 경로 압축에 의해 높이는 루트로부터 최대 2까지밖에 안나오기때문

    public void rankUnion(int x, int y) {
        x = find(x);
        y = find(y);
        // 동일 루트면 종료
        if (x == y) {
            return;
        }
        // 트리 x보다 y가 작다면 x를 작게 만듬
        if (rank[x] > rank[y]) {
            tree[y] = x;
        } else { // 반대면 반대로
            tree[x] = y;
        }
        // 만약 트리 둘의 레벨이 같다면 union 됐으니 레벨 1 증가
        if (rank[x] == rank[y]) {
            rank[x]++;
        }
    }

• u.rankUnion(5, 7);
  u.rankUnion(3, 2);
  u.rankUnion(4, 2);
  u.rankUnion(1, 5);
  u.rankUnion(4, 7);
  7 7 2 2 7 6 7
• u.find(4);
  u.find(3);
  7 7 7 7 7 6 7

Path Compression(경로 압축)

• Find 단계에서 할 수 있는 개선법
• 트리가 높이가 최대치인 경우
  
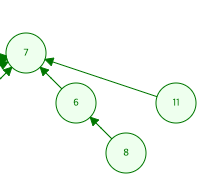
  이때 8을 찾기 위해선 8 -> 6 -> 7로 가서 루트 7을 받아올 수 밖에 없음
  근데 8이나 6이나 루트는 7로 같음
  그렇다면 6을 거치지 않고 루트로 갈 수 있도록 만들어주면 됨.
  
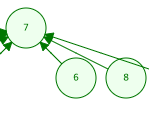
  이렇게 되면 한번에 찾을 수 있으므로 $O(1)$

public int find(int x) {
        if (tree[x] == x) {
            return x;
        }
        // Path Compression
        return tree[x] = find(tree[x]); // 인덱스 6, 7, 8 = 7
    }

시간복잡도

• 경로는 절반씩 압축되기 때문에 노드가 4개일 때는 2번, 16개일 때 3번, 65536개가 되야 4번, $2$^65536이 되야 5번
• 따라서 find에 걸리는 시간은 언제나 $O(4)$ 아래
  이는 거의 선형 시간에 가깝다.
  
  Weight Union과 Path Compression을 사용했을 때
• 모든 정점을 초기화 하는데 걸리는 시간 $O(m)$
• 에지들을 정렬하는데 걸리는 시간 $O(eloge)$
• Find(path compression)은 $O(1)$
  Union(Weighted Union)은 $O(M)$

하지만 M(에지 개수)는 항상 $N-1$개 이기때문에 이를 $(n^2)$으로 치환가능하고 이는 $O(elogn)$이 된다.
결국 시간복잡도는 $O(정점log에지)$가 된다.

참고

영문 위키
권오흠 알고리즘