목표

• DAG(Direct Acyclic Graph)를 이해한다.
• Topologicial Ordering(Sorting)을 이해한다.

DAG 비순환 방향성 그래프

• 방향성만이 존재하는 그래프로 순환이 없으며 절대 다시 뒤로 돌아올 수 없다
• 모든 노드들을 방문할 수 없다
  방향은 중복되지 않고 한 정점에 한방향만 존재
• 어떤 트랜잭션(연산)에 대해 선행관계를 따지는데 매우 유용한 구조
  
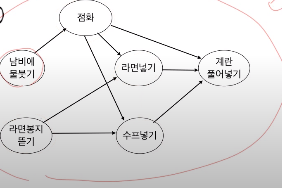
  만약 라면 끓이기라는 작업에 대해 분산된 트랜잭션들이 존재한다면
  냄비와 봉지라는 트랜잭션에 대해서는 서로 선행관계가 없지만 라면을 넣는다는 트랜잭션 전에는 반드시 냄비를 준비하거나 라면을 먼저 준비해야 한다.

이러한 특징에 따라 DAG는 서로 간 연산에 따른 순서가 필요한 작업들
스프레드(엑셀) 시트의 수정 연산, 네트워크 흐름, 전자 회로 등 서로 간의 데이터 흐름에 따른 순서 즉 스케쥴링을 가지는 작업들에 사용할 수 있다.

위상정렬 Topologicial Ordering

그렇다면 이 순서들을 각 정점에 따라 어떻게 정렬할 것인가?
이게 바로 Topologicial Ordering(Sorting)이다.

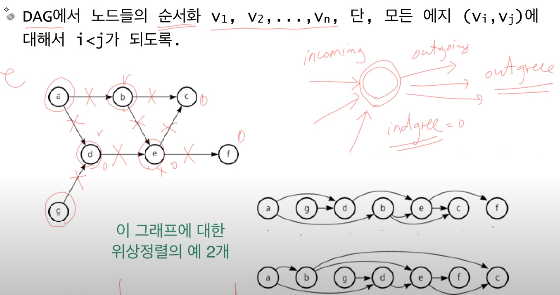
• 각 정점들은 방향성 에지에 대해 ingoing/outgoing degree를 가진다
• 이 indegree와 outdegree를 통해 순서를 정렬한다
• 그래프의 순서화는 하나로 보장되지 않는다

에지 제거 구현법

이 구현법에서는 맨 처음에 들어간 노드가 맨 처음에 나와야 되고
그 노드에 연결 된 outdegree를 제거해야하기 때문에 Queue를 사용해야한다.
1. indegree가 없는 노드를 검색하고 출력한다
2. 출력한 정점과 에지를 제거한다
3. 1번을 반복한다
이렇게 되면 처음 indegree가 없던 정점이 제거되고, 제거된 정점이 가지고 있던 다음 정점은 indegree가 없는 정점이 된다.
이 반복은 최악의 경우 모든 노드 $n$과 에지 $n-1$ 대하여 이루어지므로 $O(n+m)$이 된다.

꼬리 물기 구현법

DFS를 통해 정점을 순회 하고 리스트 형식으로 정점을 묶는다
DFS가 종료되면 리스트에 정점이 꼬리 물기식으로 물려짐
DFS를 사용하기 위해 Stackd을 사용