목표

• 최소 스패닝 트리를 구현할 수 있는 프림 알고리즘을 이해한다.

프림 알고리즘

• 정점 탐색 기반
• Greedy(탐욕스런) 기법 사용
• 각 정점의 가중치를 비교하기 때문에 정점의 수가 적을수록 유리
  정점보다 간선의 수가 많은 Dense Graph에서 유리하다.

프림 알고리즘 구현법

1. 정점들 중 가중치가 가장 낮은 정점을 선택한다.
2. 시작 정점과 인접한 정점들의 가중치를 비교하여 가장 낮은 가중치와 연결한다.
   이 때 사이클이 형성 된다면 가중치가 낮더라도 제외한다.
3. $N$개의 노드를 채울 때까지 반복한다.

프림 알고리즘이 어떻게 MST를 만족할까?

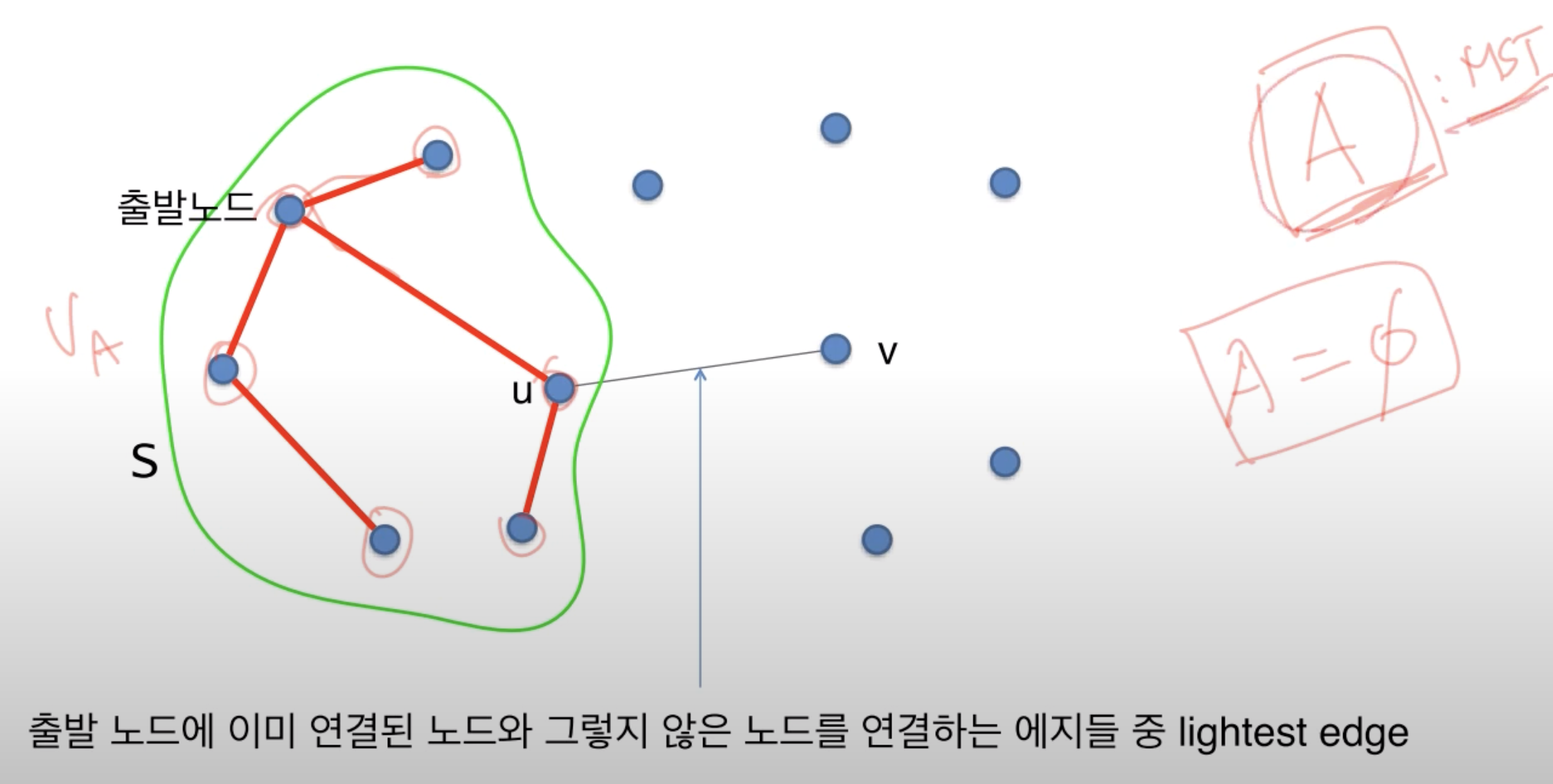
• 기존 크루스칼 알고리즘과 비슷하게 프림 알고리즘으로 구성 된 정점 집합 V와
  그렇지 않은 집합 $V-S$가 존재
• $V-S$는 $V$의 어떤 정점과도 Cross하지 않으므로 Respect
• 따라서 두 집합 사이에서 가장 가중치가 낮은 어떤 정점을 연결하는 것은 어떤 에지를 연결하는 것과 같고 이는 크루스칼 알고리즘에서 증명 됐듯이 MST 형성 조건을 위배하지 않는다

프림 알고리즘 시간복잡도와 개선

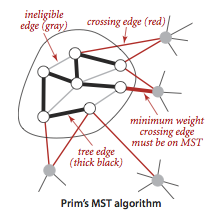
프림 알고리즘은 정점 선택을 기반으로 최소 비용의 트리를 구성한다.

시간복잡도

• 모든 정점의 초기화 $O(N)$
• 최악의 경우 시작 정점 집합과 그렇지 않은 집합의 모든 노드를 탐색 $O(n^2)$
  
  여기에 $n-1$개의 에지까지 추가 한다면 Lazy Prim 구성 시 최악의 경우 $O(n^3)$의 시간복잡도

개선

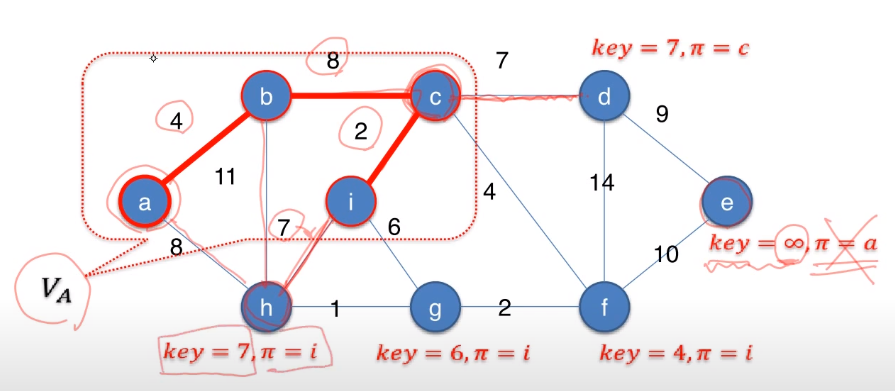
• 정점들에 가중치 값을 추가
• 이렇게 되면 MST에 속하지 않은 정점들 중에서 가중치가 가장 낮은 정점을 선택하여 연결하면 됨
• 연결되지 않은 정점의 수는 많아봐야 $n$개, 따라서 가중치가 낮은 정점의 선택을 $O(n)$까지 줄일 수 있음

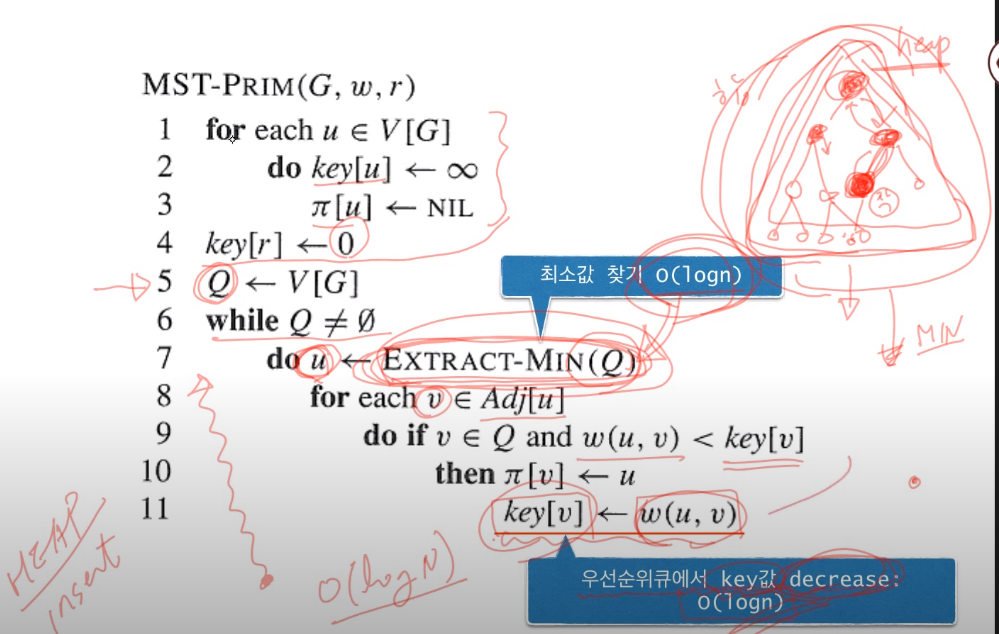
• 그래도 아직 $O(n^2)$의 시간복잡도
• 최소값을 찾는 연산을 줄일 수 있도록 최소 우선순위 큐(최소 힙)을 사용
• 최소 힙은 트리 구조로 연산 속도는 $O(nlogn)$까지 줄일 수 있음

• 따라서 최소 값을 최소 힙으로 연산 $O(nlogn)$하고 $n-1$개의 에지까지 연산을 한다고 하면 에지 연산 $O(n-1)$안에 n이 포함되므로 $n-1$개의 에지를 $m$으로 표시한다면 최종 시간복잡도는 $O(mlogn)$까지 개선할 수 있다.

자바 프림 알고리즘 구현

구현 필요 요소

• Weighted Graph
• Visited[]
• Priority Queue

public ArrayList<edgeSet> prim() {
            // 시작 정점
            // 시작 정점에서 가장 최소치인 간선
            // 방문 안했다면 선택

            PriorityQueue<edgeSet> pq = new PriorityQueue<>();
            Queue<Integer> queue = new LinkedList<>();
            queue.add(graph.indexOf(graph.get(1)));
            ArrayList<edgeSet> mst = new ArrayList<>();

            while (!queue.isEmpty()) {
                int now = queue.poll();
                visited[now] = true;

                for (edgeSet set : graph.get(now)) {
                    if (!visited[set.v]) {
                        pq.add(set);
                    }
                }
                while (!pq.isEmpty()) {
                    edgeSet set = pq.poll();
                    if (!visited[set.v]) {
                        queue.add(set.v);
                        visited[set.v] = true;
                        mst.add(set);
                        break;
                    }
                }
            }
            return mst;
        }

참고

권오흠 알고리즘
영문 위키
프린스턴 대학교 알고리즘