목표

• 그래프에서 최단 경로 우선(Shortest Path First)에 대해 이해한다.
• 벨만 포드(Bellman Ford) 알고리즘을 이해한다.

최단 경로 우선 알고리즘

• 가중치가 있는 그래프에서 정점과 정점 간 최단의 경로를 탐색하는 것
• 보통 방향 그래프를 기준, 무방향 그래프의 경우 양방향으로 에지가 두 개 있는 방향그래프로 보면 됨
• 음수 가중치와 음수 사이클이 있을 수 있음
  
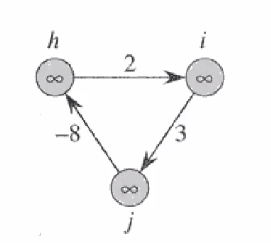
  하지만 음수 가중치는 보통 없다고 상정, 음수 사이클의 경우 무한한 사이클을 유지하는 것이 최단 경로라는 의미기때문에 성립 불가
• 최단 경로는 부분 경로를 포함함
  
  $u -> v1 -> v2 -> v$
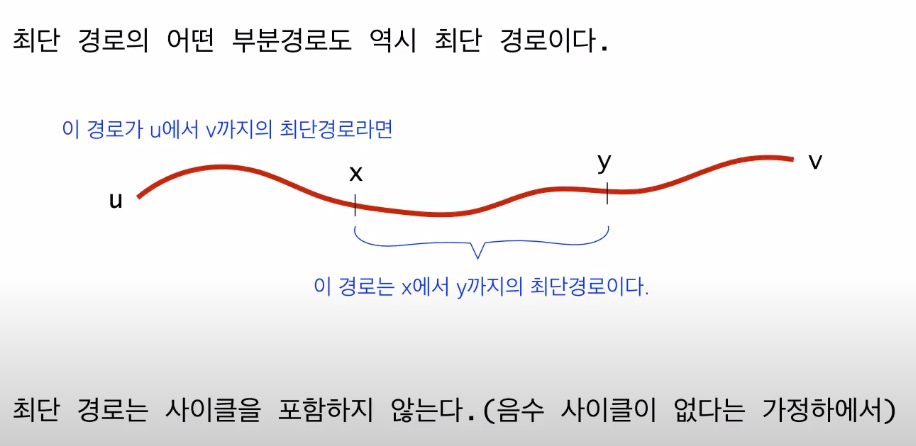
  u와 v가 최단 경로라면 $u, v1$도 최단 경로, $u, v2$도 최단 경로, $v1,v2$도 역시 최단 경로임

최단 경로의 종류

$d(u,v)$라고 가정 시

• Single Source
  One to All, 하나의 시작 정점에서 모든 목적지를 탐색, 다익스트라 알고리즘
• Single Destination
  All to One, 하나의 목적지와 여러 개의 기준 정점, Single Source에서 방향만 토글 시키면 구현 가능
• Single Pair
  One to One, 기준 정점 $s$와 목적지 $v$와의 최단 경로, 이렇게 나온 최단 경로가 최선이 아닐 수 있기때문에 Single Source에 비해 잘 쓰이지 않음
• All Pair
  ALL to ALL, 모든 정점과 모든 목적지를 비교, Floyd-Warshall 알고리즘

최단 경로 우선의 구현

• 최단 경로는 대부분 거리 추정치를 사용함
  맨 처음은 추정치가 무한대, 이후 추정치가 감소
  감소 된 추정치는 결국 $s-v$의 최단 경로가 됨
• 최단 경로의 목적지를 찾았다는 건 최대 n-1개의 에지만 구성하면 되니 직전 노드가 최단 경로의 노드가 됨

Realaxation

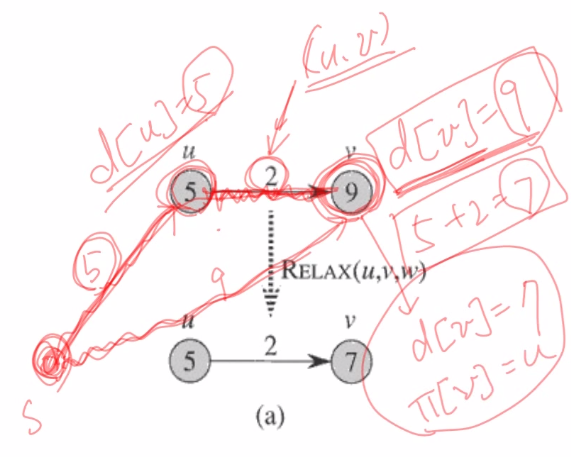
• 기본적으로 최단 경로 우선 알고리즘은 Realaxation 연산을 구현
  1. 시작 정점 $s$가 탐색한 정점 $u,v$가 있다
  2. $d(s,u)$는 5의 가중치, $d(s, v)$는 9의 가중치, $d(u,v)$는 2의 가중치
  3. 그렇다면 정점 $u,v$를 통해 거치는 가중치는 7, $v$를 통한 가중치는 9가 되는데 결국 $s$에서 $v$를 간다는 것은 부분 경로를 포함하기에 7이 된다
  4. 따라서 Realaxation 연산을 통해 가중치를 변경해준다
     앞선 연산 방법에 따라 보면 $d[v] = w(u + v)$ 즉 $7 = 5 + 2$니까 최단 경로 연산이 성공적으로 이루어졌다.

Realaxation 연산은 왜 최단 경로를 구성하는가?

• 그래프에서 에지는 $n-1$개를 가진다
  이는 사이클이 없고, 한 정점은 한번만 거쳐 모든 노드를 탐색
• 모든 노드를 반복하는 것이 Round라고 한다면
  
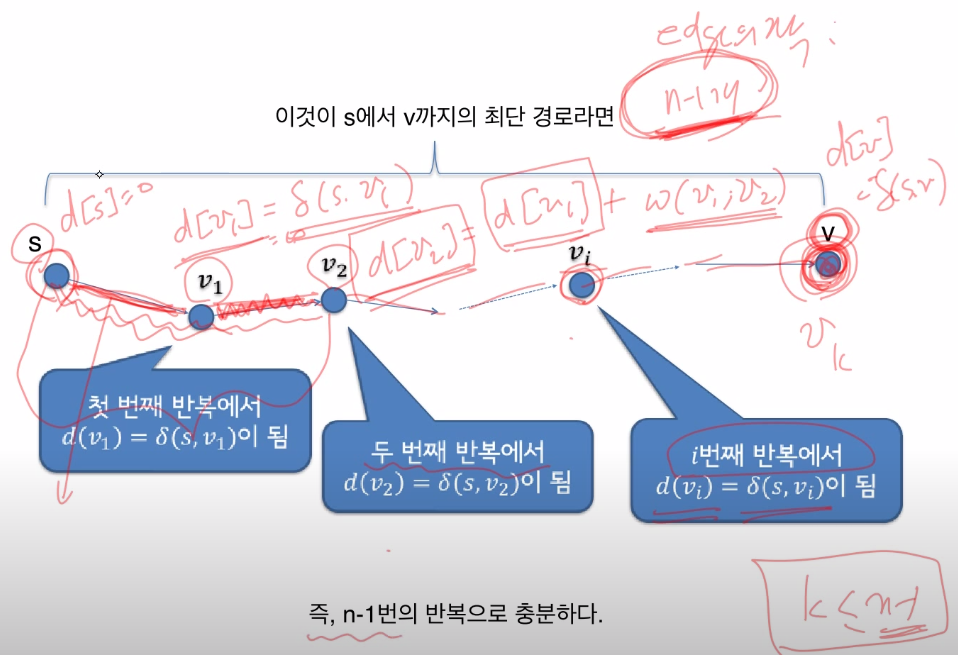
  • Round(1)에서 가장 최단 경로인 $v1$을 구성
  • Round(2)에서 가장 최단 경로인 $v2$를 구성
    $d[v2] = d[v1] + w(v1,v2)$를 만족하니 $v2 = s->v1 + v1->v2$와 같음
  • 최종 $n-1$번 반복 시 $d[v] = d[vi] + w(vi + vi)$
    결국 최악의 경우 $n-1$번의 Round를 반복한다면 모든 노드를 연결하는 최단 경로를 구성할 수 있다.
• 이 알고리즘의 반복으로 구현된 알고리즘이 Bellman Ford 알고리즘이다.

Bellman Ford 알고리즘

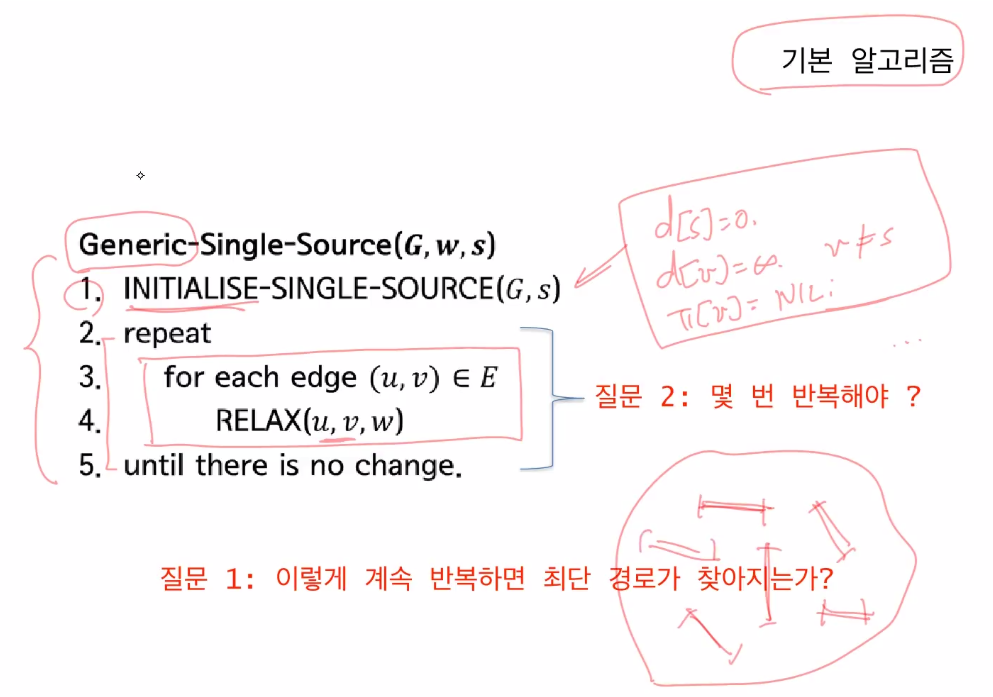
• 벨만 포드 알고리즘은 Realaxation 연산의 반복으로 구성된다
• 사진의 Pesudo 코드에서는 for(int i = 1; i < n -1; i++) 연산까지가
  벨만 포드 알고리즘이고 밑은 음수 사이클의 체크 연산
• $n-1$개의 에지까지 모든 노드에 대해 연산해야하니 $O(nm)$의 시간복잡도를 가진다.

문제점

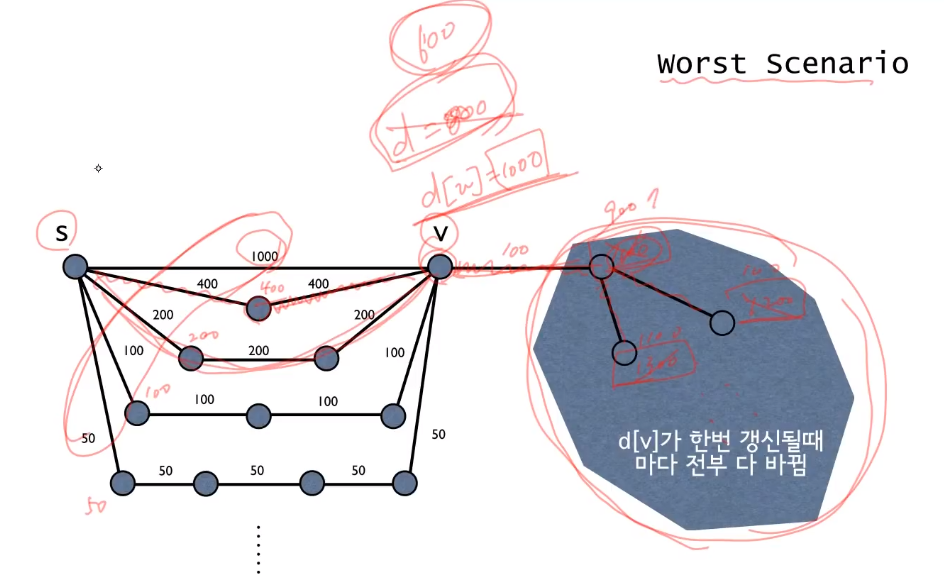
• 최단 경로는 추정치를 갱신시켜 이루어지는데 이는 $v$까지의 최단 경로에 따라 매번 Realaxation 연산이 이루어져야한다는 뜻이다
• $d[v]$가 1000일 때 Realaxation, $d[v]$가 800일 때 Realaxation... 이렇게 매번 갱신이 이루어지는 것보다 $d[v]$가 250일 때 한번만 Realaxation 연산이 이루어지는 것이 낫다.

그래서 이런 벨만포드 알고리즘의 갱신을 개선하여 다익스트라 알고리즘이 탄생했다.

다익스트라 알고리즘은 여기로

참고

영문 위키
권오흠 알고리즘