다익스트라 알고리즘 (with Javascript)

다익스트라 알고리즘이란?

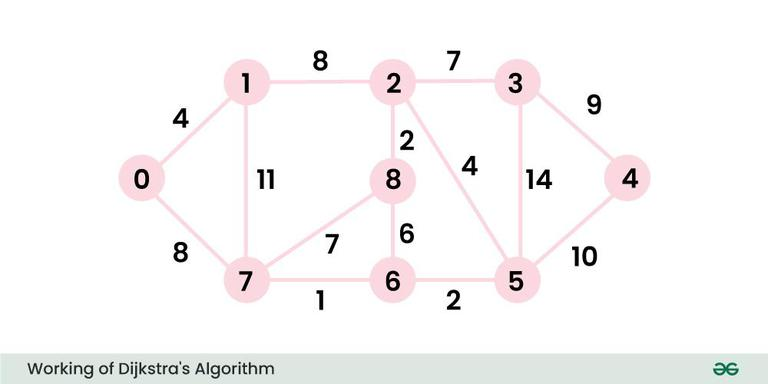
다익스트라 알고리즘이란 그래프에서 최단 경로를 찾기 위한 알고리즘의 한 유형이다.
간선에 비용(가중치)이 있는 그래프에서 한 지점부터 다른 특정 지점까지의 최단 경로를 찾아내는 데에 사용할 수 있다.
단, 음의 간선이 없을 경우에만 정상적으로 동작한다. 음의 간선이란 간선의 비용이 음수(-)인 간선을 말한다.
또한 다익스트라 알고리즘은 매번 '가장 비용이 적은 경로'를 선택하는 과정을 반복하기 때문에 그리디 알고리즘으로 분류된다.

다익스트라 알고리즘을 구현하는 방법은 크게 두 가지가 있다.

1. 구현은 간단하지만 속도는 느린 방식
2. 구현은 더 복잡하지만 속도는 빠른 방식

노드의 개수: V, 간선의 개수: E 일때,
1번은 $O(V^2)$ 의 시간이 걸리고
2번은 $O(E \log V)$ 의 시간이 걸린다.

동작 방식

1. 출발 노드를 설정한다.
2. 최단 거리 테이블을 초기화 한다.
3. 방문하지 않았고 최단 거리가 가장 짧은 노드를 선택한다.
4. 인접한 노드로 갔을 때의 비용을 계산하여 현재 최단 거리 테이블에 저장되어 있는 값보다 현재 노드를 거쳐 갔을 때의 비용이 더 적게 든다면 최단 거리 테이블을 갱신한다.
5. 3번과 4번 과정을 반복한다.

더 자세한 설명을 위해 아래와 같은 그래프가 있다고 가정해보자.

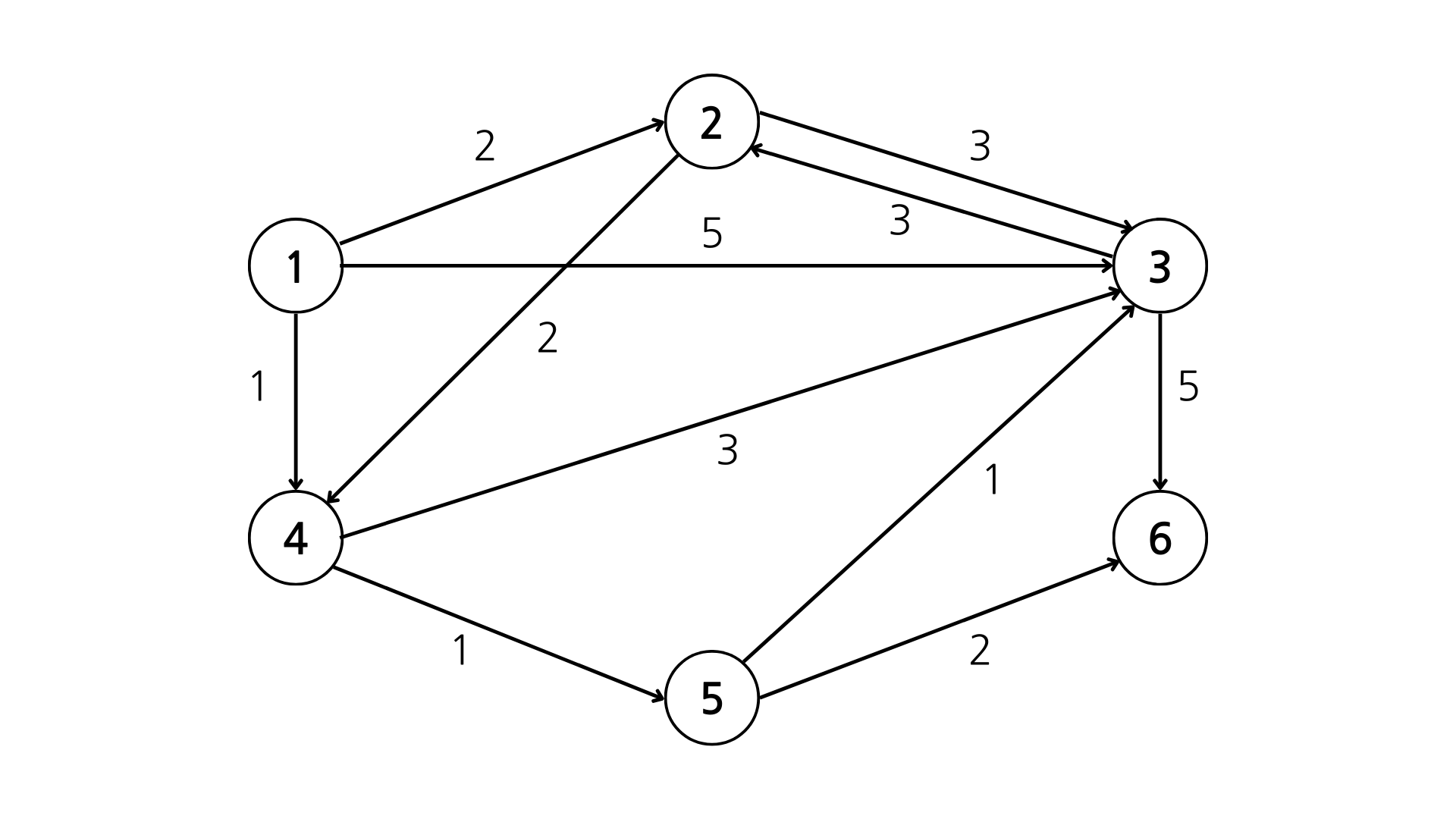
위 그래프를 코드로 나타내면 아래와 같다.

// [노드 번호, 간선 비용]
const graph = [
  	[],							// 0
	[[2,2], [3,3], [4,1]],		// 1
  	[[3,3], [4,2]],				// 2
  	[[2,3], [6,5]],				// 3
  	[[3,3], [5,1]],				// 4
  	[[3,1], [6,2]],				// 5
  	[]							// 6
];

이제 출발 노드를 1번이라고 가정한 뒤 1번 부터 모든 노드로 가는 최단 거리를 구할 것이다.
그러기 위해 최단 거리 테이블을 초기화 한다.
시작 노드부터 시작 노드까지의 거리는 0으로 설정하고 아직 방문하지 않은 노드의 거리는 무한(Infinity, INF)로 초기화한다.

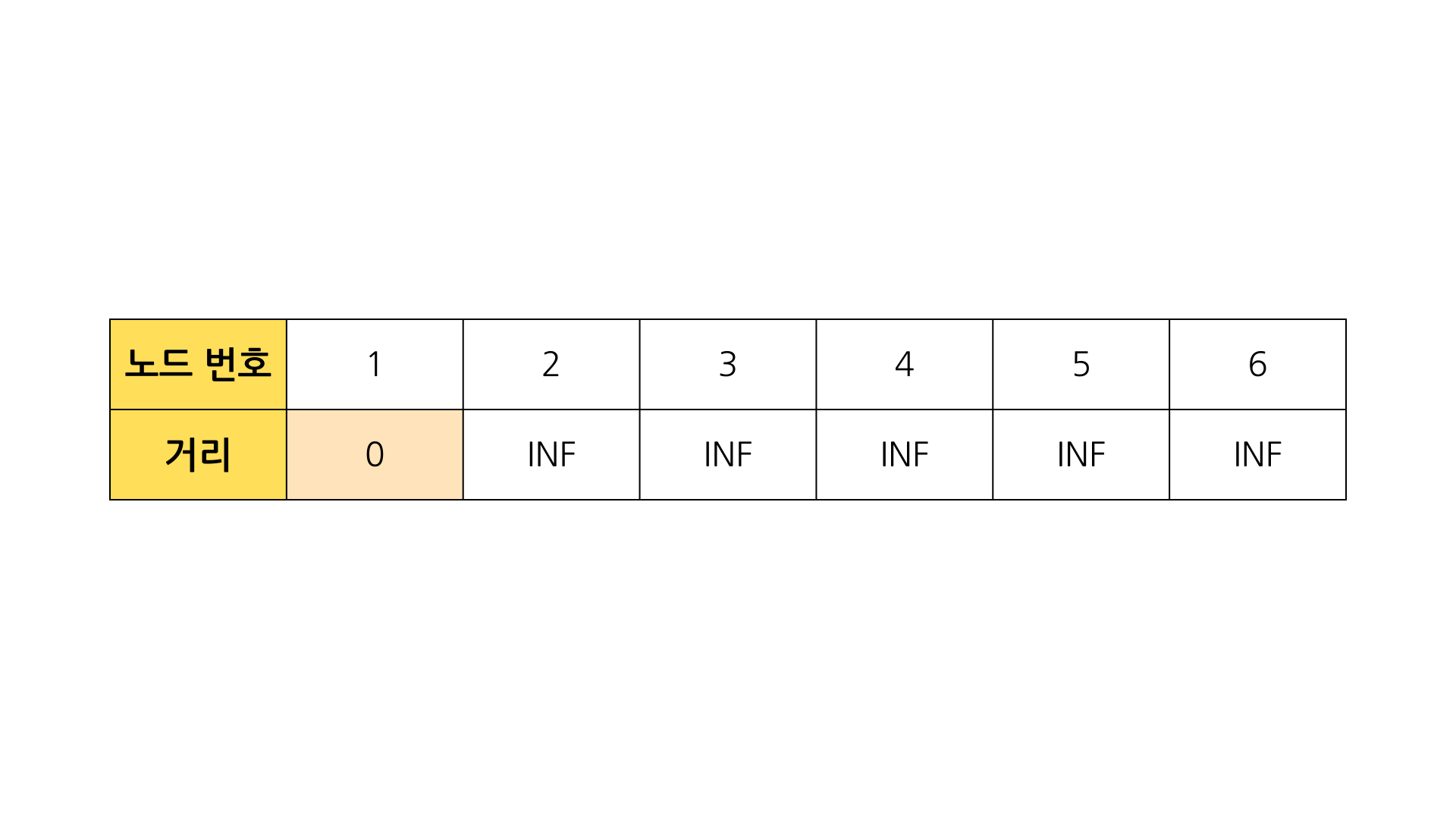
const INF = Infinity
const N = 6 // 노드의 개수
const distance = Array(N+1).fill(INF) // 노드 번호와 인덱스와 일치시키기 위해 N+1개의 배열을 생성
const start = 1; // 시작 노드
distance[start] = 0;

방문하지 않은 노드중 최단 거리가 가장 짧은 노드를 선택하여 방문한다. (1번 노드)
선택한 노드를 거쳐 다른 노드로 갔을 때의 비용을 계산하여 해당 노드를 거쳐갔을 때의 비용이 더 적다면 최단 거리 테이블을 갱신한다.

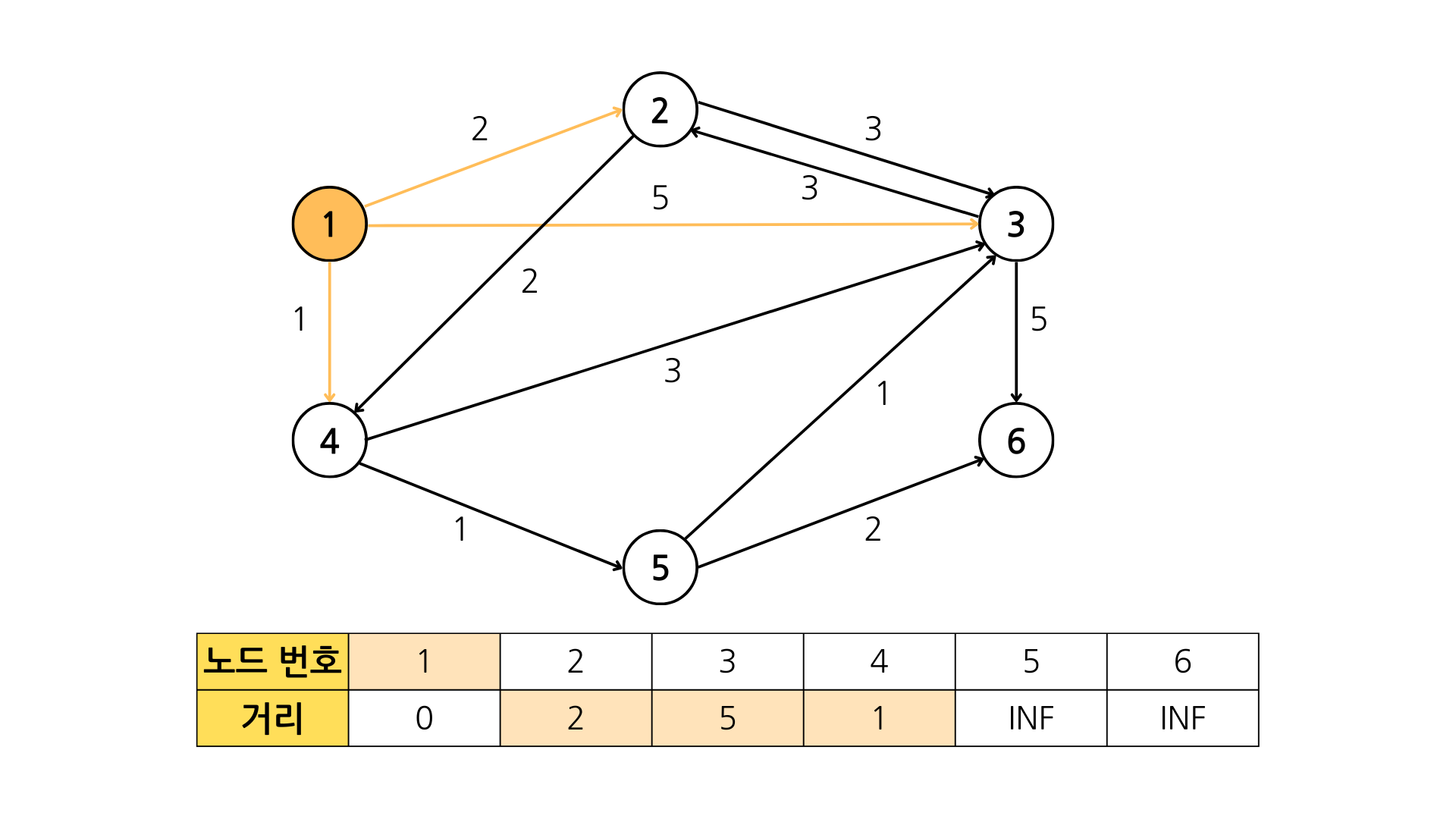
0+2 < INF (true)		// 1번 -> 2번 
0+5 < INF (true) 		// 1번 -> 3번	
0+1 < INF (true) 		// 1번 -> 4번	

또다시 방문하지 않은 노드 중 거리가 가장 짧은 노드를 선택하여 방문하고, 최단 거리 테이블을 갱신하는 과정을 반복한다.

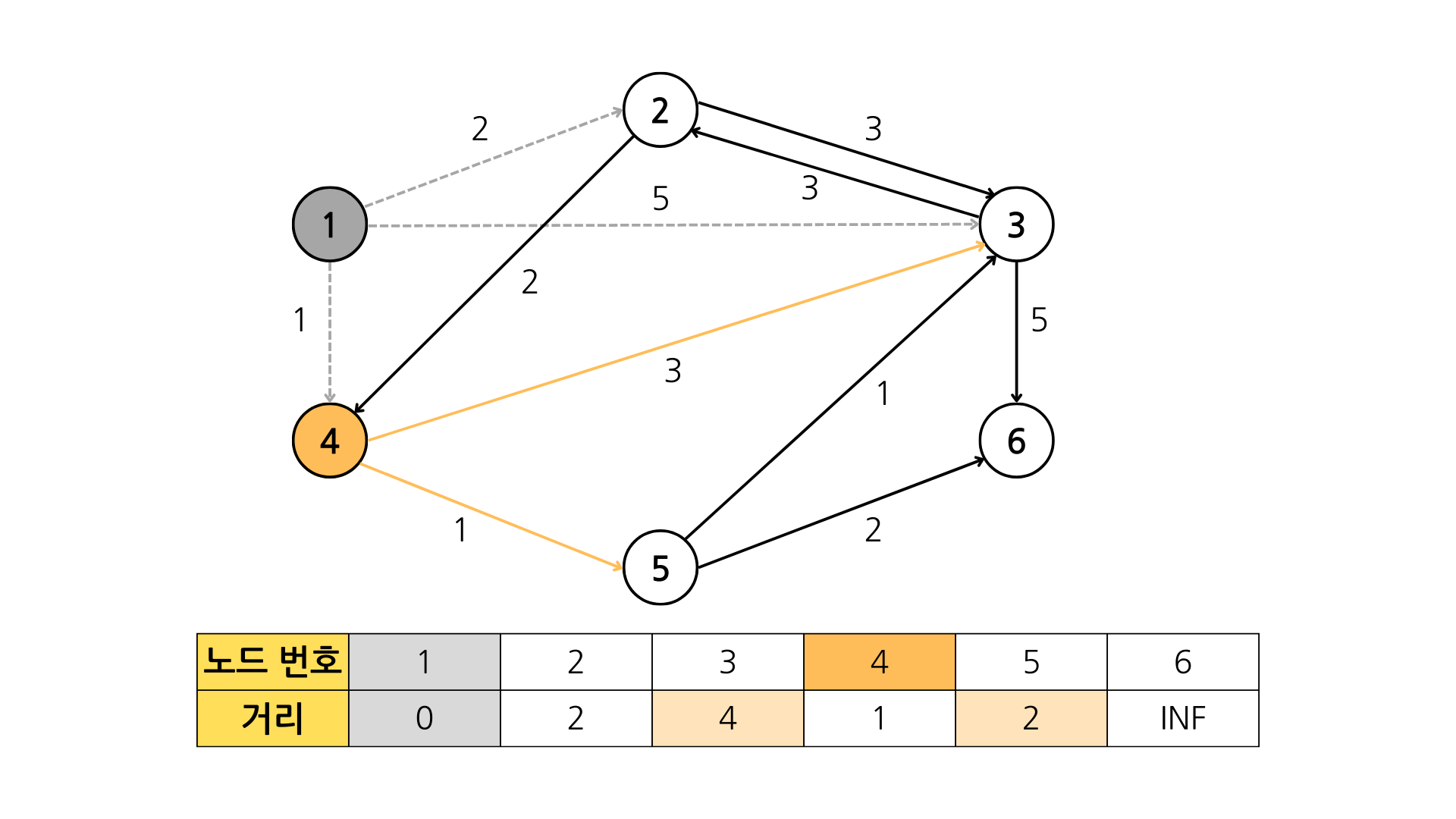
1+3 < 5		(true)		// 4번 -> 3번 
1+1 < INF	(true)		// 4번 -> 5번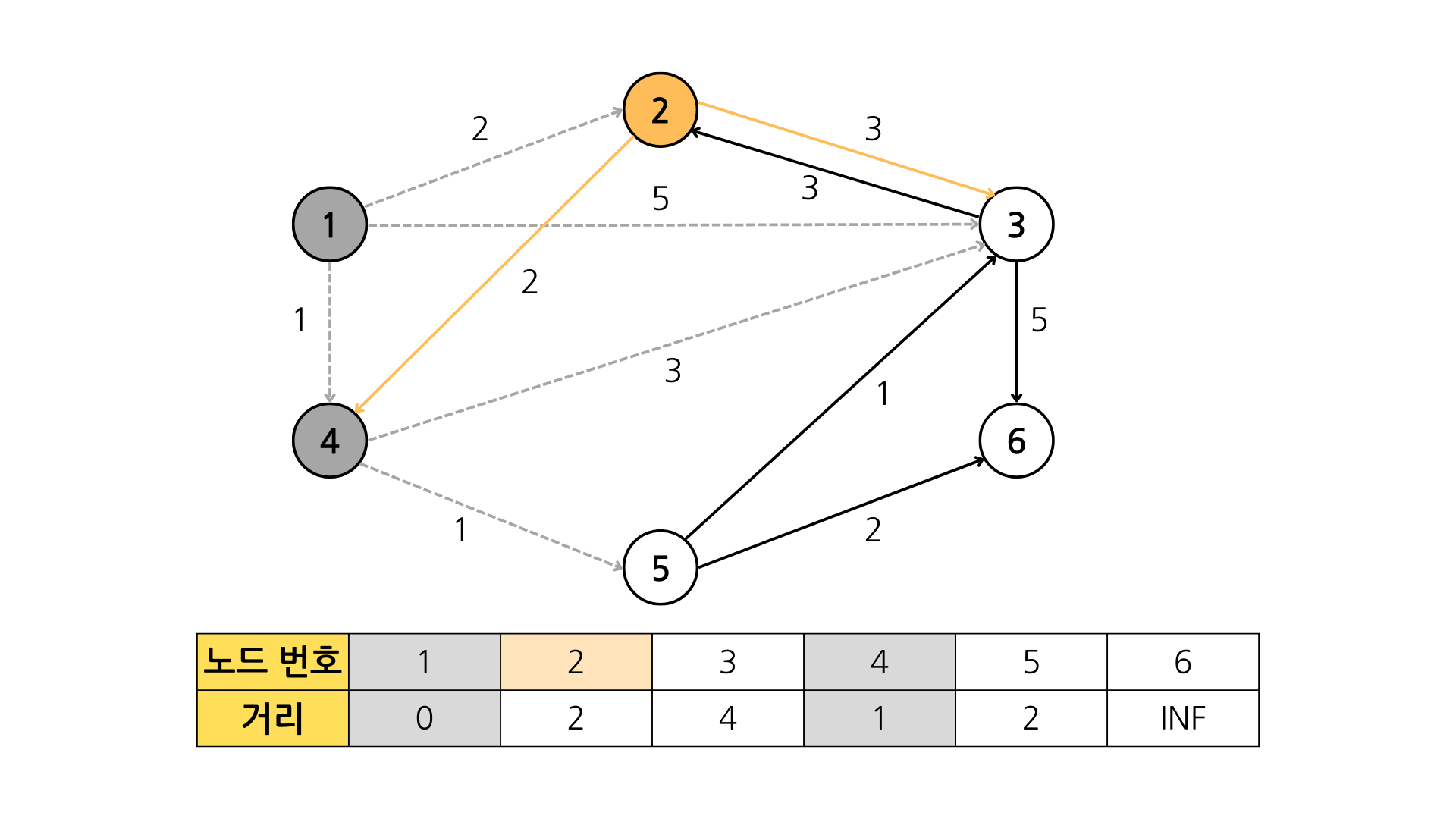

(거리가 가장 짧은 노드가 2개 이상일 경우 번호가 작은 노드부터 방문한다.)

이미 방문한 노드			// 2번 -> 4번 
2+3 < 4	(false)			// 2번 -> 3번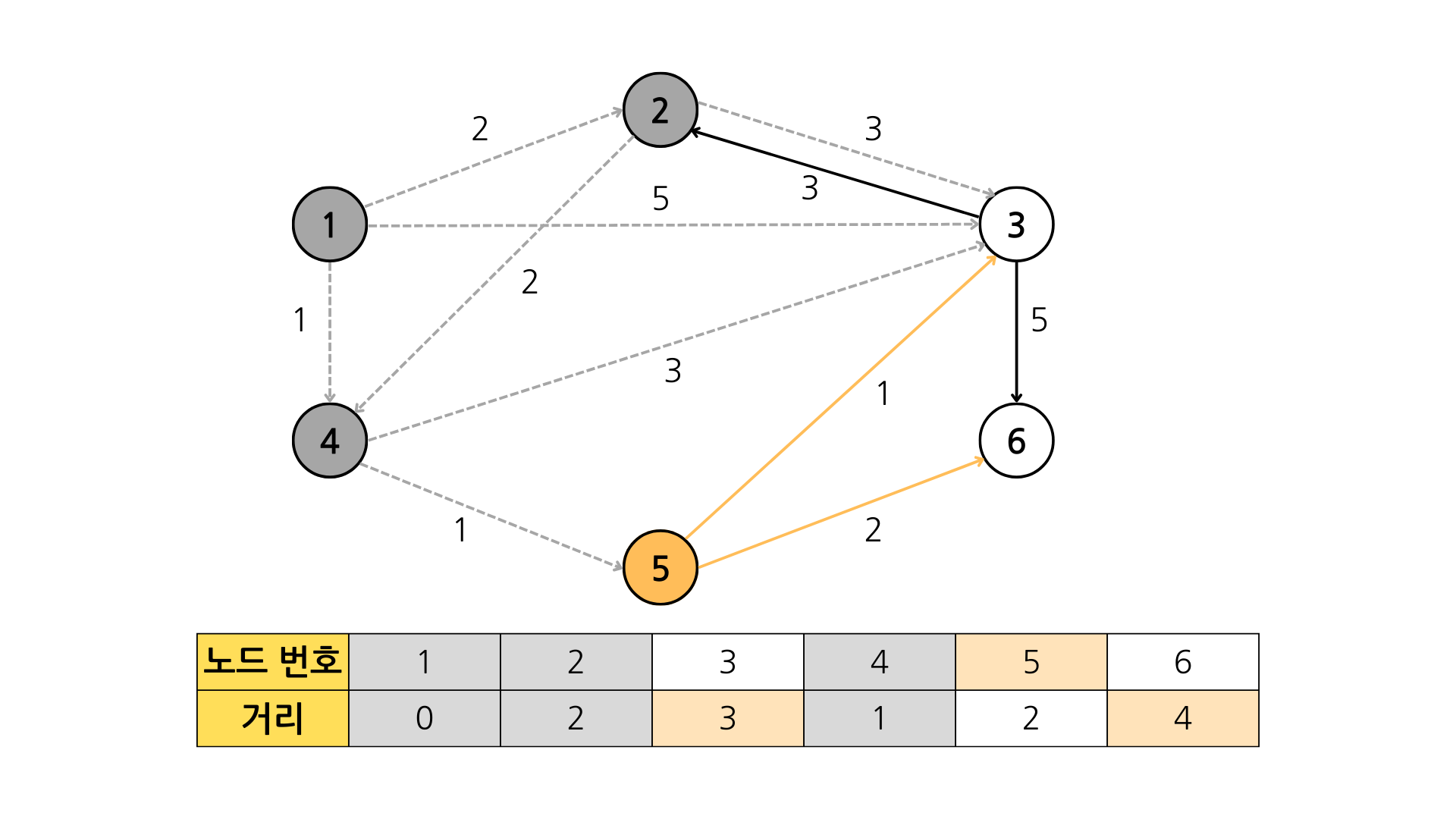

2+1 < 4 	(true)			// 5번 -> 3번 
2+2 < INF	(true)			// 5번 -> 6번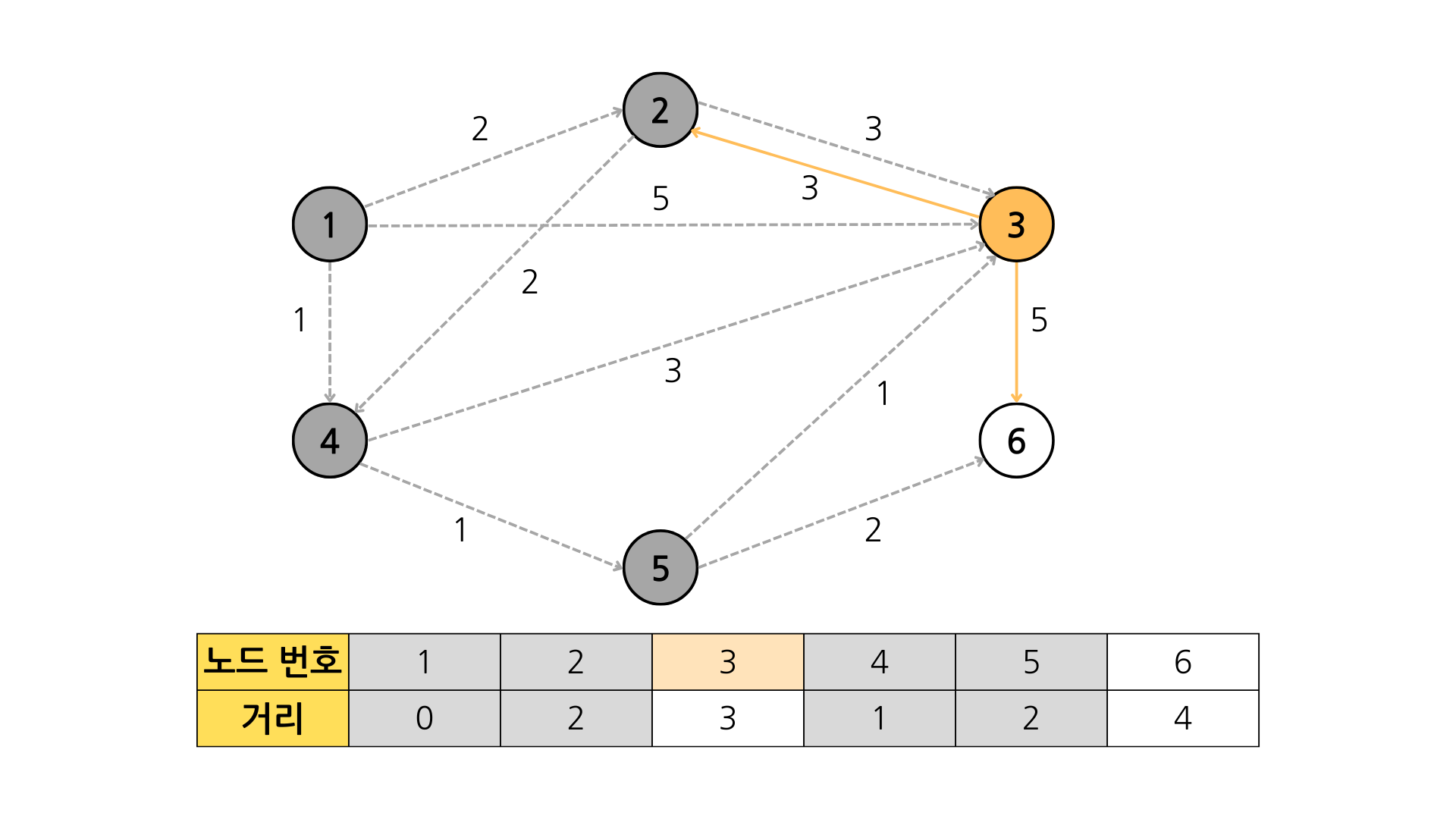

이미 방문한 노드				// 3번 -> 2번 
3+5 < 4	(false)				// 3번 -> 6번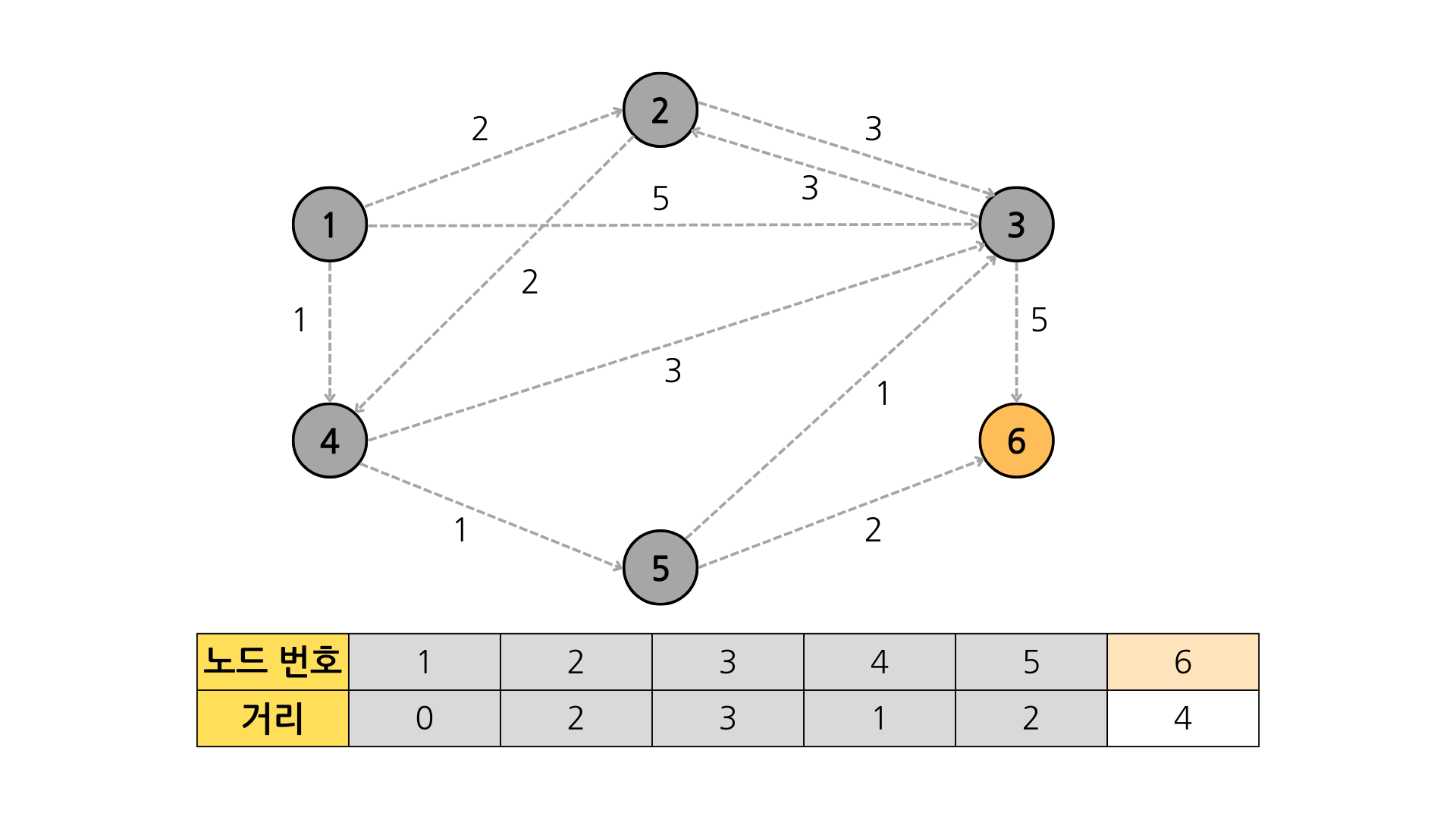

방문할 노드가 없음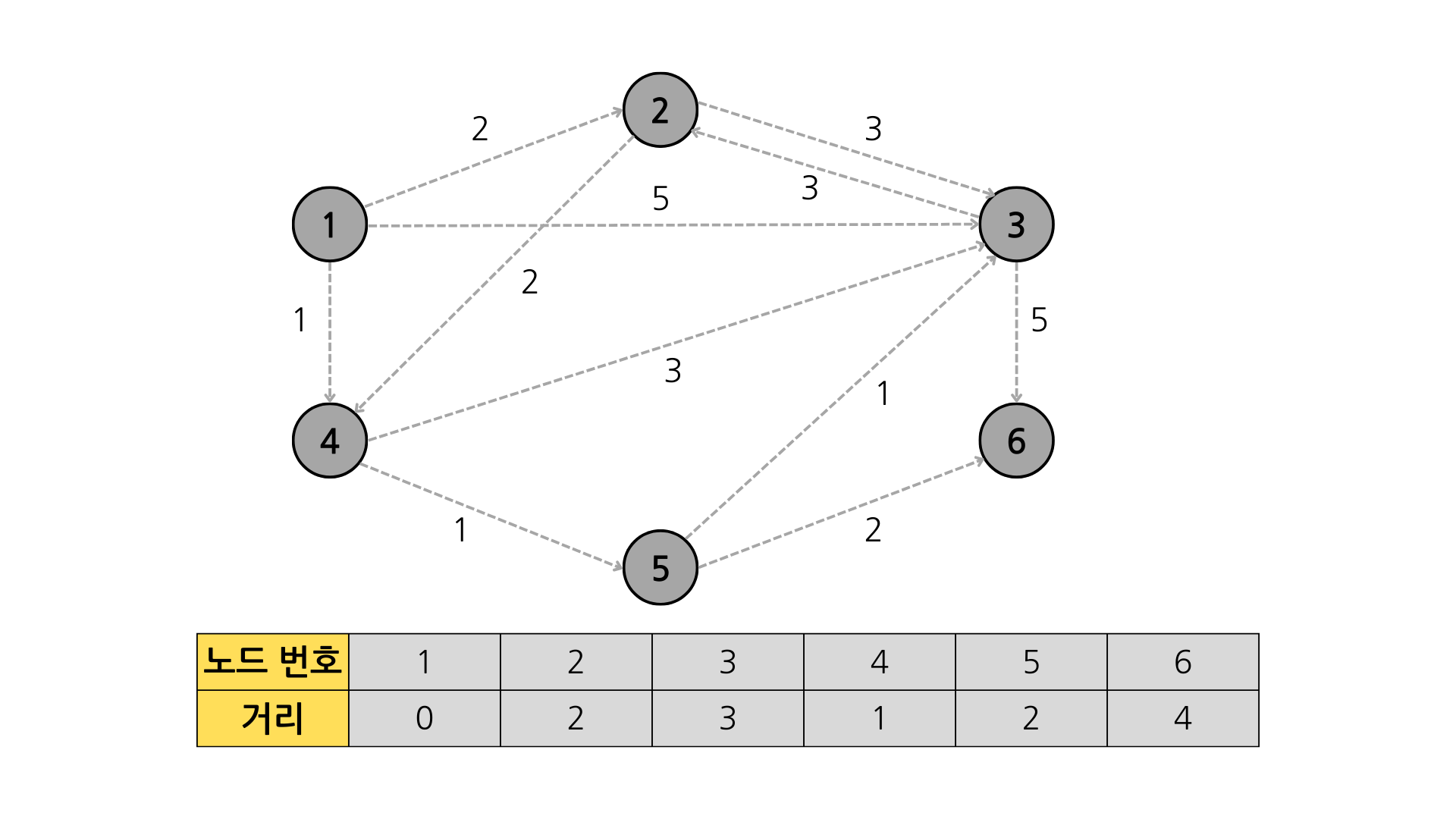

완료

이제 이 과정을 코드로 구현해보면 아래와 같다.

구현 (우선순위 큐 사용 X)

const [n, m] = [6, 11];
const start = 1;
const graph = Array.from({ length: n + 1 }, () => []);
const input = [
    [1, 2, 2],
    [1, 3, 5],
    [1, 4, 1],
    [2, 3, 3],
    [2, 4, 2],
    [3, 2, 3],
    [3, 6, 5],
    [4, 3, 3],
    [4, 5, 1],
    [5, 3, 1],
    [5, 6, 2],
];
input.forEach(([a, b, c]) => graph[a].push([b, c]));
const INF = Infinity;
const visited = Array(n + 1).fill(false);
const distance = Array(n + 1).fill(INF);

// 다익스트라 알고리즘 수행
dijkstra(start);

// 최단거리 테이블 출력
for (let i = 1; i <= n; i++) {
    if (distance[i] === INF) console.log('INFINITY');
    else console.log(distance[i]);
}

// 최단 거리 노드 선택
function getMinIndex() {
    let minValue = INF;
    let index = 0;
    for (let i = 1; i <= n; i++) {
        if (minValue > distance[i] && !visited[i]) {
            minValue = distance[i];
            index = i;
        }
    }
    return index;
}

function dijkstra(start) {
    distance[start] = 0; // 시작 노드의 최단거리 갱신
    visited[start] = true;
    // 시작 노드와 인접한 노드의 최단거리 갱신
    for (let [adj, cost] of graph[start]) {
        distance[adj] = cost;
    }
    // 시작 노드에 대한 작업은 이미 수행해주었기 때문에 n-1회만 실행함
    for (let i = 0; i < n - 1; i++) {
        let cur = getMinIndex();
        visited[cur] = true;
        for (let [adj, cost] of graph[cur]) {
            let totalCost = distance[cur] + cost;
            if (distance[adj] > totalCost) distance[adj] = totalCost;
        }
    }
}

이 방식은 매번 반복할 때마다 최단 거리가 가장 짧은 노드를 찾기 위해 getMinIndex() 함수를 실행시켜서 모든 노드를 선형적으로 탐색하기 때문에 위에서 말한대로 $O(V^2)$ 의 시간복잡도를 갖는다. 따라서 노드의 개수가 10000개만 넘어가도 시간 초과가 난다.

이를 해결하기 위해 최소힙을 기반으로 한 우선순위 큐(Priority Queue)를 이용하여 동작 속도를 개선시킬 수 있다.
우선순위 큐를 사용하면 큐에 데이터를 삽입, 삭제할 때마다 $O(\log E)$ 의 시간이 소요되고, 삽입과 삭제를 간선의 개수만큼 반복하므로 시간 복잡도는 $O(E\log E)$ 가 된다.

또한 중복 간선을 포함하지 않을 경우, 모든 노드를 간선으로 연결했을 때 간선의 개수는 $\frac{v \times (v-1)}{2}$ 이므로 E는 항상 V$^2$ 보다 작다. 다시 말해 $\log E$는 $\log V^2$보다 작다. 이때 $O(\log V^2)$ 은 $O(2\log V)$ 이고, 이는 또다시 빅오 표기법에 의해 상수항이 소거되어 $O(logV)$ 가 된다. 따라서 다익스트라 알고리즘의 시간복잡도 $O(E\log E)$ 는 $O(E \log V)$ 로 표기할 수 있다.

아래는 우선순위 큐를 이용해 구현한 다익스트라 알고리즘이다.

구현 (우선순위 큐 사용 O)

class PriorityQueue {
    constructor() {
        this.heap = [];
    }

    enqueue(node, dist) {
        this.heap.push({ node, dist });
        this.heapifyUp(this.heap.length - 1);
    }

    heapifyUp(index) {
        while (index > 0) {
            const parentIndex = (index - 1) >> 1;
            if (this.heap[parentIndex].dist <= this.heap[index].dist) break;
            [this.heap[parentIndex], this.heap[index]] = [this.heap[index], this.heap[parentIndex]];
            index = parentIndex;
        }
    }

    dequeue() {
        const min = this.heap[0];
        const end = this.heap.pop();
        if (this.heap.length > 0) {
            this.heap[0] = end;
            this.heapifyDown(0);
        }
        return min;
    }

    heapifyDown(index) {
        while (index < this.heap.length) {
            const left = (index << 1) + 1;
            const right = (index << 1) + 2;
            let smallest = index;
            if (this.heap[left] && this.heap[left].dist < this.heap[smallest].dist) {
                smallest = left;
            }
            if (this.heap[right] && this.heap[right].dist < this.heap[smallest].dist) {
                smallest = right;
            }
            if (smallest === index) break;
            [this.heap[index], this.heap[smallest]] = [this.heap[smallest], this.heap[index]];
            index = smallest;
        }
    }

    isEmpty() {
        return this.heap.length === 0;
    }
}

const [n, m] = [6, 11];
const start = 1;
const graph = Array.from({ length: n + 1 }, () => []);
const input = [
    [1, 2, 2],
    [1, 3, 5],
    [1, 4, 1],
    [2, 3, 3],
    [2, 4, 2],
    [3, 2, 3],
    [3, 6, 5],
    [4, 3, 3],
    [4, 5, 1],
    [5, 3, 1],
    [5, 6, 2],
];
input.forEach(([s, e, cost]) => graph[s].push([e, cost]));
const INF = Infinity;
const distance = Array(n + 1).fill(INF);

// 다익스트라 알고리즘 수행
dijkstra(start);

// 결과 출력
for (let i = 1; i <= n; i++) {
    if (distance[i] === INF) console.log('INFINITY');
    else console.log(distance[i]);
}

function dijkstra(start) {
    const pq = new PriorityQueue();
    pq.enqueue(start, 0); // 시작 노드, 거리
    distance[start] = 0; // 시작 노드부터 시작노드까지의 거리
    while (!pq.isEmpty()) {
        let { node, dist } = pq.dequeue();
        // 해당 노드를 이미 처리한 적이 있다면 무시
        if (distance[node] < dist) continue;
        for (let [adj, cost] of graph[node]) {
            let totalCost = distance[node] + cost;
            if (distance[adj] > totalCost) {
                distance[adj] = totalCost;
                pq.enqueue(adj, totalCost);
            }
        }
    }
}

최소힙과 우선순위 큐에 관련된 설명은 전에 포스팅한 글에 설명해놓았다.

참고

• 이것이 코딩테스트다 (with 파이썬)