문제
코드 (BFS)
const filePath = process.platform === 'linux' ? '/dev/stdin' : './Javascript/input.txt';
const [N, K] = require('fs').readFileSync(filePath).toString().trim().split(' ').map(Number);
const visited = Array(10 ** 6).fill(false);
let answer = 0;
const queue = [[N, 0]];
let front = 0;
visited[N] = true;
while (queue.length > front) {
const [cur, sec] = queue[front++];
if (cur === K) {
answer = sec;
break;
}
for (let next of [cur - 1, cur + 1, cur * 2]) {
if (!visited[next] && 0 <= next && next <= 100000) {
visited[next] = true;
queue.push([next, sec + 1]);
}
}
}
console.log(answer);풀이
처음엔 그래프 탐색을 사용해서 풀면 시간 초과가 날줄 알았다. 매 숫자마다 -1, +1, *2 이렇게 세 번의 연산을 수행해주어야 하기 때문이다.
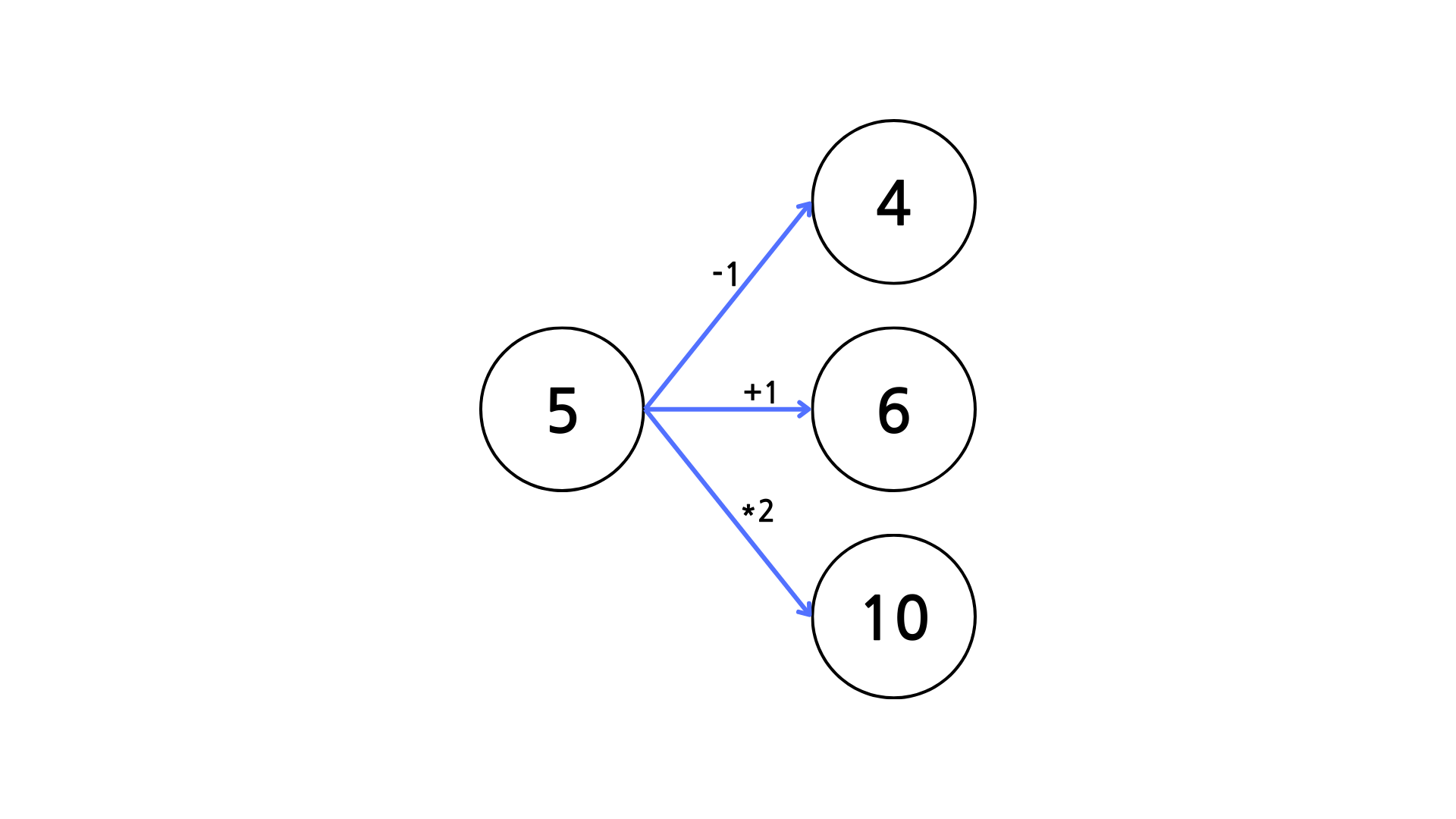
이럴경우 수가 조금만 커져도 아래 이미지처럼 연산 횟수가 기하급수적으로 증가한다.
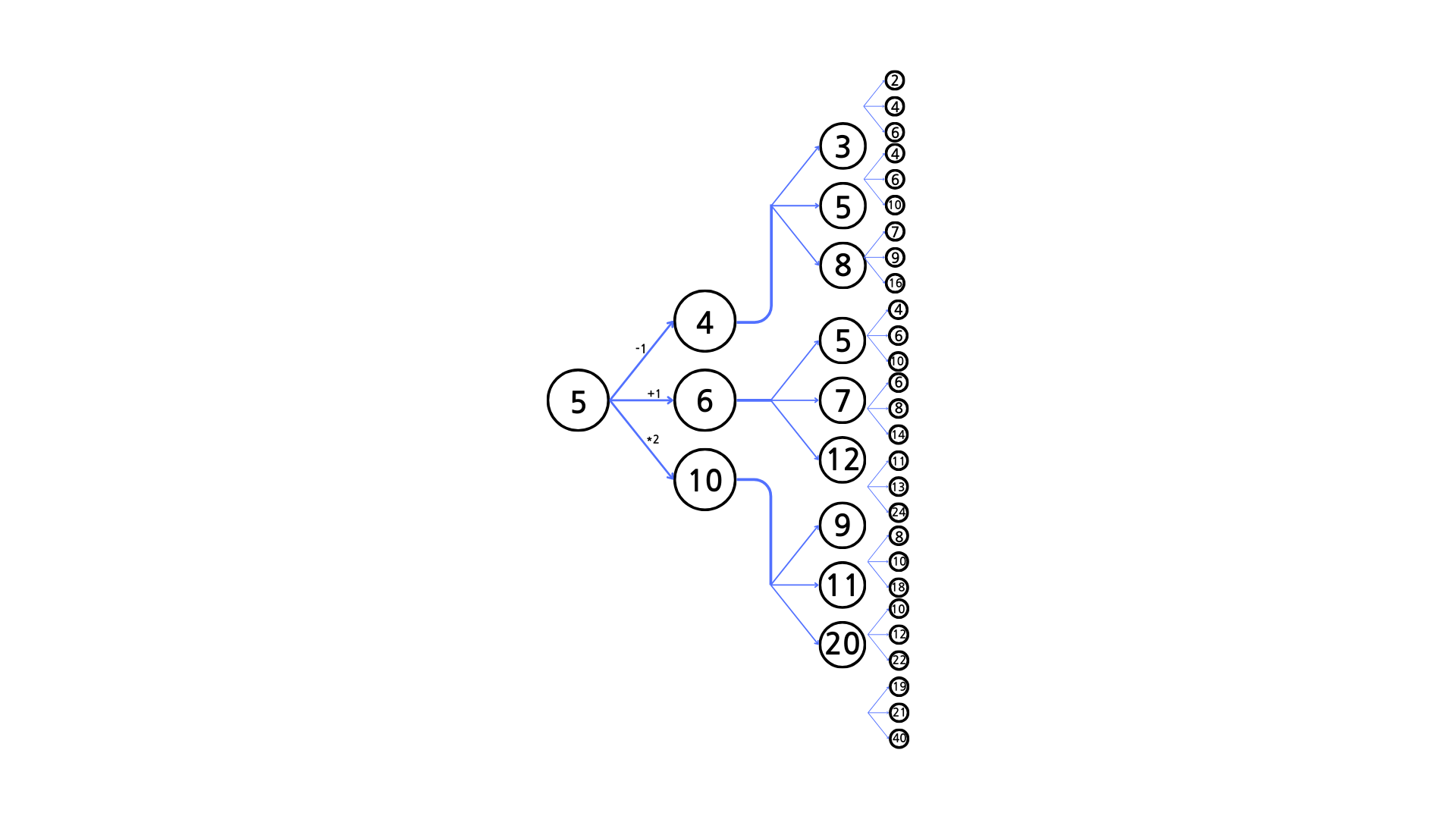
최악의 경우 연산 횟수는 3^100,000이기 때문에 무조건 시간초과가 날 것이다.
하지만 이 중에서는 이미 한번 등장한 적 있는 수가 또다시 등장하는, 다시 말해 중복된 수가 많다.
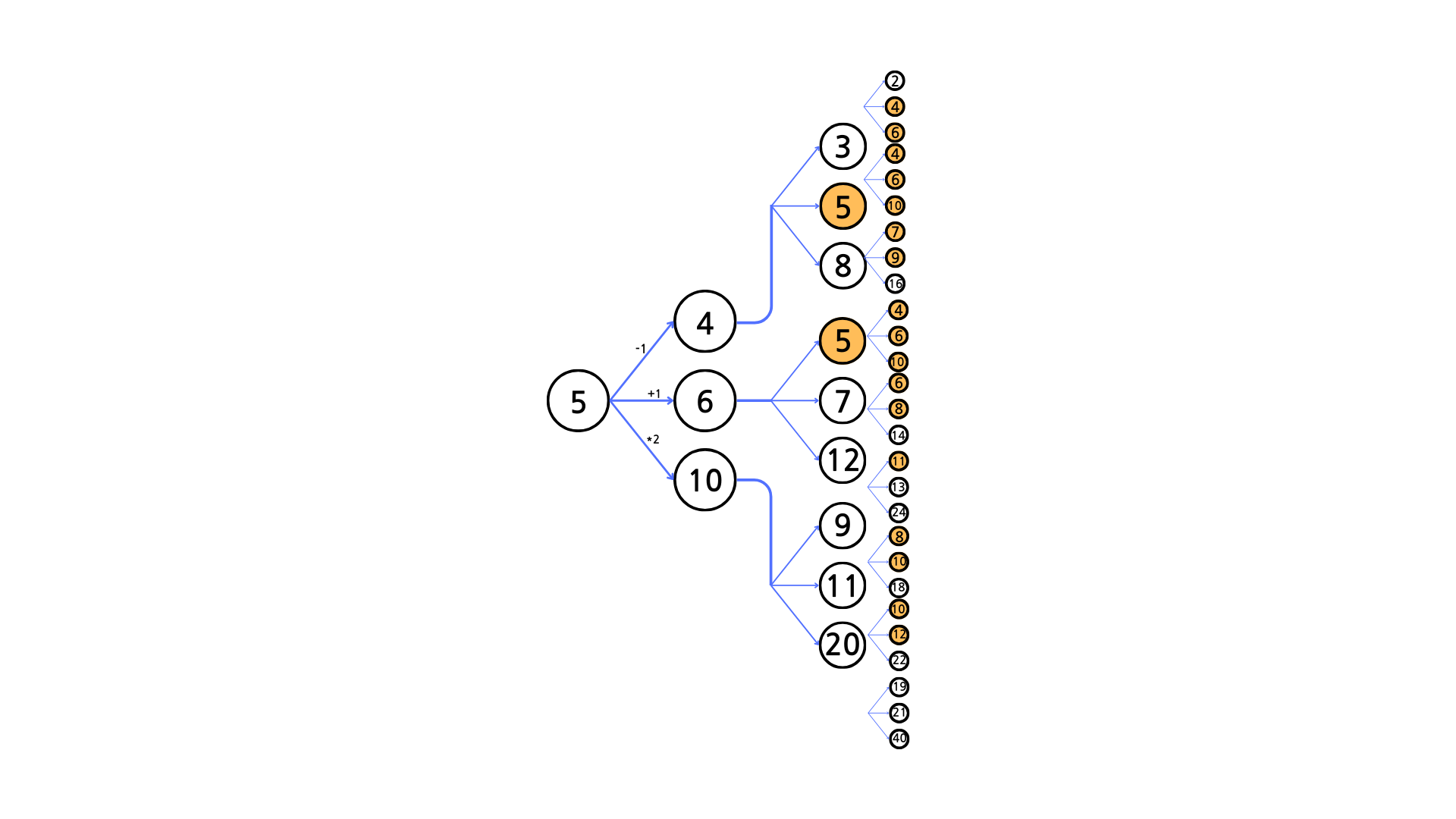
위 그림처럼 1초씩 증가할수록 중복된 수는 더욱 증가할 것이다.
우리는 최단 시간(거리)만 찾으면 되기 때문에 이미 방문한 적 있는 수는 다시 방문하지 않아도 된다. (이미 방문한적 있다면 그 당시가 그 수로 가는 최단 거리이기 때문에)
따라서 이미 방문한 적 있는 번호를 다시 방문하지 않도록 만들어주면 시간 초과를 피할 수 있다.
코드 (DP)
const filePath = process.platform === 'linux' ? '/dev/stdin' : './Javascript/input.txt';
const [N, K] = require('fs').readFileSync(filePath).toString().trim().split(' ').map(Number);
const dp = Array(10 ** 6).fill(Infinity);
// 1번
if (N >= K) {
console.log(N - K);
process.exit(0);
}
// 2번
for (let i = 0; i < N; i++) {
dp[i] = N - i;
}
// 3번
dp[N] = 0;
for (let i = N + 1; i <= K; i++) {
// i/2 에서 온 경우와 i-1에서 온 경우 비교
if (i % 2 === 0) {
dp[i] = Math.min(dp[i >> 1], dp[i - 1]) + 1;
}
// i-1 에서 온 경우와 i+1 에서 온 경우 비교
else {
dp[i] = Math.min(dp[i - 1] + 1, dp[(i + 1) >> 1] + 2);
}
}
console.log(dp[K]);풀이
이 문제는 DP로도 풀 수 있다.
풀이는 아래 블로그를 참고했다.
https://didu-story.tistory.com/441
- 우선 K가 N보다 작을 때는 +1과 *2 연산으로는 K에 도달할 수가 없다. 그 말은 즉, -1연산만 사용해서 가야하기 때문에 K가 N보다 작거나 같을 때는 N-K번의 -1 연산을 수행해서 K지점에 도착할 수 있다. 따라서 아래 조건문을 추가한다.
if (N >= K) {
console.log(N - K);
process.exit(0);
}- N=17, K=32라고 가정해보자. N에서 K까지 가장 빠르게 갈 수 있는 방법은
N-1(16) -> N*2(32)이렇게 두 번에 거쳐 가는 것이 가장 빠르다. 이처럼 N보다 작은 수를 경유해서 가는 경우가 더 빠를 때도 있기 때문에 dp[0~N] 까지를 미리 초기화 시켜놓아야 한다.
for (let i = 0; i < N; i++) {
dp[i] = N - i;
}- i가 짝수인 경우에는
i-1혹은i/2로부터 i 지점에 도착할 수 있다.
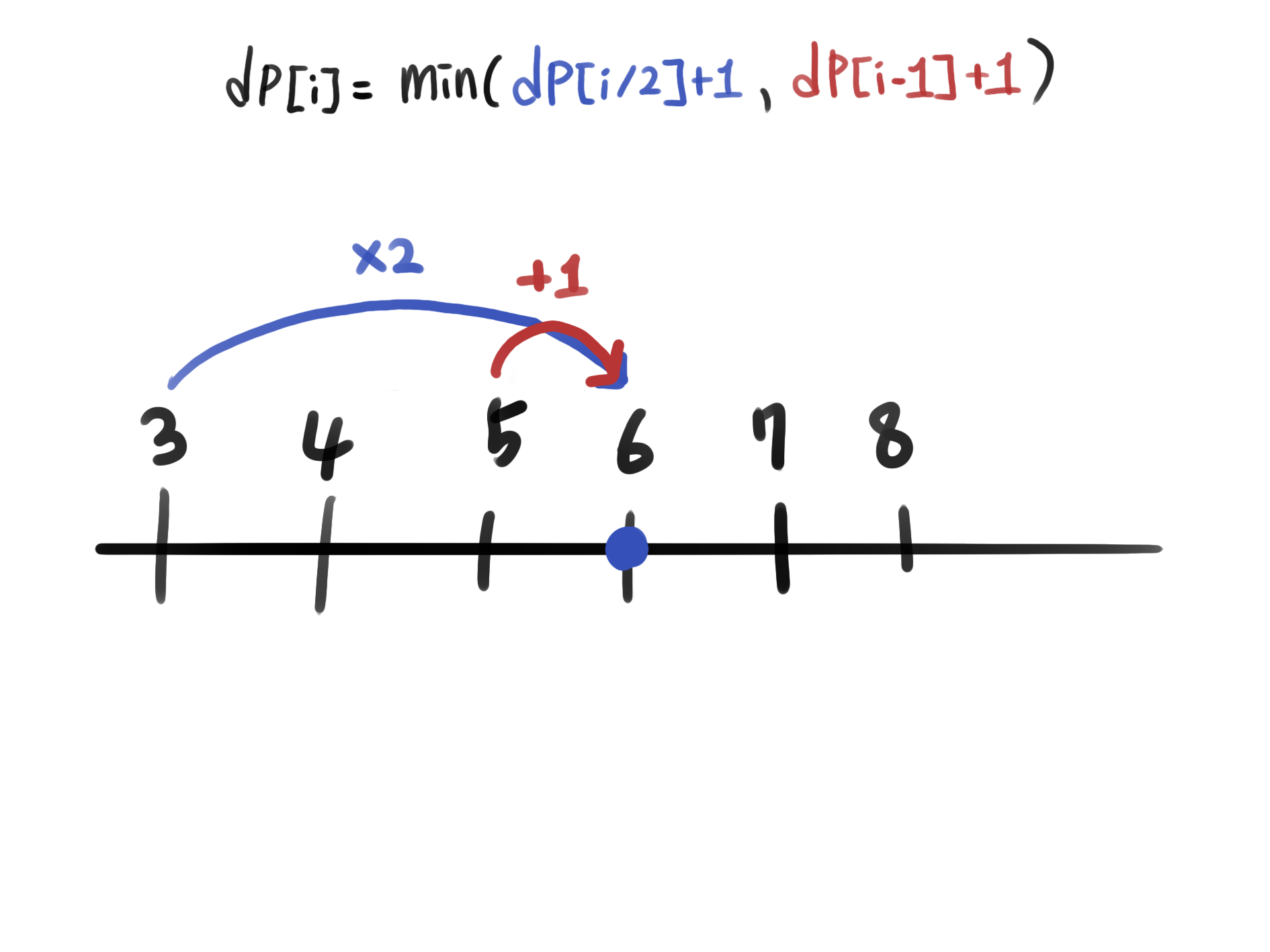
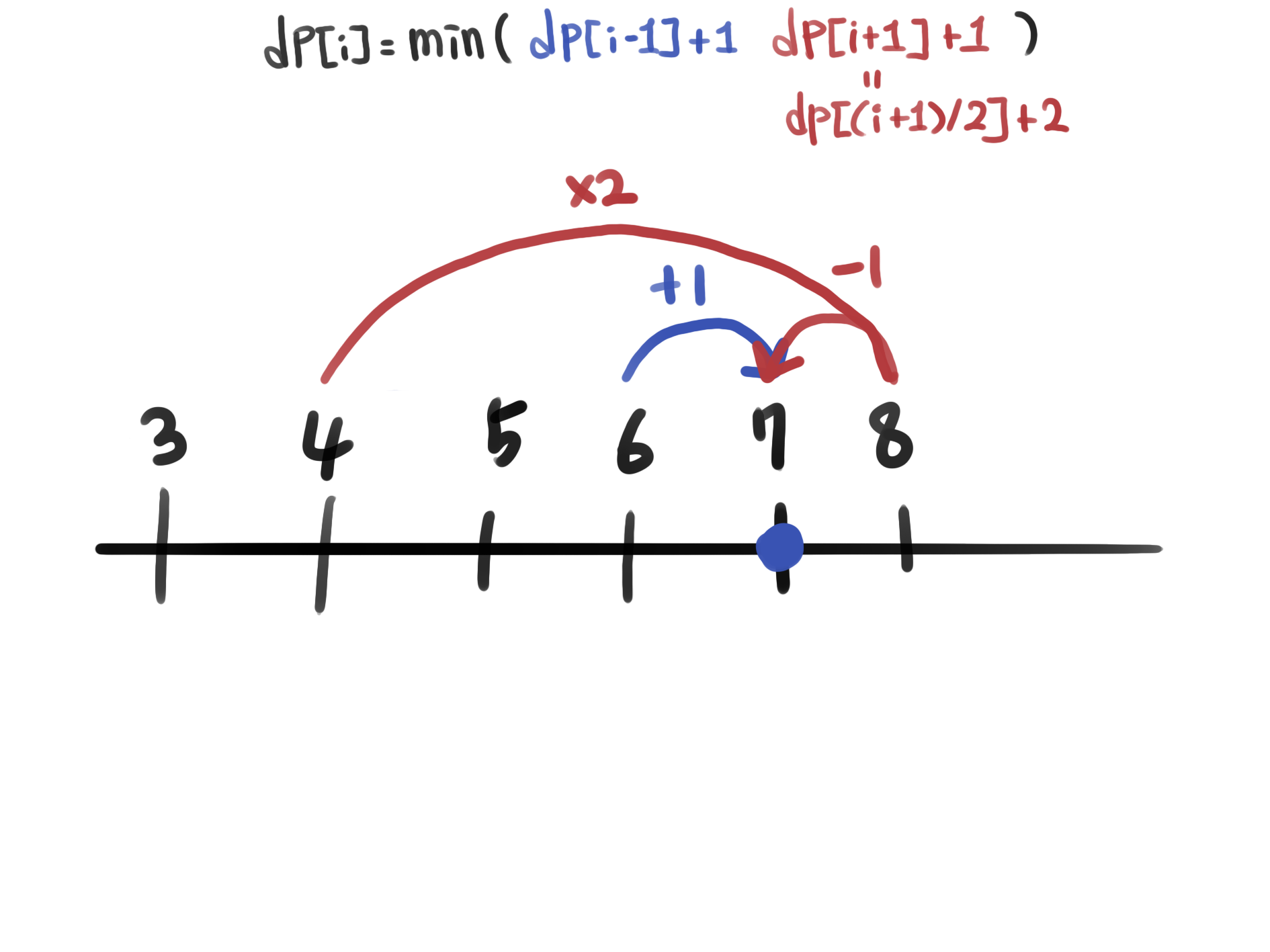
i가 홀수인 경우에는 i-1 혹은 i+1로부터 올 수 있다. 하지만 여기서 주의할 점은 i는 0부터 1씩 증가하며 dp테이블의 값을 갱신해나간다는 것이다. 따라서 i일 때 i+1에 위치에는 처음에 dp테이블을 초기화 할때 넣어줬던 값이 들어가 있을 것이다.
따라서 i+1 지점 대신 (i+1)/2 지점을 참조해준다. 이 때 +1과 /2 연산으로 인해 총 두 단계를 거슬러 올라갔으므로 dp[(i-1)/2]+1 이 아니라 dp[(i-1)/2]+2 로 해준다.
dp[N] = 0;
for (let i = N + 1; i <= K; i++) {
// i/2 에서 온 경우와 i-1에서 온 경우 비교
if (i % 2 === 0) {
dp[i] = Math.min(dp[i >> 1], dp[i - 1]) + 1;
}
// i-1 에서 온 경우와 i+1 에서 온 경우 비교
else {
dp[i] = Math.min(dp[i - 1] + 1, dp[(i + 1) >> 1] + 2);
}
}

