[백준] 2228_구간 나누기 (Javascript)

문제

BOJ2228_구간 나누기

코드

const filePath = process.platform === 'linux' ? '/dev/stdin' : './Javascript/input.txt';
const input = require('fs').readFileSync(filePath).toString().trim().split('\n');
const [N, M] = [0].concat(input[0].split(' ').map(Number));
const arr = input.slice(1).map(Number);
const dp1 = Array.from({ length: N + 1 }, () => [0].concat(Array(M + 1).fill(-Infinity)));
const dp2 = Array.from({ length: N + 1 }, () => [0].concat(Array(M + 1).fill(-Infinity)));

for (let i = 1; i <= N; i++) {
    for (let j = 1; j <= Math.min(M, Math.ceil(i/2)); j++) {
      	// i 번째 원소를 포함하지 않을 경우
        dp1[i][j] = Math.max(dp1[i - 1][j], dp2[i - 1][j]);
      	// i 번째 원소를 포함하는 경우
        dp2[i][j] = Math.max(dp1[i - 1][j - 1], dp2[i - 1][j]) + arr[i];
    }
}
console.log(Math.max(dp1[N][M], dp2[N][M]));

시간 복잡도

이 문제를 브루트 포스로 풀면 시간 복잡도는 $O(2^N)$이 되고, $N\le100$ 이므로 시간초과가 발생한다.
따라서 다른 풀이법으로 풀어야 하는 문제이고, DP를 사용해서 $O(N\times M)$ 의 시간복잡도로 풀 수 있다.

풀이

어려워서 풀이를 보고 푼 문제였다.
이 문제는 2차원 DP테이블 두 개를 사용해서 풀 수 있다.

우선 문제의 조건을 보면 각 구간은 인접해 있으면 안된다고 나와있으므로 점화식은 대충 dp[i] = max(arr[i] + dp[i-2], dp[i-1]) 이런 꼴과 비슷할 것 같은데, 그 다음 조건에 정확히 M개의 구간이 있어야 한다고 나와있다. 따라서 위 점화식을 그대로 사용하면 정확히 M개의 구간을 보장할 수 없으므로 다른 식을 세워야 한다.

나는 아래 블로그를 참고해서 풀었다.

참고 블로그

이 블로그에 나와있는 설명과 내 코드를 토대로 부연 설명만 추가해 보겠다.

우선 dp 테이블이 아래와 같이 생성된다.

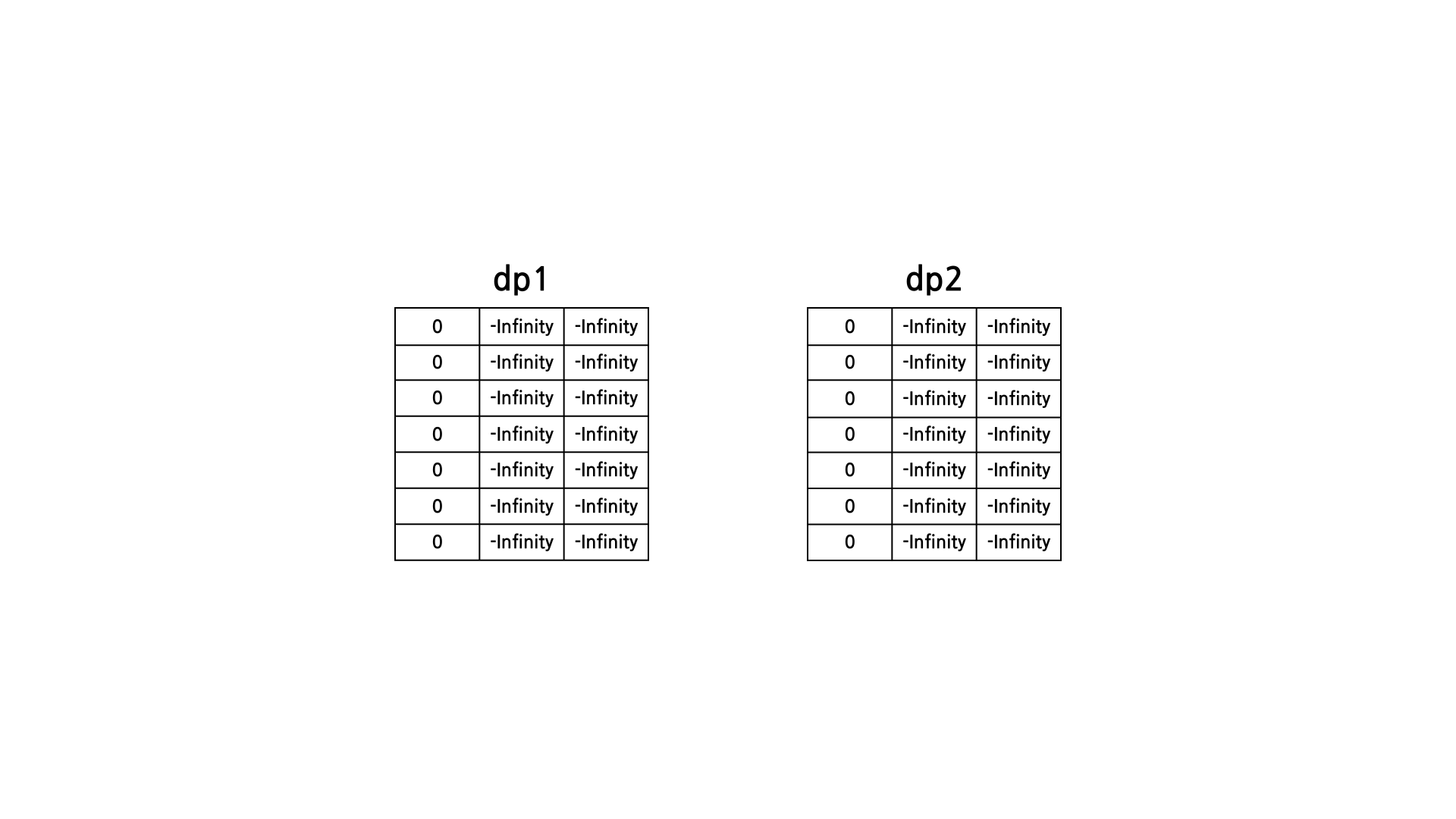
dp1은 i번 째 원소를 포함하지 않는 경우의 최대 구간합이 저장되고, dp2는 i번 째 원소를 포함하지 않는 경우의 최대 구간합이다.

그리고 i가 증가함에 따라 두 dp테이블의 세로축이 움직이고, j(구간의 수)가 증가함에 따라 가로축이 움직인다.

문제의 예시를 기준으로 그림으로 dp 테이블의 변화를 살펴보면 아래와 같다.

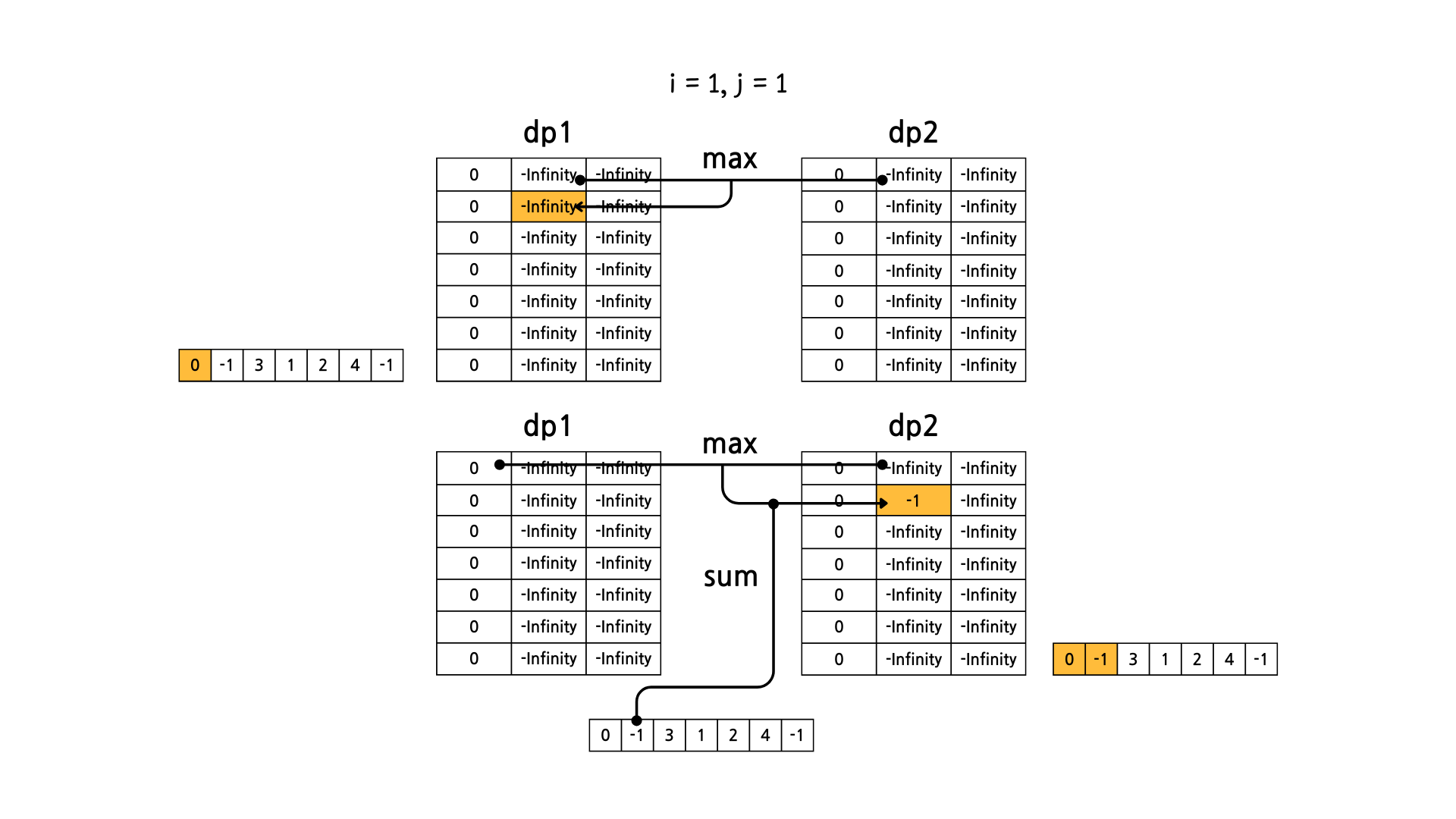
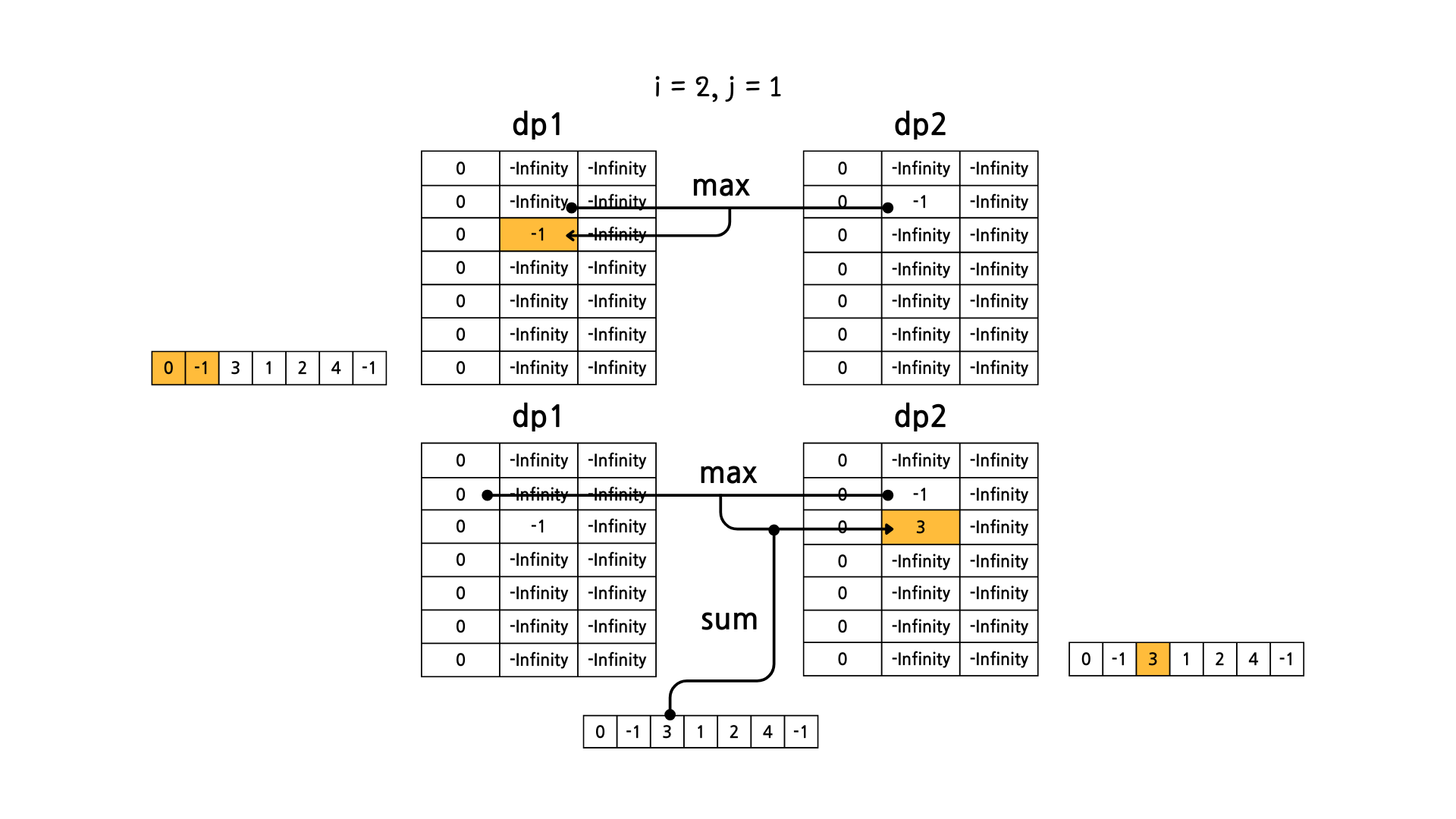
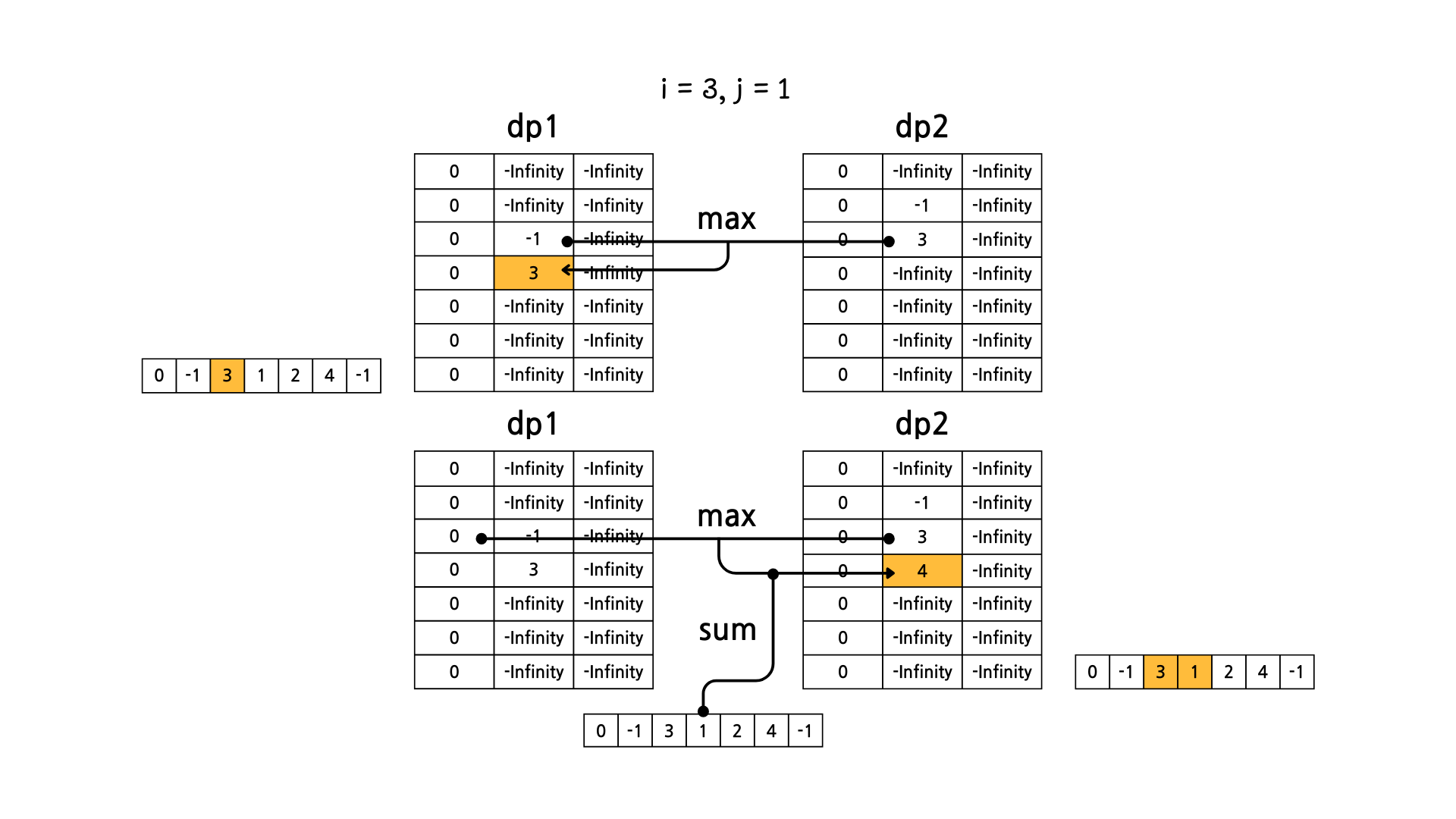
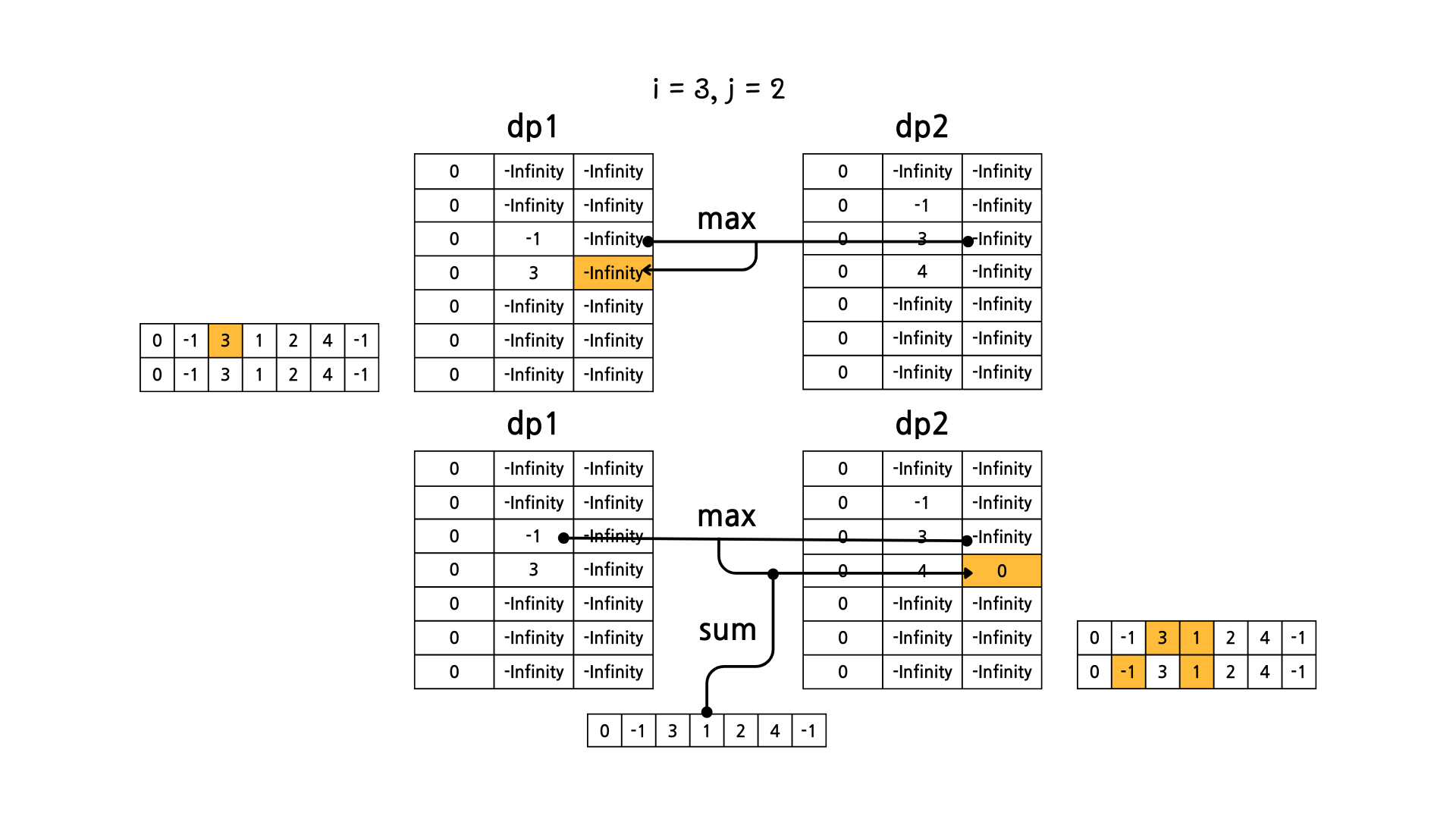
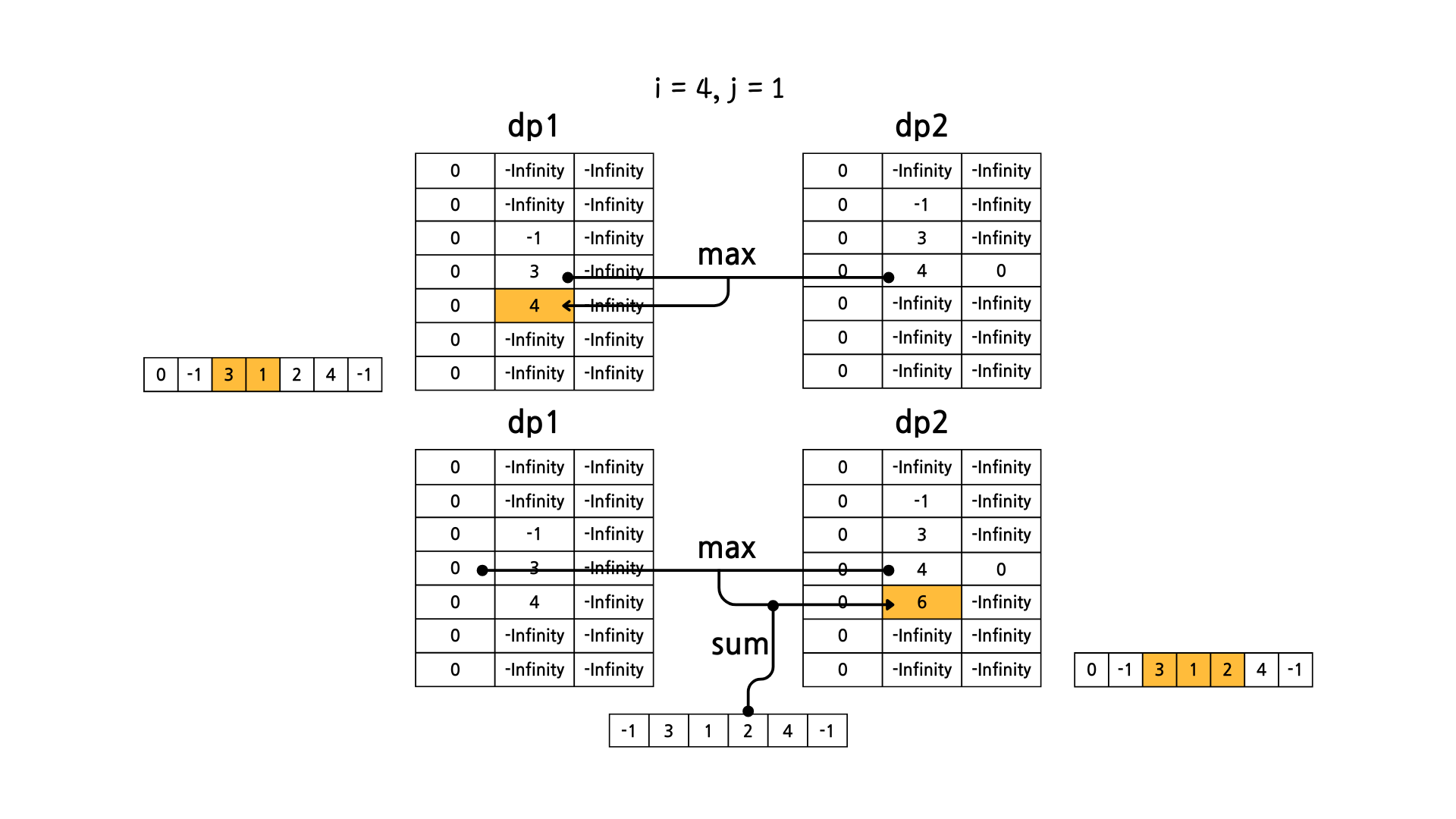
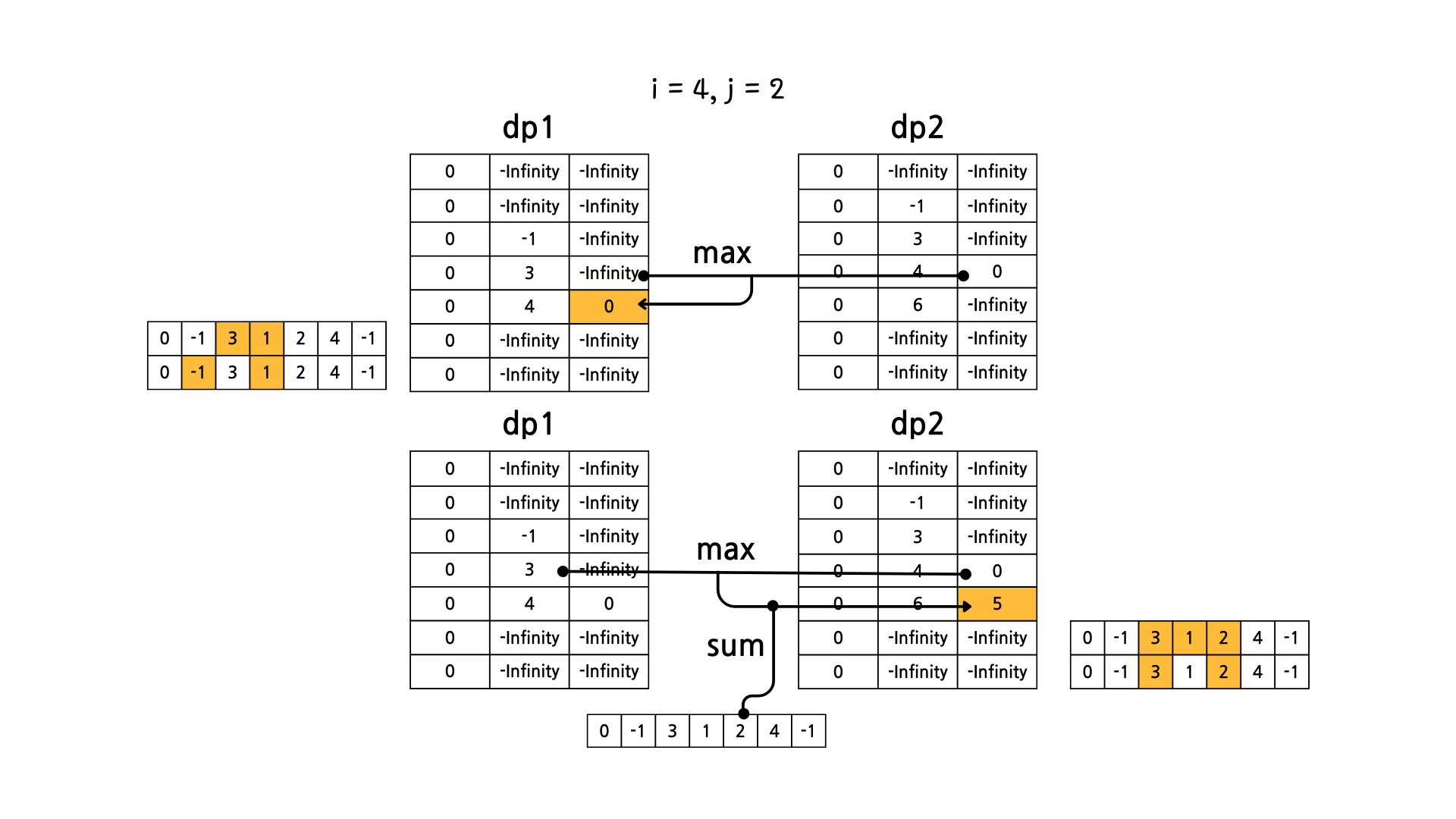
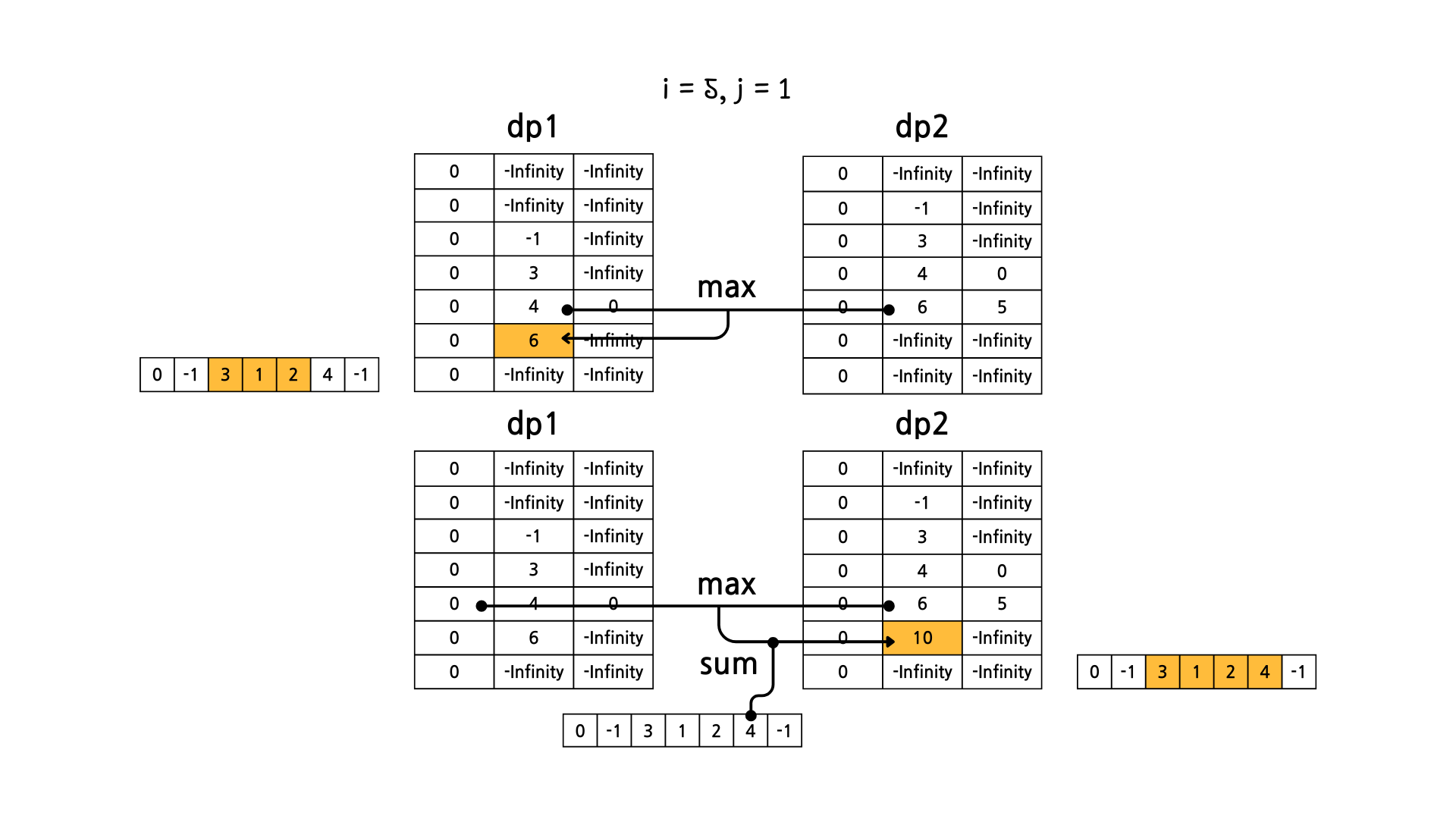
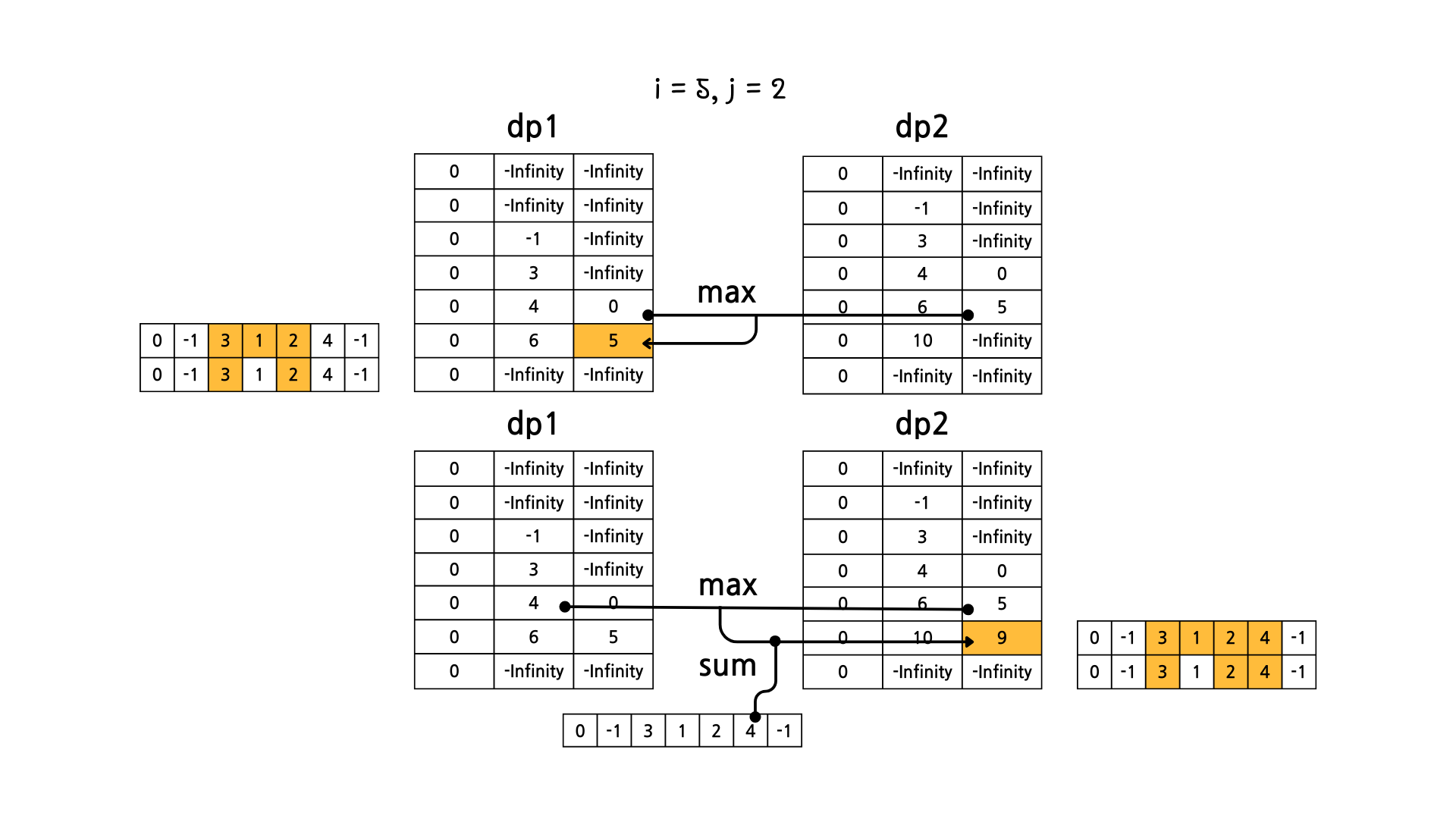
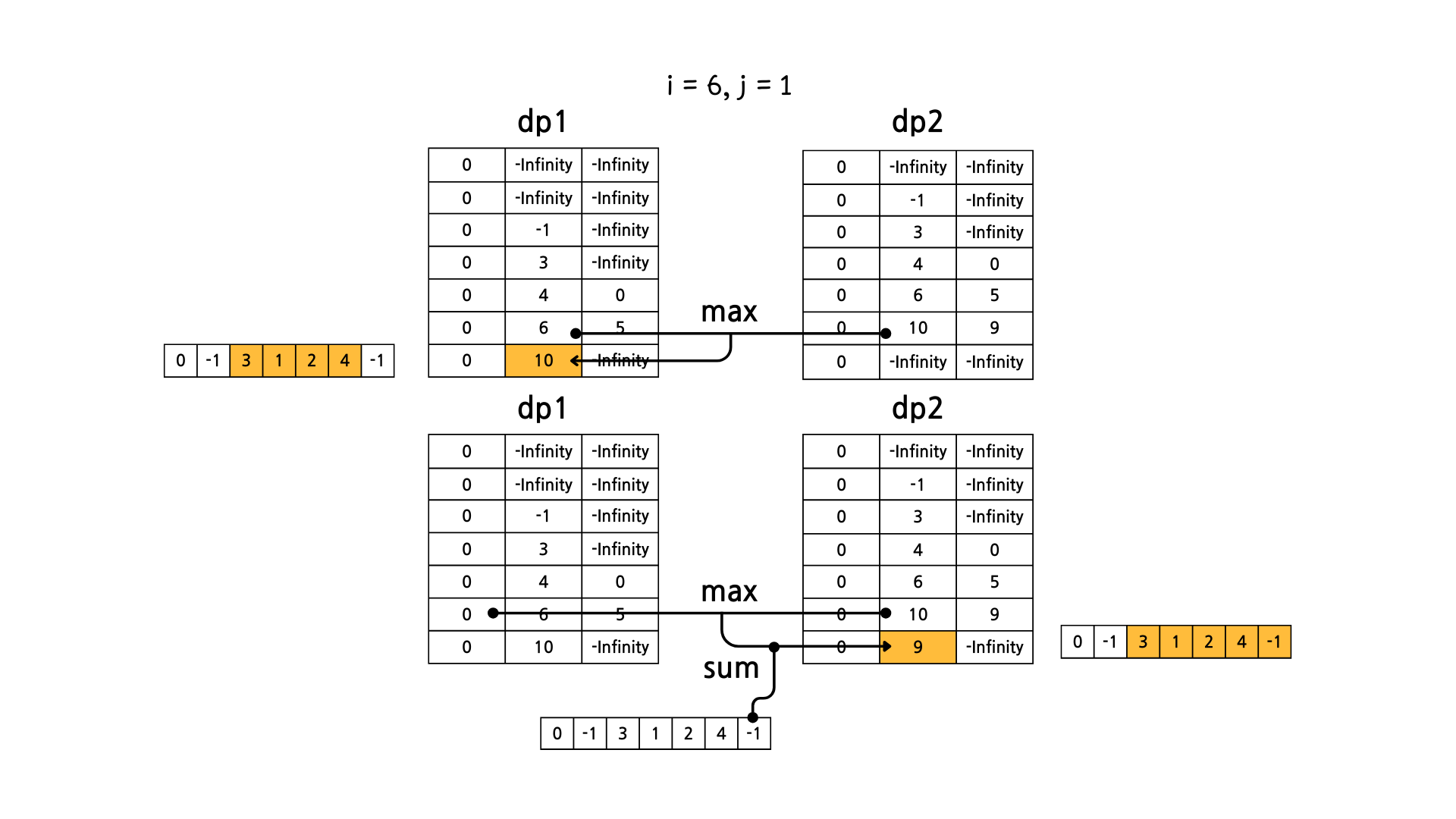
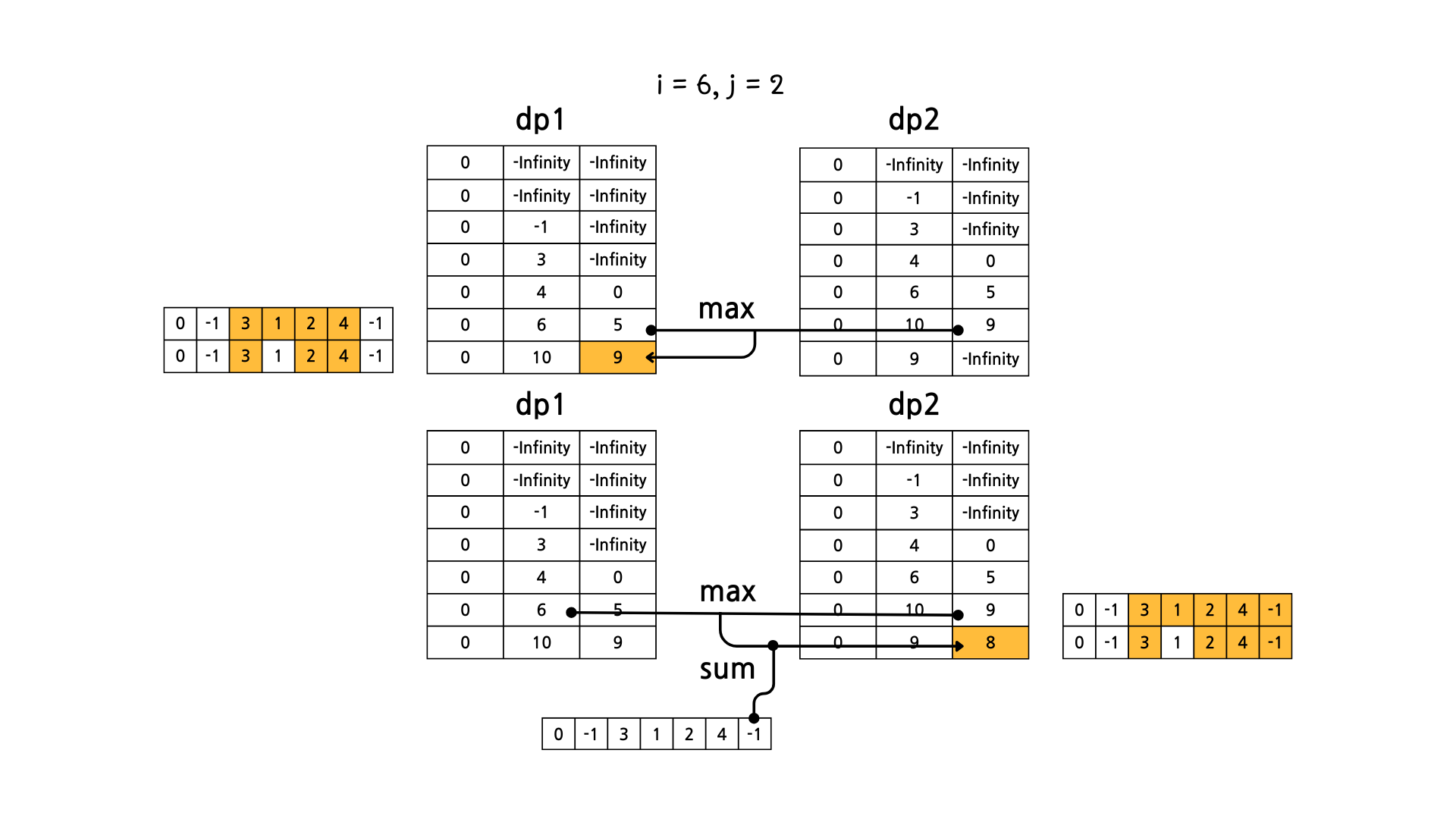
이렇게 해서 dp1[N][M] 과 dp2[N][M] 중에서 더 큰 값을 고르면 정답이 된다.

j가 j <= Math.min(M, Math.ceil(i/2)) 까지 증가하는 이유는 아래와 같다.

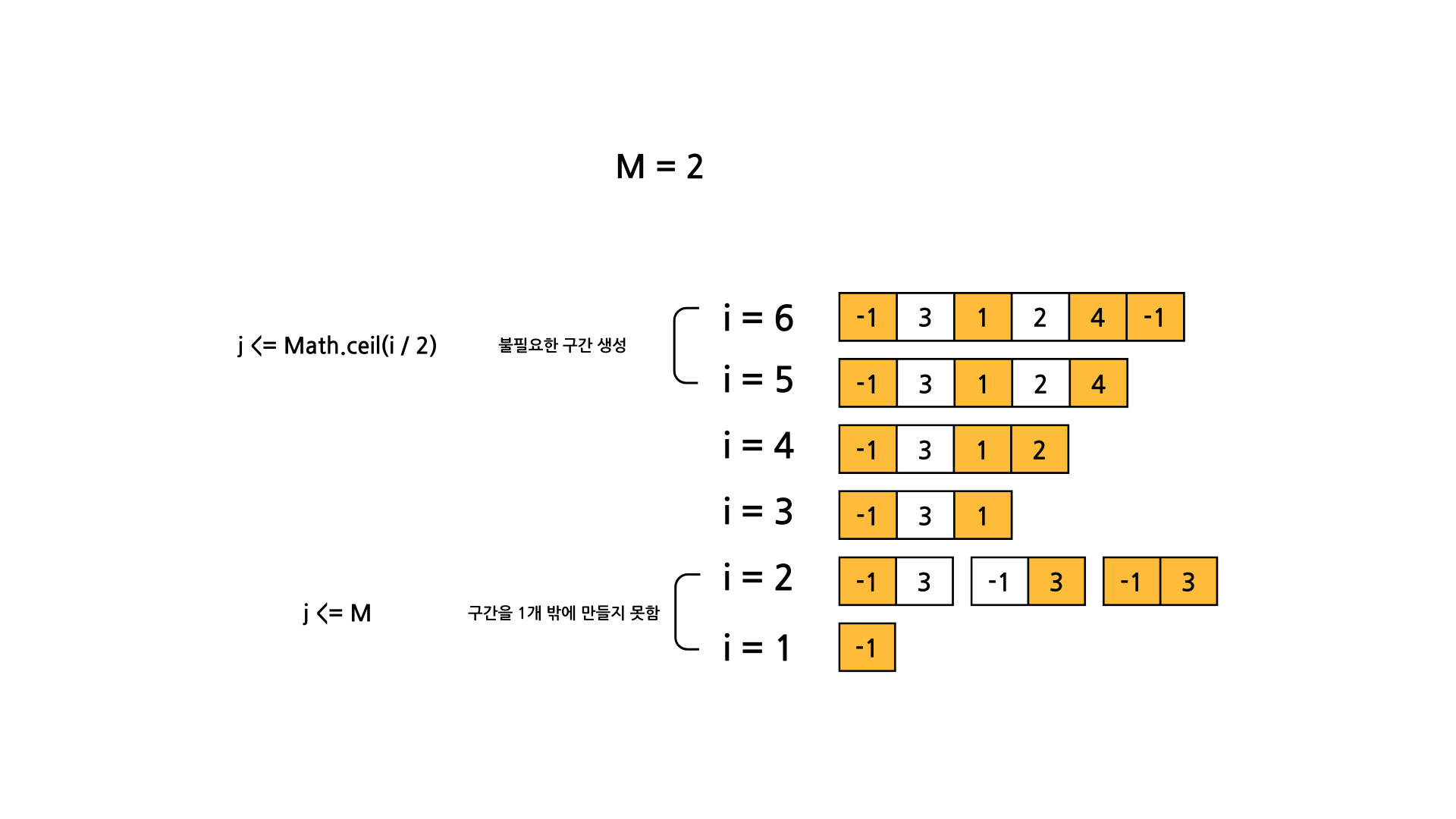
글로 풀어보자면 j가 j <= M 까지 증가할 경우에는 i < M 인 경우에 만들지 못하는 구간을 참조하기 때문에 비효율적으로 동작하고, j <= Math.ceil(i/2) 인 경우에는 Math.ceil(i/2) > M 인 경우에 M개 이상의 구간을 생성함으로써 불필요한 연산을 수행한다.

따라서 j는 j <= Math.min(M, Math.ceil(i/2)) 까지 증가하는 것이다.

참고

https://ddiyeon.tistory.com/62