문제
코드
const filePath = process.platform === 'linux' ? '/dev/stdin' : './Javascript/input.txt';
const input = require('fs').readFileSync(filePath).toString().trim().split('\n');
const N = +input[0];
const circles = input.slice(1).map((e) => e.split(' ').map(Number));
circles.push([0, 0, Infinity]); // 좌표 평면
circles.sort((a, b) => b[2] - a[2]);
const tree = Array.from({ length: N + 1 }, () => []);
const visited = Array(N + 1).fill(false);
let answer = 0;
let start = 0;
dfsConnect(0); // 트리 형성
visited.fill(false);
visited[0] = true;
dfsDepth(0, 0); // 가장 깊은 노드 찾기
visited.fill(false);
dfsDepth(0, start); // 가장 깊은 노드에서 가장 먼 노드 찾기
console.log(answer);
// 부모-자식 연결
function dfsConnect(cur) {
const [x1, y1, r1] = circles[cur];
for (let i = cur + 1; i <= N; i++) {
if (!visited[i]) {
const [x2, y2, r2] = circles[i];
const powX = Math.pow(x1 - x2, 2);
const powY = Math.pow(y1 - y2, 2);
const d = Math.sqrt(powX + powY);
// 내부에 있는 경우라면
if (d < r1) {
tree[cur].push(i);
tree[i].push(cur);
visited[i] = true;
dfsConnect(i);
}
}
}
}
function dfsDepth(depth, cur) {
if (depth > answer) {
answer = depth; // 가장 깊은 노드의 깊이
start = cur; // 가장 깊은 노드의 번호
}
for (let next of tree[cur]) {
if (!visited[next]) {
visited[next] = true;
dfsDepth(depth + 1, next);
visited[next] = false;
}
}
}
코드 설명
이 문제의 핵심은 두 점 사이에 거리를 계산한 뒤 포함 관계인지 확인하여 트리를 만들어 주는 것이다.
문제에서 원들은 내접, 외접 등 교점이 존재하지 않기 때문에 임의의 두 개의 원이 주어졌을 때 한 원이 다른 원의 내부에 있거나, 외부에 있거나 둘 중 하나인 경우만 존재한다는 뜻이다.
그림으로 보면 아래와 같은 경우는 존재하지 않고,
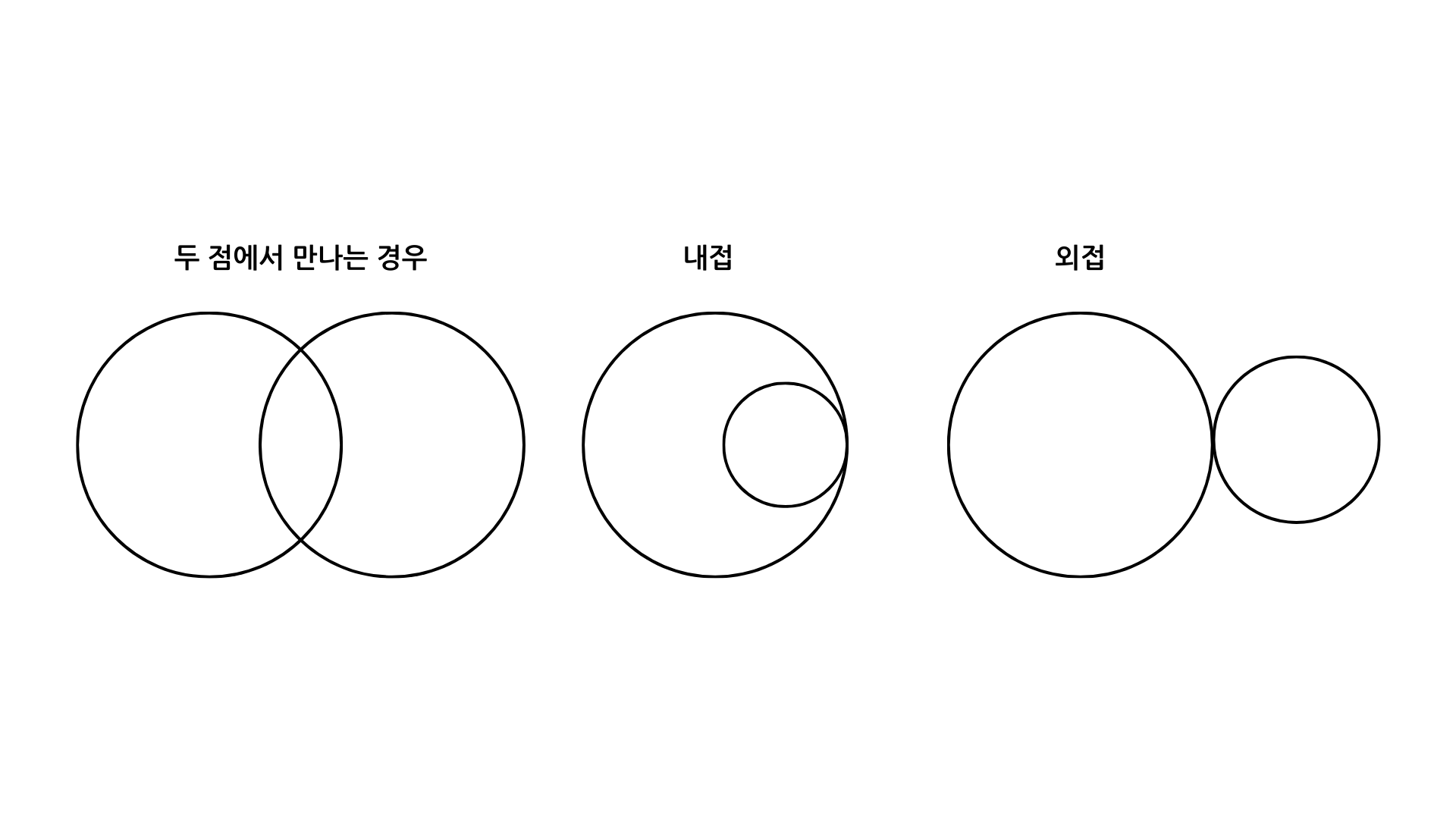
아래의 경우만 존재한다.
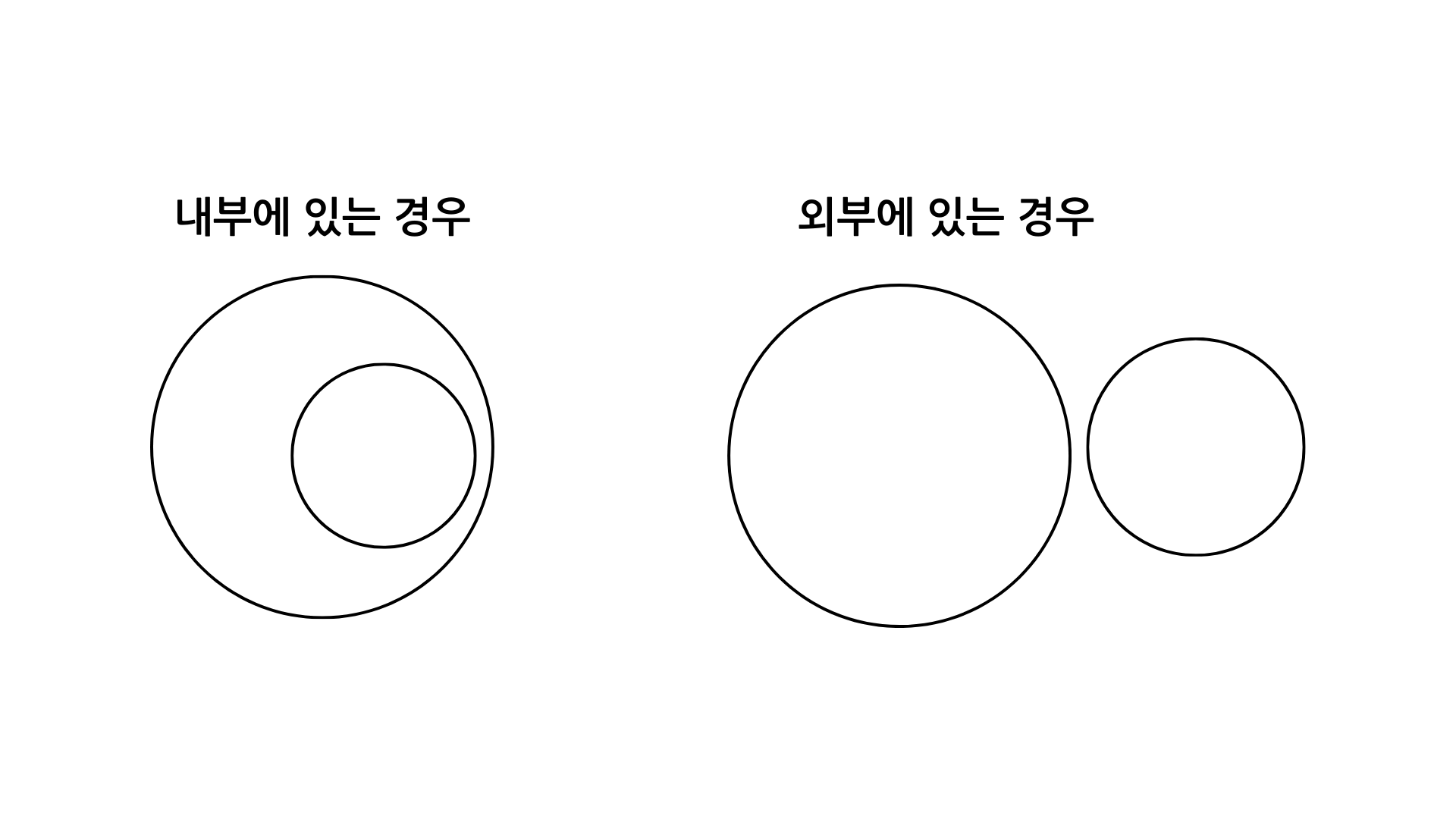
그리고 이 사실을 이용해서 원이 내부에 있는 경우 반지름이 큰 원은 부모, 작은 원을 자식으로 하여 아래와 같이 트리를 만들수 있다.
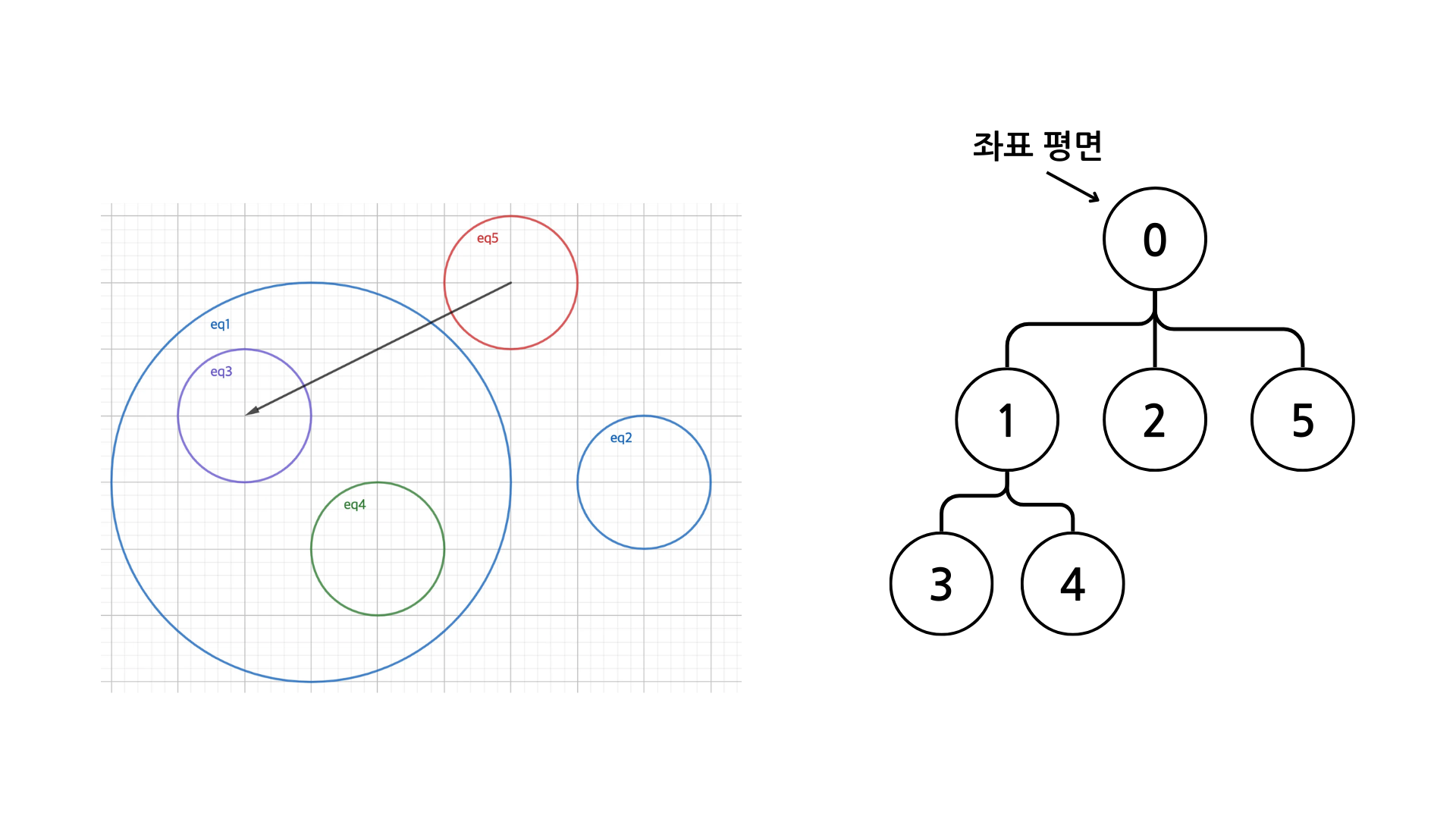
이제 이걸 코드로 구현해보자면,
우선 좌표평면도 큰 원으로 치기 때문에 좌표 평면의 x좌표, y좌표, 반지름도 원의 정보가 저장되어있는 변수에 추가해준다.
circles.push([0, 0, Infinity]); // 좌표 평면그리고 트리는 반드시 직계 부모-직계 자식 노드 관계로 이어져야 하기 때문에 원의 반지름을 기준으로 내림차순 정렬해준다.
만약 입력이 아래와 같이 주어졌다고 가정해보자.
7
4 8 4
5 9 2
9 1 1
6 7 10
3 1 2
5 9 1
6 0 1위 입력값을 이미지로 보자면 아래와 같은 형태를 띈다.
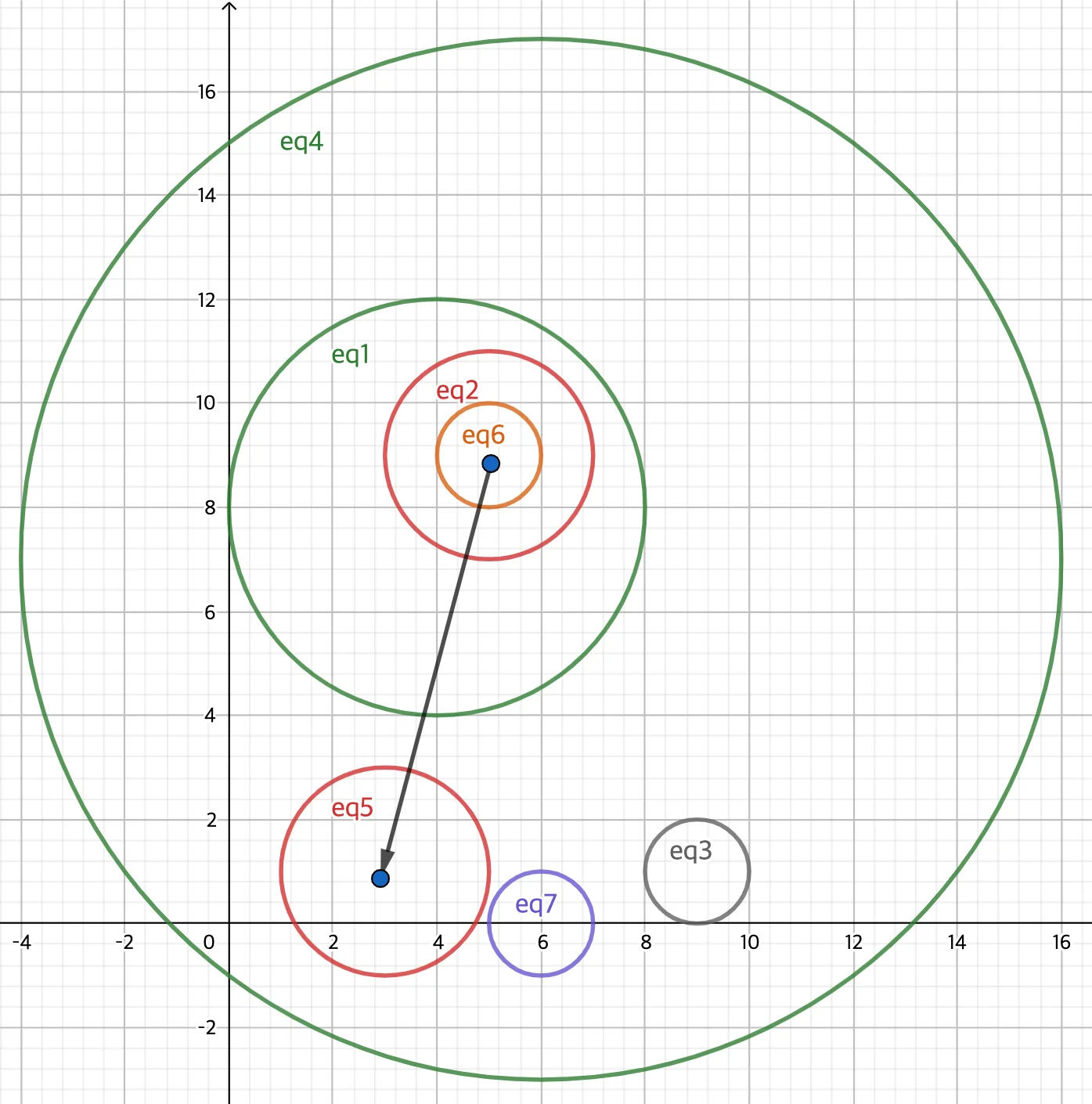
이걸 정렬을 수행하지 않고 트리로 만들어준다면 입력 순서대로 포함 관계 여부를 확인할 것이고 아래와 같은 트리가 생성된다.
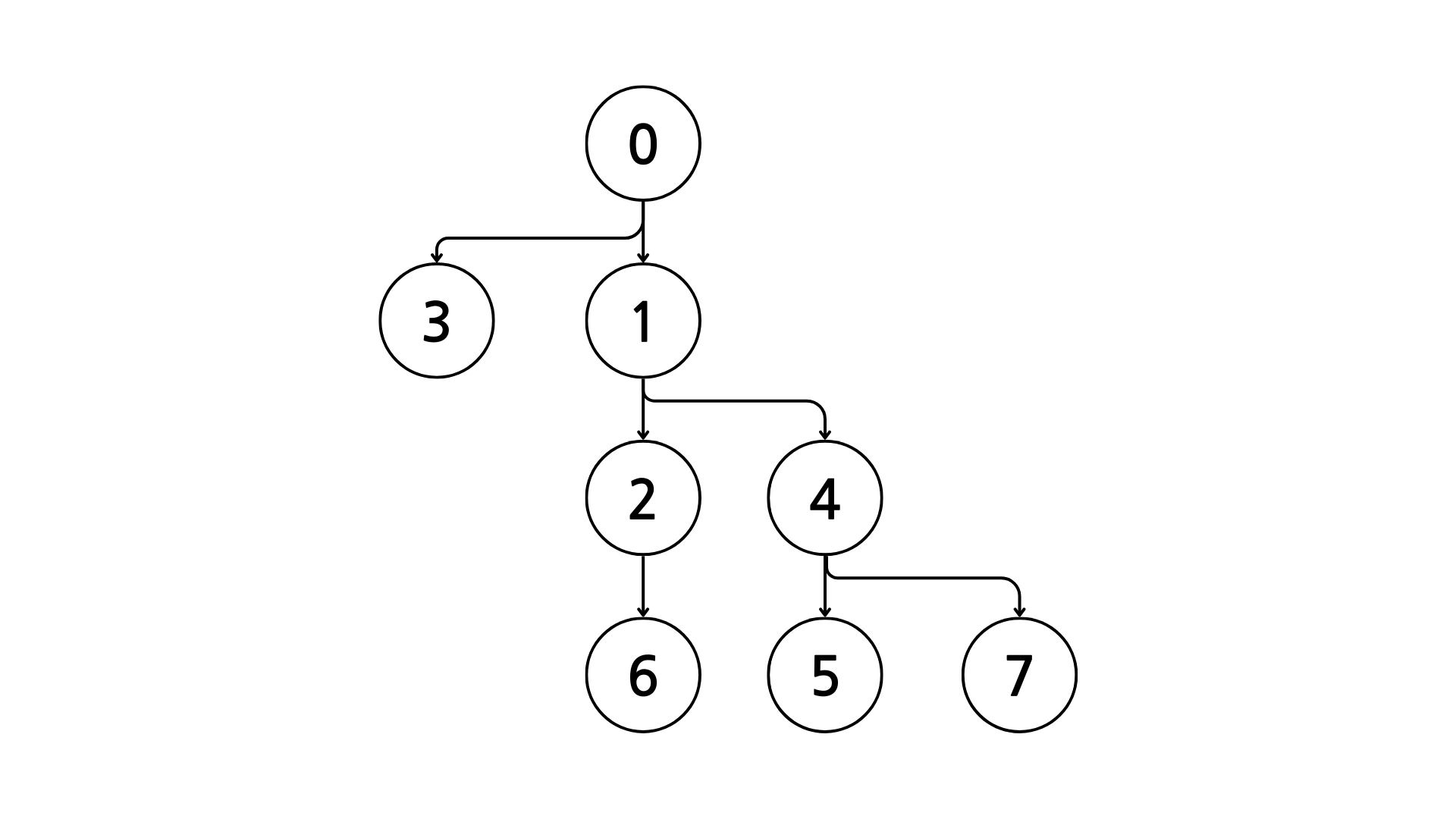
하지만 실제로는 아래와 같은 형태를 띄어야 한다.
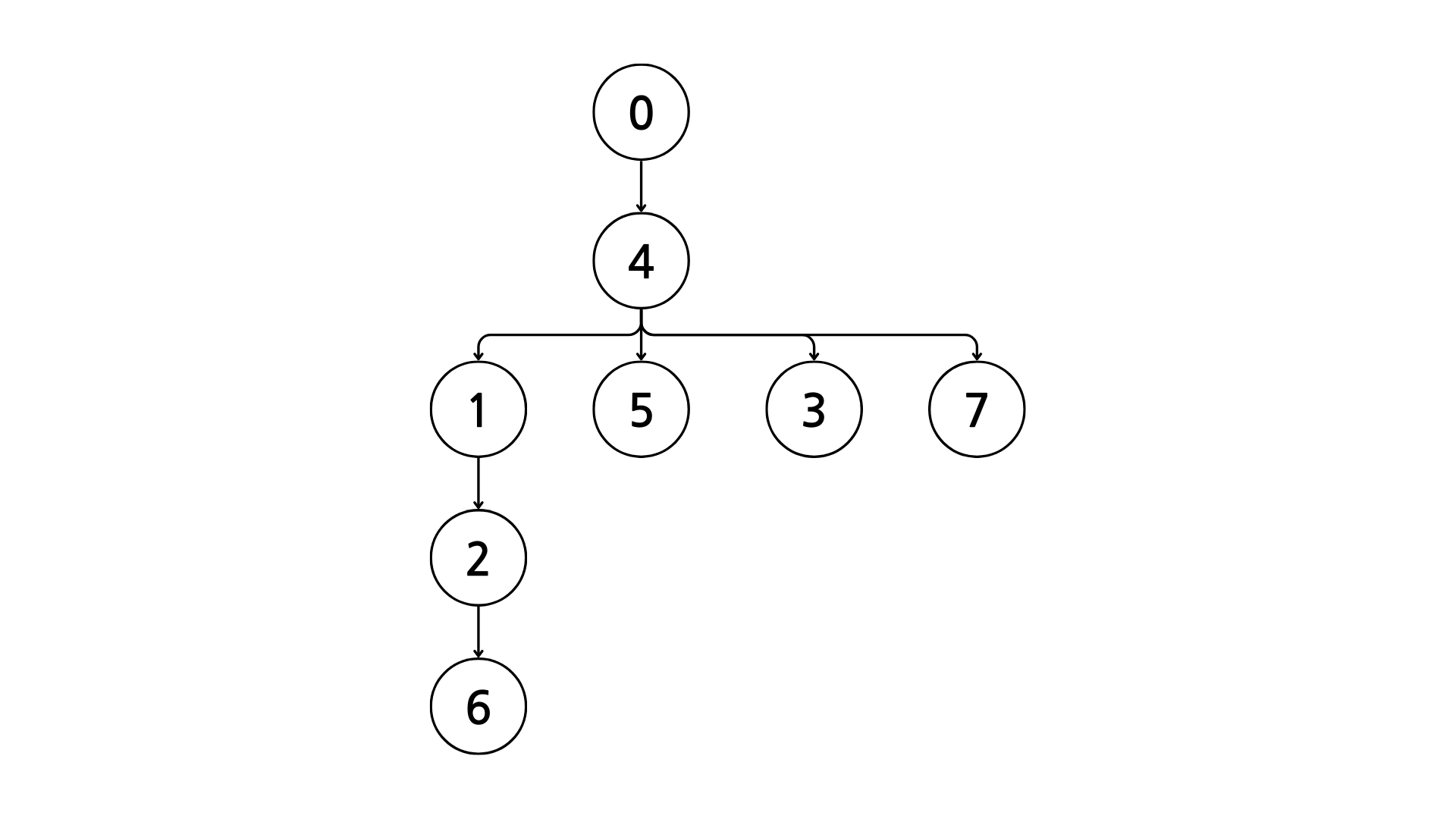
따라서 정렬을 수행해주는 것이다.
circles.sort((a, b) => b[2] - a[2]);그리고 트리를 형성하는 코드를 작성해준다.
// 부모-자식 연결
function dfsConnect(cur) {
const [x1, y1, r1] = circles[cur];
for (let i = cur + 1; i <= N; i++) {
if (!visited[i]) {
const [x2, y2, r2] = circles[i];
const powX = Math.pow(x1 - x2, 2);
const powY = Math.pow(y1 - y2, 2);
const d = Math.sqrt(powX + powY);
// 내부에 있는 경우
if (d < r1) {
tree[cur].push(i);
tree[i].push(cur);
visited[i] = true;
dfsConnect(i);
}
}
}
}
dfsConnect(0);문제의 힌트에 나와있는 '두 점 사이의 거리'를 구하는 공식과

'원이 내부에 있는 경우' 공식을 이용해서

원이 내부에 있다면 두 원을 부모-자식 관계로 연결한다.
위 코드에서는 원이 내부에 있는 경우인지 판별하기 위해 if (d < r1) 로 작성했지만 공식에 나와있는 그대로 if(Math.abs(r1 - r2)) 이렇게 작성해도 된다.
그리고 이제 가장 깊이 있는 노드를 찾아야 한다.
가장 깊은 노드는 일반적인 DFS방식을 사용해서 찾을 수 있다.
우선 트리를 연결할 때 사용했던 visited 변수를 초기화 해주고
visited.fill(false);메인 로직을 작성해준다.
function dfsDepth(depth, cur) {
if (depth > answer) {
answer = depth; // 가장 깊은 노드의 깊이
start = cur; // 가장 깊은 노드의 번호
}
for (let next of tree[cur]) {
if (!visited[next]) {
visited[next] = true;
dfsDepth(depth + 1, next);
visited[next] = false;
}
}
}
dfsDepth(0, 0); // 가장 깊은 노드 찾기하지만 여기서 한 가지 더 추가해주어야 할 것이 있다.
visited[0] = true;dfsDepth()를 실행시키기 전에 위 코드처럼 0번 노드를 방문처리 해주어야 한다.
왜냐하면 트리를 형성해줄 때 부모-자식 노드를 양방향으로 연결했기 때문에 0번 노드에 다른 원이 두 개 이상 연결 되어 있다면 아래 이미지처럼 다시 0번 노드로 나갔다가 0번 노드에 연결되어 있는 다른 원에 먼저 방문하게 되므로 잘못된 깊이 정보가 저장되기 때문이다.
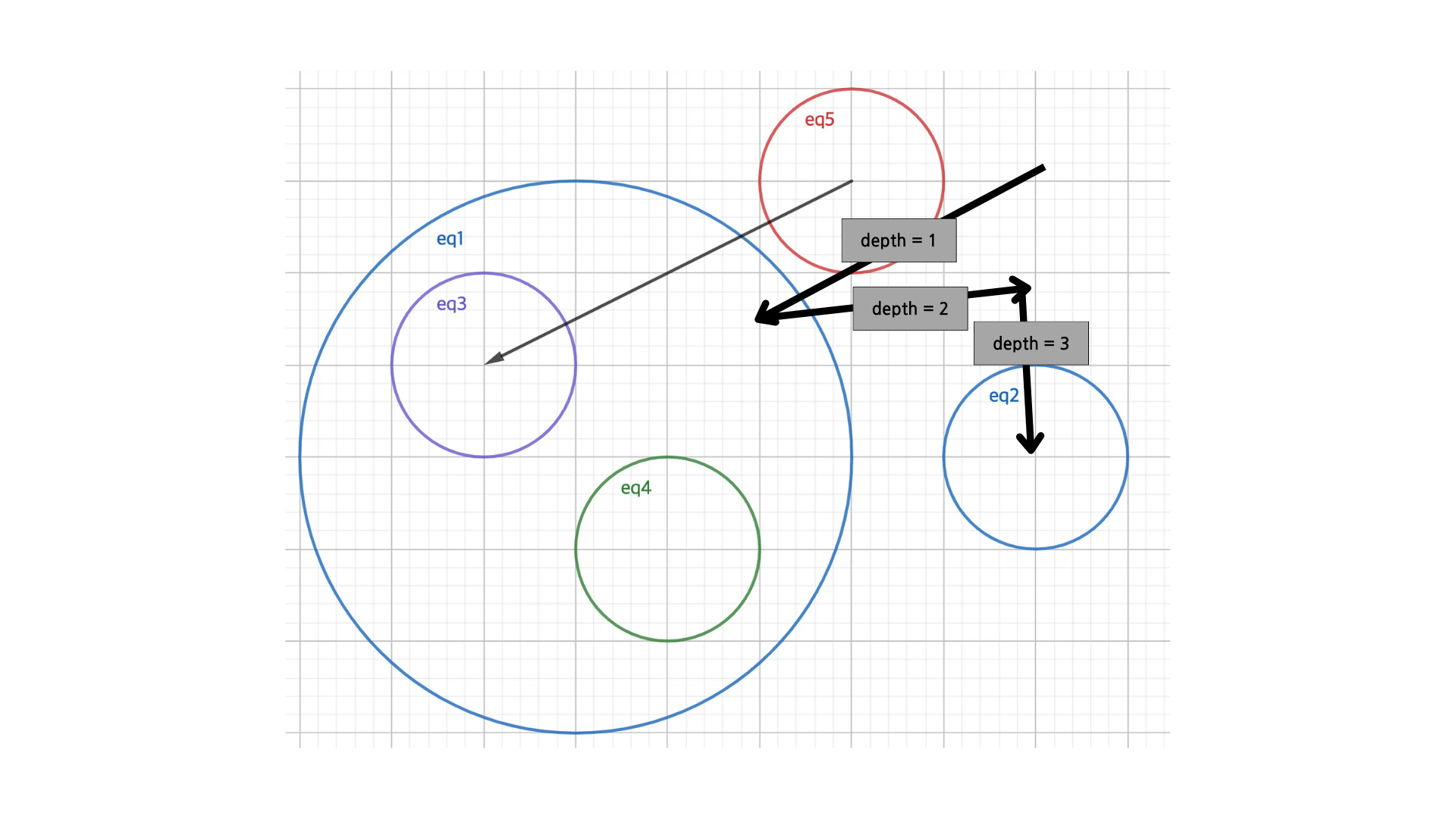
따라서 위 코드를 추가해주면 아래 이미지 처럼 올바른 깊이 정보를 얻을 수 있다.
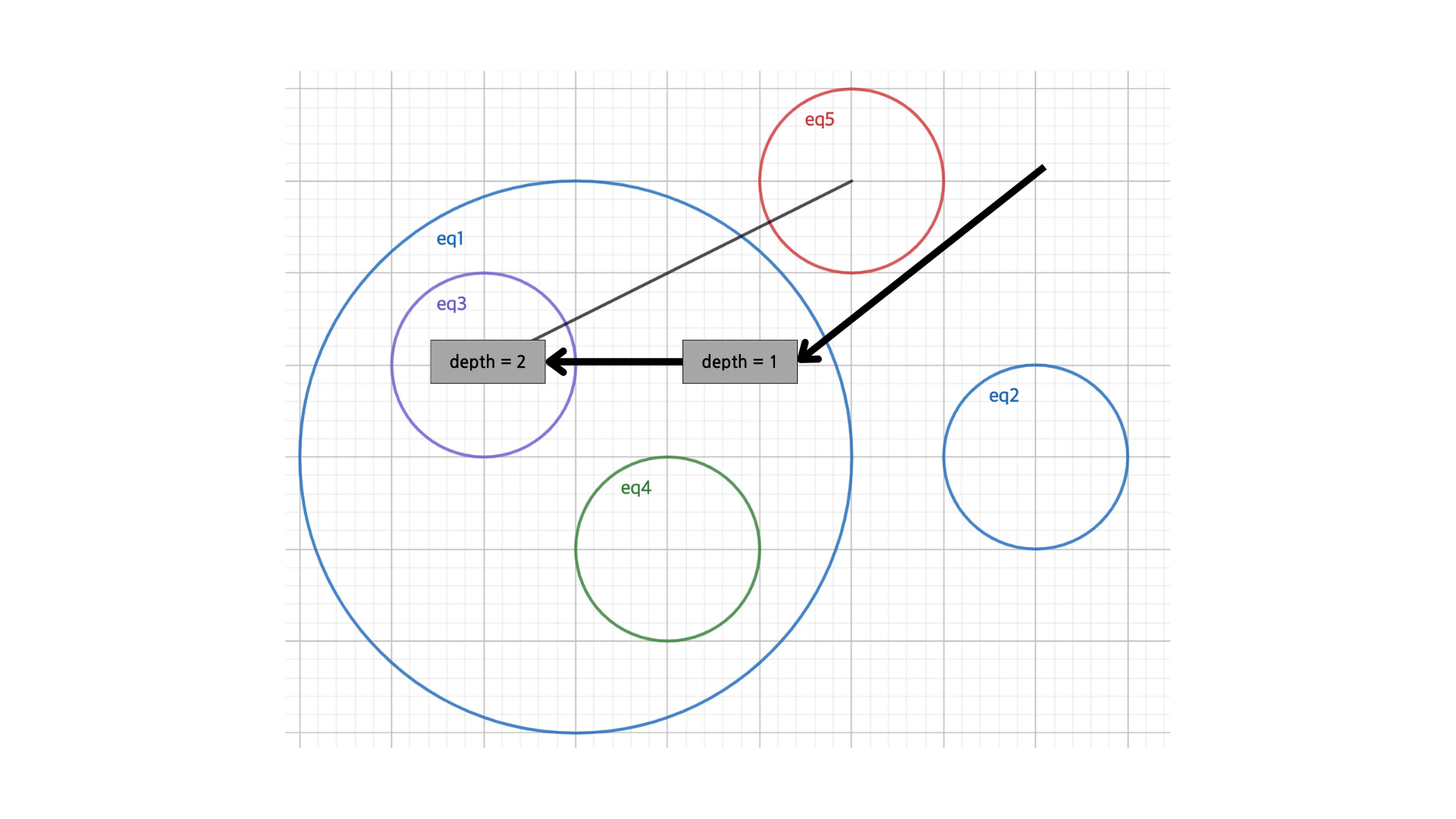
이제 가장 깊이 있는 노드를 찾아주었으니 이제 그 노드에서 가장 멀리 떨어져 있는 노드를 찾으면 가장 큰 이동 횟수를 찾을 수 있다.
방문 정보를 초기화 하고, 이미 만들어둔 dfsDepth() 함수를 사용하여 가장 깊은 노드부터 출발하면 된다.
visited.fill(false);
dfsDepth(0, start); // 가장 깊은 노드에서 가장 먼 노드 찾기

