[백준] 22948_원 이동하기 2 (Javascript)

잭슨·2024년 2월 28일

백준 알고리즘 자바스크립트

알고리즘 문제 풀이

목록 보기

46/130

문제

BOJ22948_원 이동하기 2

코드(시간초과)

const filePath = process.platform === 'linux' ? '/dev/stdin' : './Javascript/input.txt';
const input = require('fs').readFileSync(filePath).toString().trim().split('\n');
const N = +input[0];
const circles = input.slice(1, -1).map((e) => e.split(' ').map(Number));
const [A, B] = input.at(-1).split(' ').map(Number);
circles.push([0, 0, Infinity]);
circles.sort((a, b) => b[2] - a[2]);
const graph = Array.from({ length: N + 1 }, () => []);
const visited = Array(N + 1).fill(false);

dfsConnect(0);
visited.fill(false);
let answer = [];
dfs(A, 1, [A]);

// 트리 만들기 O(n^2)
function dfsConnect(cur) {
    const [num1, x1, r1] = circles[cur];
    for (let i = cur + 1; i <= N; i++) {
        if (!visited[i]) {
            const [num2, x2, r2] = circles[i];
            const d = Math.abs(x1 - x2);
            if (d < Math.abs(r1 - r2)) {
                visited[i] = true;
                graph[num1].push(num2);
                graph[num2].push(num1);
                dfsConnect(i);
            }
        }
    }
}

function dfs(cur, depth, path) {
    if (cur === B) {
        answer = JSON.parse(JSON.stringify(path));
        return;
    }
    for (let next of graph[cur]) {
        if (!visited[next]) {
            visited[next] = true;
            path.push(next);
            dfs(next, depth + 1, path);
            visited[next] = false;
            path.pop();
        }
    }
}
console.log(answer.length);
console.log(...answer);

시간 복잡도

원 이동하기 1 처럼 원의 내부의 있는 경우와 외부의 있는 경우를 고려하여 부모-자식 관계로 트리를 만들고 dfs를 수행했는데 시간초과가 나왔다. N=200,000이라서 트리를 만드는 과정에서 최악의 경우 $O(N^2)$ 이기 때문에 시간초과가 발생하는 것 같다. 그래서 다른 분들의 풀이를 참고해서 풀었다.

코드(맞았습니다)

const filePath = process.platform === 'linux' ? '/dev/stdin' : './Javascript/input.txt';
const input = require('fs').readFileSync(filePath).toString().trim().split('\n');
const N = +input[0];
const arr = input.slice(1, -1).map((e) => e.split(' ').map(Number));
const [A, B] = input.at(-1).split(' ').map(Number);
const visited = Array(N + 1).fill(false);

const circles = [];
for (let [k, x, r] of arr) {
    circles.push([k, x - r]);
    circles.push([-k, x + r]);
}
circles.sort((a, b) => a[1] - b[1]);

const stack = [0];
const tree = Array.from({ length: N + 1 }, () => []);

makeTree();
visited[A] = true;
dfs(A, [A]);

// 괄호쌍 판별 O(n)
function makeTree() {
    for (let [k, _] of circles) {
        if (k < 0) stack.pop();
        else {
            tree[stack.at(-1)].push(k);
            tree[k].push(stack.at(-1));
            stack.push(k);
        }
    }
}

// A -> B 경로 찾기
function dfs(cur, path) {
    if (cur === B) {
        console.log(path.length);
        console.log(...path);
    } else {
        for (let next of tree[cur]) {
            if (!visited[next]) {
                visited[next] = true;
                dfs(next, [...path, next]);
                visited[next] = false;
            }
        }
    }
}

시간 복잡도

시간 초과가 났던 트리를 만드는 부분의 시간 복잡도를 O(N)으로 줄였다. 이 문제는 원 이동하기 1 과는 달리 y축은 0으로 고정되어 있고 x축만 움직인다. 이를 응용해서 트리를 만들어 보자.

풀이

이 문제는 크게 나눴을 때 '트리 만들기' 부분과 'A->B 경로 찾기' 부분으로 나눌 수 있다. 우
선 트리 만들기 부분부터 보자.

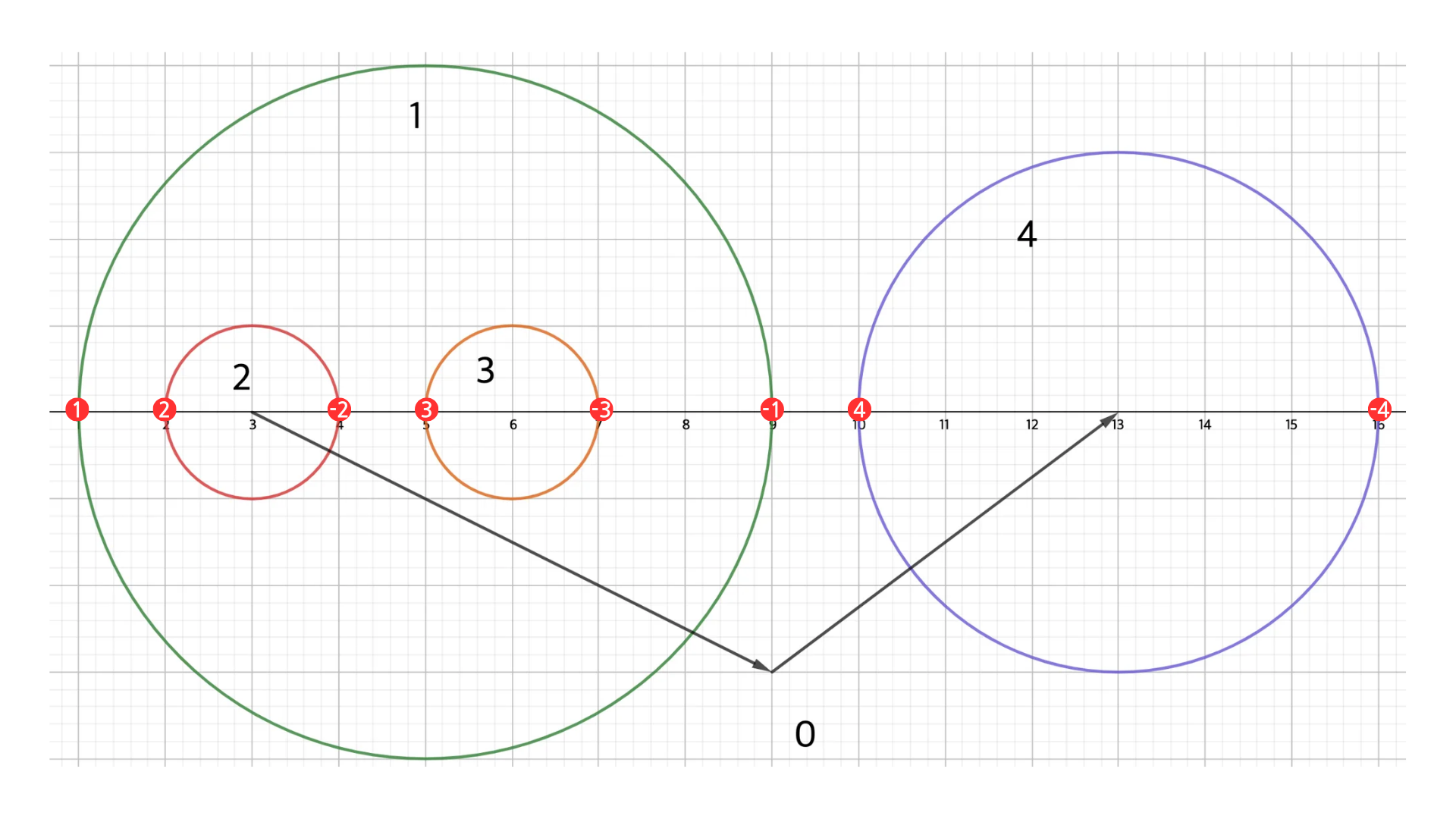
우선 아래와 같이 원들이 있을 때 모든 원들의 왼쪽 지점, 오른쪽 지점을 구한다.
그리고 왼쪽 지점에는 해당 원의 번호, 오른쪽 지점에는 마이너스 부호를 추가한 번호로 지정해서 원의 왼쪽과 오른쪽을 판별한다.

const circles = [];
for (let [k, x, r] of arr) {
    circles.push([k, x - r]);
    circles.push([-k, x + r]);
}

그리고 각각의 지점의 x좌표를 기준으로 오름차순 정렬한다.

circles.sort((a, b) => a[1] - b[1]);

이제 이렇게 정렬된 circles 를 이용해서 왼쪽부터 오른쪽으로 차례차례 모든 지점을 확인할 수 있다.

stack 변수에는 부모 노드의 번호가 저장되고, 루트 노드 즉, 좌표평면의 번호 0을 스택의 초기값으로 넣어둔다.

const stack = [0];

그리고 circles 에 저장되어 있는 원소를 차례차례 확인한다.

makeTree();

function makeTree() {
    for (let [k, _] of circles) {
        if (k < 0) stack.pop();
        else {
            tree[stack.at(-1)].push(k);
            tree[k].push(stack.at(-1));
            stack.push(k);
        }
    }
}