[백준] 3673 나눌 수 있는 부분 수열 (Javascript)

문제

BOJ3673_나눌 수 있는 부분 수열

풀이

요구사항

수열이 주어졌을 때, 연속되는 부분수열의 합이 d로 나누어 떨어지는 부분수열의 개수를 구하시오.

해결방안

2중 반복문 (시간초과)

가장 단순한 방법은
sum(1),
sum(1~2),
sum(1~3),
sum(1~4),
...
sum(1~n)
을 구해서 배열에 저장해놓은 다음,
sum(1) - sum(1),
sum(1~2) - sum(1),
sum(1~3) - sum(1),
...
sum(1~n) - sum(1~n)
을 구하는 방법이다.

하지만 이 방법은 2중 반복문을 사용해야 하기 때문에 $O(N^2)$의 시간이 걸린다. n은 최대 50,000이기 때문에 이 방법은 시간 초과가 난다.

const filePath = process.platform === 'linux' ? '/dev/stdin' : './Javascript/input.txt';
const input = require('fs').readFileSync(filePath).toString().trim().split('\n');
let T = +input[0];
let idx = 1;
let answer = '';

while (T--) {
    let count = 0;
    const [d, n] = input[idx++].split(' ').map(Number);
    const arr = input[idx++].split(' ').map(Number);
    const sum = Array(n + 1).fill(0);
    arr.reduce((acc, cur, i) => {
        sum[i + 1] = acc + cur;
        return acc + cur;
    }, 0);
    for (let i = 0; i <= n; i++) {
        for (let j = 0; j < i; j++) {
            if ((sum[i] - sum[j]) % d === 0) count++;
        }
    }
    answer += count + '\n';
}
console.log(answer.trimEnd());

따라서 다른 방법을 고안해야 한다.

누적합 + 수학

아래와 같은 수열이 있다고 해보자.

2 1 2 1 1 2 1 2

이를 배열에 저장하면 아래와 같은 배열이 만들어질 것이다.

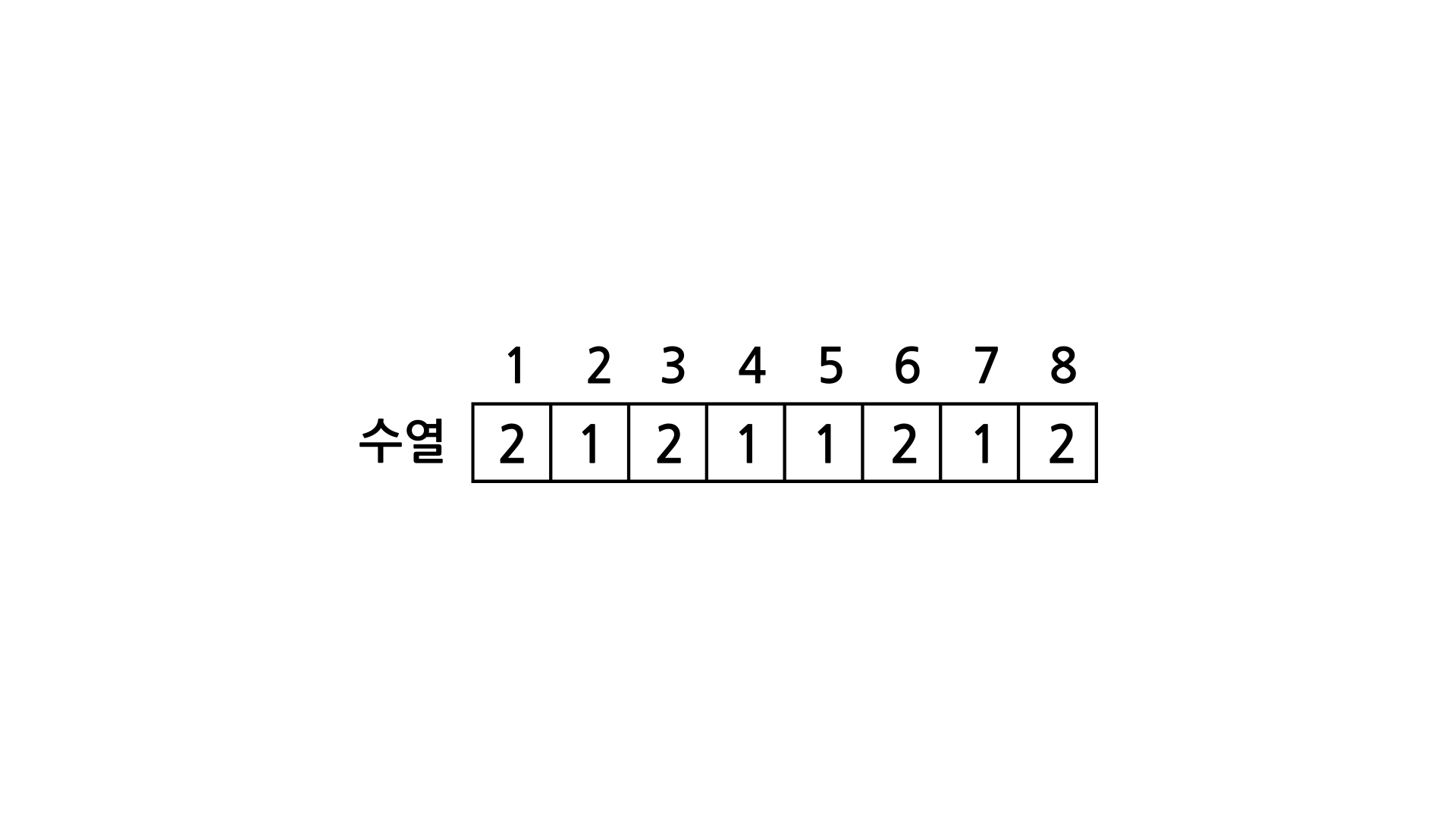
그리고 연속된 부분수열의 합을 구하기 위해 수열의 앞에 있는 숫자부터 차례대로 누적해준다.

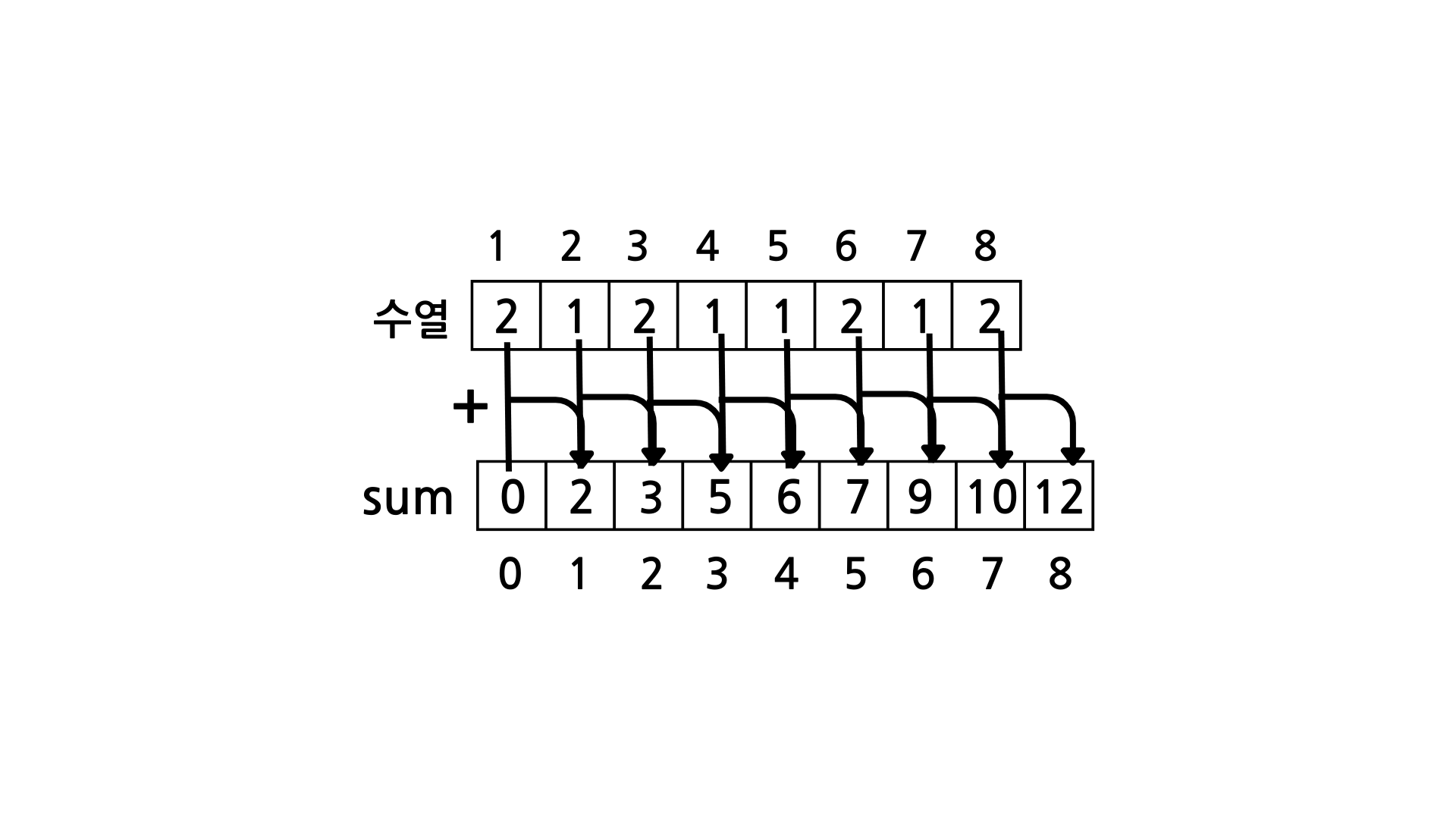
sum은 수열의 '누적합'이 저장되는 배열이다.
이제 우리는 수열의 1번부터 n번까지의 누적합에 접근할 수 있게 되었다.

예를 들어 1번부터 4번까지 수열의 합, 즉 2+1+2+1이 궁금하다면 sum[4]를 참조하면 되고, 1번부터 8번까지의 합이 궁금하면 sum[8]을 참조하면 된다.

하지만 sum 배열은, 1번 수열부터 시작하는 누적합만 참조할 수 있다. 3번부터 5번 수열까지의 합이 궁금할 때는 sum(1~5) - sum(1~2)을 해주면 되지만 이것을 그대로 구현하면 아까 위에서 본 것과 같이 시간초과가 난다.

이건 각 누적합의 나머지를 이용하면 시간초과 없이 해결할 수 있다.

예를 들어 d=4이고, 아래와 같이 각 누적합에 d를 나눈 나머지를 배열에 저장했다고 해보자.

sum[i]는 수열 1번부터 i번까지의 합이다.
그럼 나머지[i]는 1번부터 i번까지의 합에 d를 나눈 나머지다.

이를 기억하고 이어서 진행해보자.

위 나머지 배열을 보면 나머지 값들이 겹치는 요소들이 있다.
나머지 값들이 겹치는 요소를 정리해보면 아래와 같다.

나머지 0: sum[8]
나머지 1: sum[3], sum[6]
나머지 2: sum[1], sum[4], sum[7]
나머지 3: sum[2], sum[5]

이렇게 나머지가 동일한 요소들이 2개 이상 있을 경우 d로 나누었을 때 나누어떨어지는 부분 수열을 구할 수 있다.

예를 들어보자.
sum[6]과 sum[3]은 나머지가 1이다.
sum[6] - sum[3]을 하면 나머지가 0이 된다.
즉 d로 나누었을 때 나머지가 같은 수열의 합끼리 뺄셈을 해주면 0이 된다.

sum(1~6) - sum(1~3) = sum(4~6)

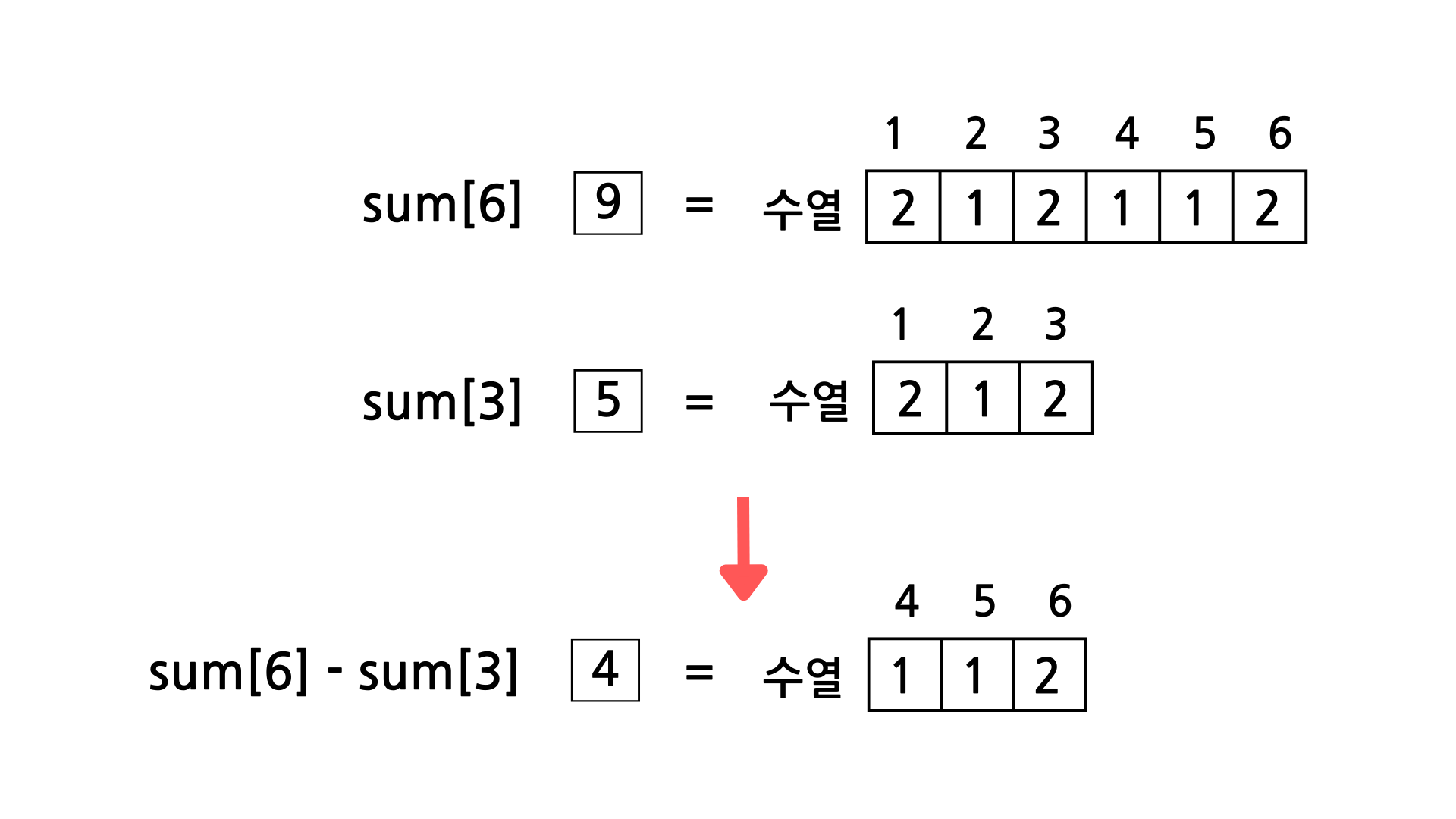
즉 부분수열 sum(4~6)=4이므로 4로 나누었을때 나누어 떨어진다.

이런식으로 반복해서 수행해주면 d로 나누어 떨어지는 수열의 합의 개수를 구할 수 있다.

위와 같은 방식으로 나누어 떨어지는 부분수열들을 더 찾아보자.

// 나머지 0
sum(1~8) = sum(1~8)

// 나머지 1
sum(1~6) - sum(1~3) = sum(4~6)

// 나머지 2
sum(1~7) - sum(1~4) = sum(5~7)
sum(1~7) - sum(1~1) = sum(2~7)
sum(1~4) - sum(1~1) = sum(2~4)

// 나머지 3
sum(1~5) - sum(1~2) = sum(3~5)

이를 통해 총 6개의 부분수열의 합이 d로 나누어 떨어짐을 알 수 있다.

나머지가 0인 합은 1개밖에 없지만, 이미 나머지가 0이기 때문에 그냥 합의 개수만큼 카운트를 증가시켜주면 된다.

그 외 나머지가 1 이상인 것들은 개수가 2개 이상일 때, 한 개씩 카운트를 증가시켜주면 된다.

이를 코드로 구현해보자.

코드

const filePath = process.platform === 'linux' ? '/dev/stdin' : './Javascript/input.txt';
const input = require('fs').readFileSync(filePath).toString().trim().split('\n');
let T = +input[0];
let idx = 1;
let answer = '';

while (T--) {
    let count = 0;
    const [d, n] = input[idx++].split(' ').map(Number);
    const arr = input[idx++].split(' ').map(Number);
    const sum = Array(n + 1).fill(0);
    const mod = new Map();

	// 핵심 로직
    arr.reduce((acc, cur, i) => {
        sum[i + 1] = acc + cur;
        const remainder = sum[i + 1] % d;
        if (remainder === 0) count++;
        if (mod.has(remainder)) {
            count += mod.get(remainder);
            mod.set(remainder, mod.get(remainder) + 1);
        } else {
            mod.set(remainder, 1);
        }
        return acc + cur;
    }, 0);

    answer += count + '\n';
}
console.log(answer.trimEnd());

sum[i] = 1번부터 i번까지 수열의 누적합
remainder[i] = sum[i]를 d로 나누었을 때 나머지
mod.get(i) = 나머지가 i인 합의 개수

이렇게 이해하고 핵심 로직부분을 순서도로 작성해보자.

1. 입력으로 주어진 수열을 reduce 메서드를 통해 순회하며 누적합을 sum 배열에 저장한다.
2. 누적합을 저장함과 동시에 해당 누적합을 d로 나누었을 때의 나머지를 remainder에 저장한다.
3. 나머지가 0이라면 카운트를 1 증가시킨다.
4. 나머지가 mod 에 저장되어 있는지 확인한다.
   4-1. 만약 저장되어 있다면 저장되어 있는 개수만큼 카운트를 증가시키고, 저장되어 있는 개수도 1개 증가시킨다.
   4-2. 만약 저장되어 있지 않다면 새로 저장해준다 (개수를 1로 만듦).
5. reduce가 끝날 때까지 반복한다.

위 순서도에서 4-1번이 이해가 잘 안될 수도 있다.
4-1 번을 이해하기 위해서 작게 쪼개어서 살펴보자.

1. if (mod.has(remainder))
   이 부분은 나머지가 같은 합이 이미 mod에 저장되어 있는가 확인하는 부분이다. 이는 나머지가 동일한 합이 2개 이상일 때만 카운트를 증가시키도록 만들어준다.
2. count += mod.get(remainder)
mod.set(remainder, mod.get(remainder) + 1)
   기존에 mod에 저장되어 있던 나머지가 동일한 요소의 개수만큼 카운트를 증가시킨다. 카운트를 기존에 있던 나머지의 개수만큼 증가시키는 이유는 나머지가 동일한 요소가 한 개씩 증가할 때마다, 기존에 있던 나머지의 개수만큼 조합 가능한 경우의 수가 증가하기 때문이다.

코드 (왜 틀렸지?)

아래 코드는 누적합을 전부 구한 뒤에 따로 나머지가 동일한 요소들의 조합의 개수를 구해주는 코드다.

나머지가 동일한 요소가 n개 있을 때, 수열을 2개씩 뽑아서 뺄셈을 하는 것이기 때문에 조합의 개수는 $nC_2$가 된다.

d가 1일 때는 모든 수열의 합이 나누어 떨어지기 때문에 따로 빼줘서 처리를 하도록 했다.

하지만 계속 틀렸다고 나온다.
여러 예시를 시도해봤지만 반례를 못찾겠다...

const filePath = process.platform === 'linux' ? '/dev/stdin' : './Javascript/input.txt';
const input = require('fs').readFileSync(filePath).toString().trim().split('\n');
let T = +input[0];
let idx = 1;
let answer = '';

while (T--) {
    const [d, n] = input[idx++].split(' ').map(Number);
    const arr = input[idx++].split(' ').map(Number);
    const sum = Array(n + 1).fill(0);
    const mod = Array(d).fill(0);

    arr.reduce((acc, cur, i) => {
        sum[i + 1] = acc + cur;
        const remainder = sum[i + 1] % d;
        mod[remainder]++;
        return acc + cur;
    }, 0);

    let count = 0;
    if (d === 1) {
        count += mod[0];
        count += (mod[0] * (mod[0] - 1)) >> 1;
    } else {
        for (let i = 0; i < d; i++) {
            if (i === 0) count += mod[i];
            else if (mod[i] > 1) count += (mod[i] * (mod[i] - 1)) >> 1;
        }
    }

    answer += count + '\n';
}
console.log(answer.trimEnd());

시도해본 반례

-예시 1-

1
1 2
1 2

correct: 3

-예시 2-

1
1 3
1 2 3

correct: 6

-예시 3-

1
2 3
1 2 3

correct: 2