[백준] 4811 알약 (Javascript)

문제

BOJ4811_알약

풀이

문제 정의

알약이 N개 있고, 하루마다 알약을 반 개씩 먹는다. 만약 한 개가 통째로 있는 알약을 집었다면 반으로 쪼개서 반은 먹고 반은 다시 둔다. 만약 반 개 짜리 알약을 집었다면 그대로 알약을 먹는다.

한 개 짜리를 집은 날에는 'W'라는 글자를 적고, 반 개 짜리를 집은 날에는 'H'라는 글자를 종이에 적는다.

최종적으로 N개의 알약을 다 먹었을 때 종이에는 하나의 문자열이 완성된다. 이때 가능한 문자열의 모든 경우의 수를 구하는 문제다.

해결방안

온전한 알약과 반쪽짜리 알약의 개수를 따로 저장하기 위해 두개의 변수whole, half를 만들어주자.

n=4라고 가정했을 때, 초기에는 whole=4, half=0 이다. 이 풀이를 진행해 나가면 아래 그림과 같은 흐름으로 진행될 것이다.

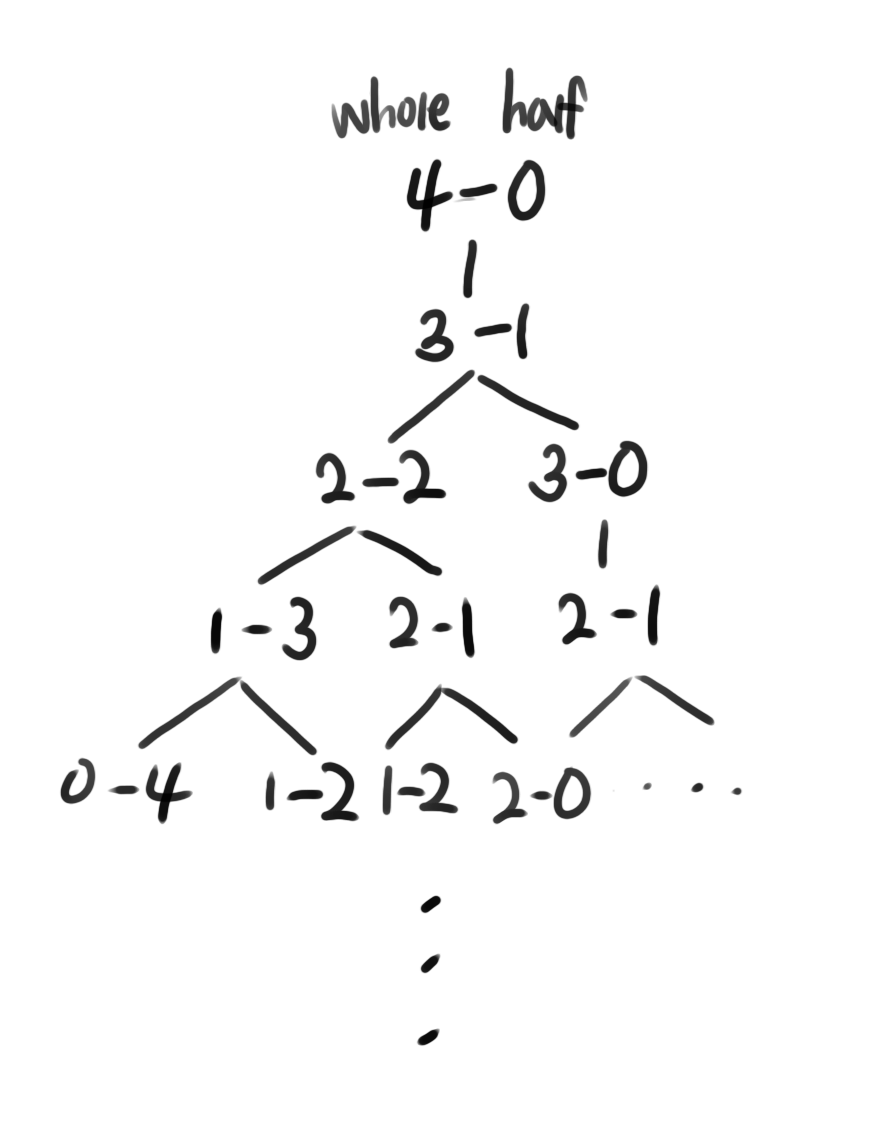
위 그림을 보면 중복된 연산들이 겹치는 걸 볼 수 있다.

만약 완전탐색을 통해 모든 경우의 수를 찾는다면 시간 복잡도는 $O(2^n)$ 이고, 테스트케이스 하나당 $n\le30$ 이기 때문에 완전탐색으로 풀 경우 시간초과가 난다.

따라서 이 문제는 메모이제이션 기법을 이용해서 DP로 풀어주면 된다.

이제 점화식을 새워보자.

2차원 DP배열이 있고 세로축의 인덱스가 나타내는 것은 한 개 짜리 알약의 개수, 가로축의 인덱스가 나타내는 것은 반 개 짜리 알약의 개수라고 했을 때 dp[whole][half] 은 dp[whole][half+1] + dp[whole+1][half-1] 이다.

예를 들어보자.

whole=2, half=1 을 만들 수 있는 경우의 수는 whole=2, half=2 에서 반 쪽 짜리 알약을 하나 먹어서 half-1을 해주거나, whole=3, half=0 에서 하나짜리 알약을 반으로 쪼개 먹어서 whole-1, half+1을 해주는 방법이 있다.

따라서 dp[whole][half] = dp[whole][half+1] + dp[whole+1][half-1] 이다.

또한 초기값은 dp[n][0] = 1 로 초기화 해준다.

그리고 2중 반복문을 통해 배열을 순회하며 값을 갱신해주면 된다.

for (let w = n; w >= 0; w--) {
  for (let h = n; h >= 0; h--) {
    if (h < n) dp[w][h] += dp[w][h + 1];
    if (w < n && h > 0) dp[w][h] += dp[w + 1][h - 1];
  }
}

아까의 예시처럼 n=4라고 했을 때, 반복문이 끝나면 dp배열은 아래 그림과 같이 완성된다.

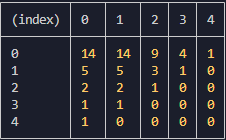
그리고 dp[0][0]에 정답이 저장된다.

전체 코드

const filePath = process.platform === 'linux' ? '/dev/stdin' : './Javascript/input.txt';
const input = require('fs').readFileSync(filePath).toString().trim().split('\n').map(Number);
let answer = '';
for (let i = 0; i < input.length - 1; i++) {
    answer += solution(input[i]);
}

// dp[w][h] += dp[w][h+1] + dp[w+1][h-1]
function solution(n) {
    const dp = Array.from(Array(n + 1), () => Array(n + 1).fill(0));
    dp[n][0] = 1;
    for (let w = n; w >= 0; w--) {
        for (let h = n; h >= 0; h--) {
            if (h < n) dp[w][h] += dp[w][h + 1];
            if (w < n && h > 0) dp[w][h] += dp[w + 1][h - 1];
        }
    }
    return dp[0][0] + '\n';
}

console.log(answer.trimEnd());