[프로그래머스] 유전법칙 (JavaScript)

문제

프로그래머스_유전법칙

코드

function solution(queries) {
    const answer = [];
    const gene = ["RR", "Rr", "Rr", "rr"];
    
    queries.forEach(([n, p])=>{
        answer.push(recursion(n,p));
    })
    
    function recursion(n,p){
        if(n === 1) return "Rr";
        if(n === 2) return gene[p-1];
        
        const peas = recursion(n-1, Math.floor((p-1)/4)+1);
        if(peas === "RR") return "RR";
        else if(peas === "rr") return "rr";
        else return gene[(p-1)%4];
    }
    
    return answer;
}

/*
n=2가 될 때까지 올라가기
    (n=3) 1,2,3,4 -f(x)-> 1 (n=2)
    (n=3) 5,6,7,8 -f(x)-> 2 (n=2)
    (n=3) 9,10,11,12 -f(x)-> 3 (n=2)
    (n=3) 13,14,15,16 -f(x)-> 4 (n=2)
    f(x) = Math.floor((x-1)/4) + 1 = x번째 노드의 부모 노드 순서
n=2일 때, 
    p번 째 완두콩이 RR이면 그 자식은 모두 RR 이므로 answer에 RR 추가
    p번 째 완두콩이 rr이면 그 자식은 모두 rr 이므로 asnwer에 rr 추가
    p번 째 완두콩이 Rr이면 올라온 순서 그대로 다시 내려가기
        1,2,3,4 -f(x)-> 1,2,3,4
        5,6,7,8 -f(x)-> 1,2,3,4
        9,10,11,12 -f(x)-> 1,2,3,4
        13,14,15,16 -f(x) -> 1,2,3,4
        f(x) = (x-1) % 4 + 1
        끝 까지 내려왔을 때, x가 몇이냐에 따라 완두콩의 유전 정보(RR,Rr,rr)를 answer에 추가.
*/

접근법

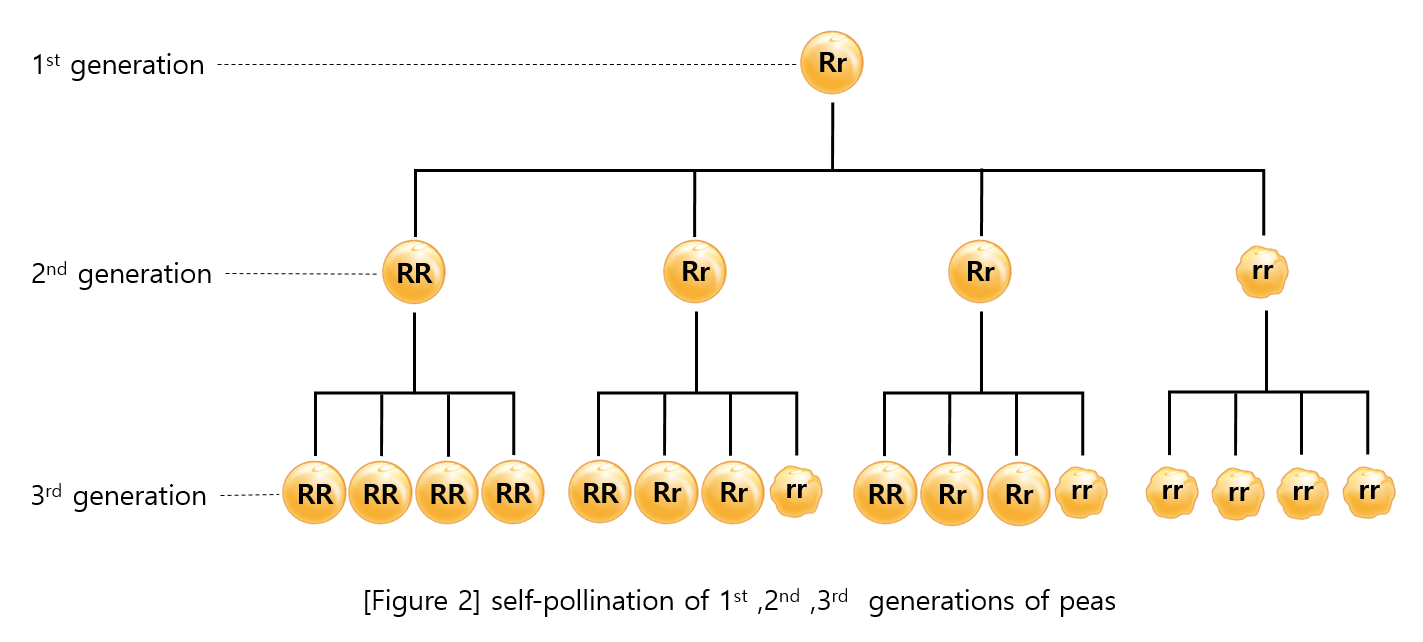
• n이 1일 때는 Rr 밖에 없기 때문에 Rr을 answer에 담는다.
• n이 2일 때는 p번째 유전정보를 고르면 된다. 우리는 배열에 ["RR", "Rr", "Rr", "rr"] 을 저장할 것이기 때문에 p-1 번째 유전정보를 고르면 된다.
• n이 3이상일 때는 n=2가 될 때까지 p번째 완두콩의 부모를 거슬러 올라간다. 거슬로 올라가는 과정은 다음과 같다.

  (n) 1,2,3,4 -f(x)-> 1 (n-1)
  (n) 5,6,7,8 -f(x)-> 2 (n-1)
  (n) 9,10,11,12 -f(x)-> 3 (n-1)
  (n) 13,14,15,16 -f(x)-> 4 (n-1)

  여기서 $f(x)$를 구해보면 $f(x) = Math.floor((x-1)/4) + 1$이 된다. p1 -f(x)-> p2 일 때, p2가 부모 세대의 p2번째 완두콩을 의미한다. 그리고 부모 세대로 올라왔으므로 n은 1을 빼준다.
• n=2가 되었을 때 RR이라면 RR의 자식은 모두 RR이므로 RR을 answer에 담는다. rr일 경우도 같은 이유로 rr을 answer에 담는다. 다만 Rr일 경우에는 올라왔던 순서 그대로 역순으로 내려가면 알 수 있다.
• 현재 세대에서의 p를 통해 하나의 그룹에서 몇 번째 완두콩인지는 다음과 같이 알 수 있다.

  1,2,3,4 -f(x)-> 1,2,3,4
  5,6,7,8 -f(x)-> 1,2,3,4
  9,10,11,12 -f(x)-> 1,2,3,4
  13,14,15,16 -f(x) -> 1,2,3,4

  여기서 $f(x)$를 구해보면 $f(x) = (x-1)$이 된다. p1 -f(x)-> p2 일 때, p2는 현재 하나의 그룹에서 p2번째 완두콩을 의미한다.

참고자료

https://doricoding.tistory.com/191