[프로그래머스] 숫자의 표현 (JavaScript)

잭슨·2025년 2월 22일

등차수열의 합 수학 알고리즘 프로그래머스

알고리즘 문제 풀이

목록 보기

128/130

문제

[프로그래머스] 숫자의 표현

n을 연속된 자연수의 합으로 표현할 수 있는 방법의 수를 찾아내는 문제다.

예시

n = 15

1 + 2 + 3 + 4 + 5 = 15
4 + 5 + 6 = 15
7 + 8 = 15
15 = 15

답: 4

투 포인터 + 등차수열의 합 풀이

function solution(n) {
    var answer = 0;
    const arr = Array.from({length: n+1}, (_, i) => i);
    let [start, end] = [1,1];
    
    while(end <= n && start <= end) {
        const sum = getSum(start, end, arr);
        if(sum === n) answer++;
        if(sum >= n) start++;
        if(sum < n) end++;
    }
    
    return answer;
}

function getSum(start, end, arr) {
    return (arr[start] + arr[end]) * (end - start + 1) / 2;
}

투 포인터를 이용하면 n = 10 일 때 다음과 같은 과정을 거치며 답을 찾는다.

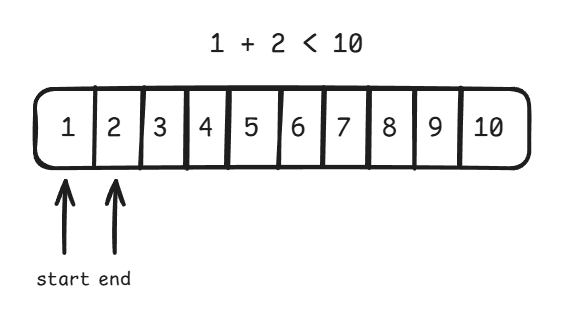
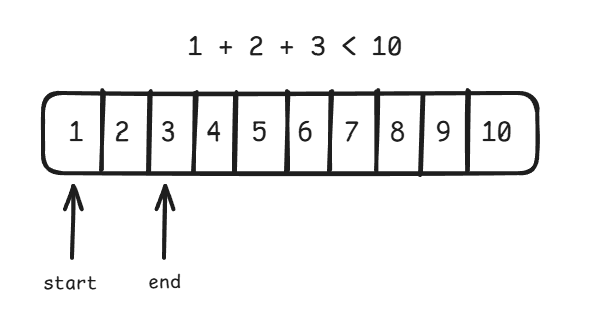
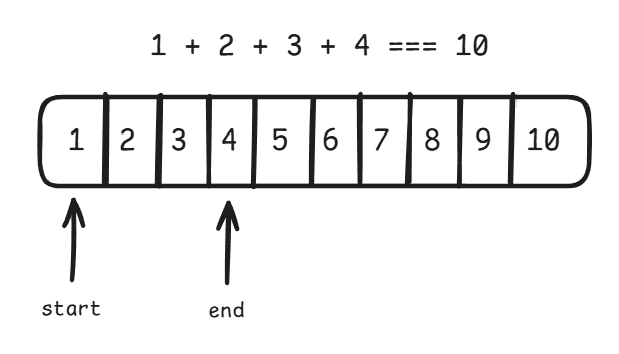
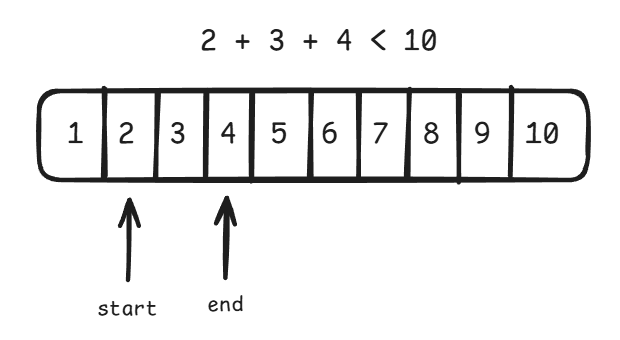
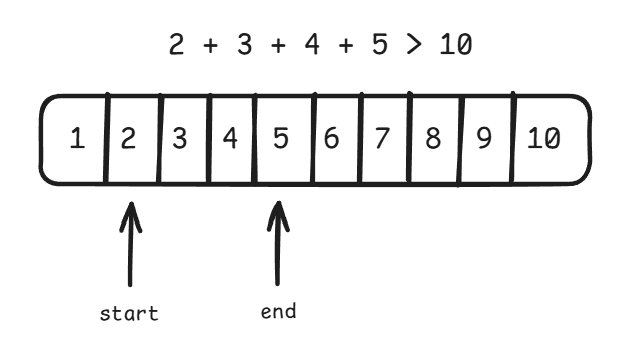
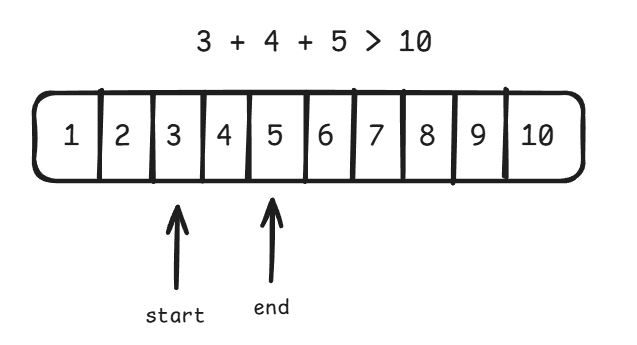
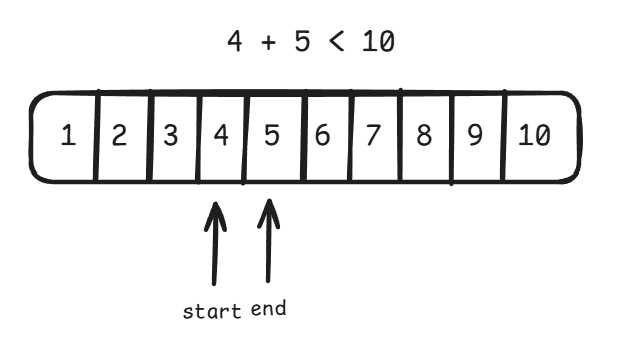
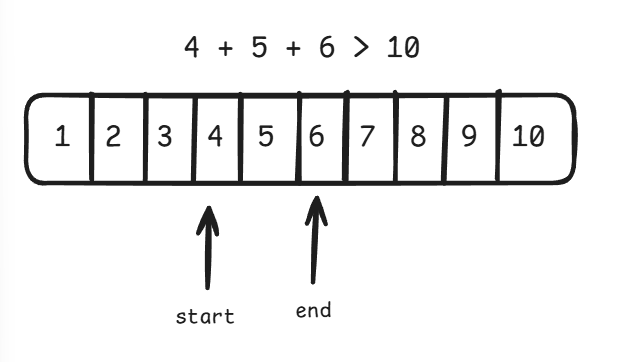
이때 start 부터 end 까지의 합을 구할 때, 단순히 start 부터 end 까지 순회하며 합을 누적해주는 방식이 아니라, 등차수열의 합을 구하는 공식을 이용하면 계산 한 번으로 합을 구할 수 있다.

\sum\limits_{n=start}^{end} a_n = \frac{(a_{start} + a_{end})\times(end-start+1)}{2}

이상한 현상 발생

원본 코드에서 answer 변수의 키워드를 var 에서 let 으로 수정했더니 갑자기 효율성 테스트에서 시간초과가 발생했다.

원본 코드

function solution(n) {
    var answer = 0;
    const arr = Array.from({length: n+1}, (_, i) => i);
    let [start, end] = [1,1];
    
    while(end <= n && start <= end) {
        const sum = getSum(start, end, arr);
        if(sum === n) answer++;
        if(sum >= n) start++;
        if(sum < n) end++;
    }
    
    return answer;
}

function getSum(start, end, arr) {
    return (arr[start] + arr[end]) * (end - start + 1) / 2;
}

수정 코드

function solution(n) {
    let answer = 0; // var를 let으로 수정함
    const arr = Array.from({length: n+1}, (_, i) => i);
    let [start, end] = [1,1];
    
    while(end <= n && start <= end) {
        const sum = getSum(start, end, arr);
        if(sum === n) answer++;
        if(sum >= n) start++;
        if(sum < n) end++;
    }
    
    return answer;
}

function getSum(start, end, arr) {
    return (arr[start] + arr[end]) * (end - start + 1) / 2;
}

원본 코드 점수: 100/100
수정 코드 점수: 83.3/100 (효율성 테스트 2,4,5,6 에서 시간초과 발생함)

vscode 에서 테스트해보니 실제로 let 키워드를 사용한 코드의 실행속도가 느렸다.

var 키워드를 사용한 코드

function solution(n) {
    var answer = 0;
    const arr = Array.from({ length: n + 1 }, (_, i) => i);
    let [start, end] = [1, 1];

    while (end <= n && start <= end) {
        const sum = getSum(start, end, arr);
        if (sum === n) answer++;
        if (sum >= n) start++;
        if (sum < n) end++;
    }

    return answer;
}

console.time("solution");
solutionB(10000);
console.timeEnd("solution");

// solution: 3.537ms

let 키워드를 사용한 코드

function solution(n) {
    let answer = 0;
    const arr = Array.from({ length: n + 1 }, (_, i) => i);
    let [start, end] = [1, 1];

    while (end <= n && start <= end) {
        const sum = getSum(start, end, arr);
        if (sum === n) answer++;
        if (sum >= n) start++;
        if (sum < n) end++;
    }

    return answer;
}

console.time("solution");
solutionB(10000);
console.timeEnd("solution");

// solution: 6.6ms

위 코드에서는 실행 속도가 약 2배 가량 차이가 나지만 n 을 키우면 키울수록 let 키워드를 사용한 코드의 실행 속도가 확연히 느려졌다.

n = 100,000으로 테스트해본 결과

var : 1.81ms

let : 12.173ms

이런 차이가 발생하는 원인은 간단히 말하자면 let 키워드를 사용했을 때 var 키워드를 사용했을 때보다 내부적으로 관리해줄 부분이 많아서 추가 비용이 발생하기 때문에 let 이 더 느린것이다. (자세한 내용은 추후 포스팅할 예정)

var 키워드를 사용해서 통과가 됐으니 그냥 내버려둘 수도 있지만 변수 키워드를 변경했다고 효율성 테스트에서 시간초과가 떴으니 로직 자체를 수정할 필요가 있어보인다.

수학적인 접근법 1

function solution(n) {
    let answer = 0;

    for (let k = 1; k <= n; k++) {
        if (n % k === 0 && k % 2 === 1) {
            answer++;
        }
    }

    return answer;
}

연속된 자연수의 합이 n이 되는 경우를 찾는 것이기 때문에 n이 주어졌을 때, 이를 연속된 자연수로 표현할 수 있는지 확인하면 된다.

n=15일 때, 연속된 수의 합이 15가 되는 경우는 다음과 같은 경우가 있다.

$1 + 2 + 3 + 4 + 5 = 15$
$4 + 5 + 6 = 15$
$7 + 8 = 15$
$15 = 15$

여기서 수열의 가운데 있는 수를 x 로 놓으면 식을 다음과 같이 변경할 수 있다.

$(x-2) + (x-1) + x + (x+1) + (x+2) = 15$
$(x-1) + x + (x+1) = 15$
$x + (x+1) = 15$
$x = 15$

수열의 중간 값인 x를 기준으로 왼쪽은 -1 씩 증가하고 있고, 오른쪽은 +1씩 증가하고 있다. 즉, 대칭을 이룬다. 따라서 식을 다음과 같이 수정해줄 수 있다.

$x + x + x + x + x = 5x = 15$
$x + x + x = 3x = 15$
$x + (x+1) = 2x+1 = 15$
$x = 15$

x의 계수를 k라고 했을 때,
1. k가 홀수인 경우, 중앙값 x가 자연수가 됨
2. k가 짝수인 경우, 중앙값이 자연수가 아니게 됨

위 예시에서 k=2일 때, $2x+1 = n$ 형태로 변형됨.
즉, n-1이 2로 나누어 떨어져야 x가 자연수가 됨.
따라서 k가 짝수인 경우 n은 홀수이어야 함.

위 내용을 종합하면, k가 홀수일 때 항상 x가 자연수가 되고, k가 짝수일 때는 n이 홀수라면 x가 자연수가 된다. 즉, n을 홀수 약수 k로 나눌 수 있는 경우가 우리가 찾는 답이다.

n의 모든 홀수 약수를 찾는다.
각 홀수 약수를 k로 놓고, x = n / k를 구한다.
x가 자연수면 유효한 해가 된다.

k가 2일 경우 n은 홀수여야 한다. n이 홀수인지 확인하는 과정은n의 홀수 약수를 구하는 과정에 포함되어있기 때문에 정확히 카운트된다.

수학적인 접근법 2

function solution(n) {
    let answer = 0;

    for (let k = 1; k <= Math.sqrt(n); k++) {
        if (n % k === 0) { // i가 n의 약수이고,
            if (k % 2 === 1) answer++; // 약수 i가 홀수라면 카운트 증가
            if ((n / k) % 2 === 1 && k !== Math.sqrt(n)) answer++; // n / i(다른 약수 쌍)도 홀수이면 카운트 증가(두 약수쌍이 동일할 때는 예외 ex. n=25 이고, i=5일때)
        }
    }

    return answer;
}

어떤 연속된 자연수 a 의 합이 n이라고 치자.
이때, 1씩 증가하는k개의 연속된 자연수의 합은 다음과 같이 표현할 수 있다.

n = a_1 + (a_1+1) +(a_1+2)+ ... +(a_1+k-1)

그리고 이를 등차수열의 합 공식으로 변형하면 다음과 같이 변형된다.

n=\frac{k(a_1+a_k)}{2} = \frac{k(a_1+a_1+k-1)}{2} = \frac{k(2a+k-1)}{2}

또한 우리는 연속된 자연수의 합을 구하고 있으므로 각각의 $a$ 는 자연수여야 한다.

$a$ 가 자연수가 되기 위한 조건은 위의 등차수열의 합을 이용해 다음과 같이 유도할 수 있다.

n = \frac{k(2a+k-1)}{2}

n \times 2 = k(2a+k-1)

\frac{n\times 2}{k} = 2a+k-1

\frac{n\times 2}{k} - (k-1) = 2a

\frac{\frac{2\times n}{k}}{2} - \frac{k-1}{2} = a

\frac{n}{k} - \frac{k-1}{2} = a

여기서 $a$ 가 자연수가 되려면

$\frac{n}{k}$ 와 $\frac{k-1}{2}$ 이 정수여야 한다.
$\frac{n}{k}$ 이 정수가 되려면 $n$ 은 $k$ 으로 나누어 떨어져야 한다. (= $k$ 는 $n$ 의 약수여야 한다.)
$\frac{k-1}{2}$ 이 정수가 되려면 $k-1$ 이 짝수가 되어야하므로 $k$ 는 홀수여야 한다.

따라서 n의 약수이면서 홀수인 k를 찾으면 된다.

또한 약수를 구할 때는 n의 제곱근까지만 확인해주면 되기 때문에 시간복잡도는 $O(\sqrt{n})$ 이다.

참고링크

잭슨

지속적인 성장

이전 포스트

[프로그래머스] 유전법칙 (JavaScript)

다음 포스트