[프로그래머스] 피보나치 수 (JavaScript)

문제

[프로그래머스] 피보나치 수

n이 주어졌을 때 n번째 피보나치 수를 1234567로 나눈 값을 구하는 문제다.

풀이

피보나치 수를 재귀적으로 구하는 과정은 다음과 같이 트리로 표현할 수 있다.

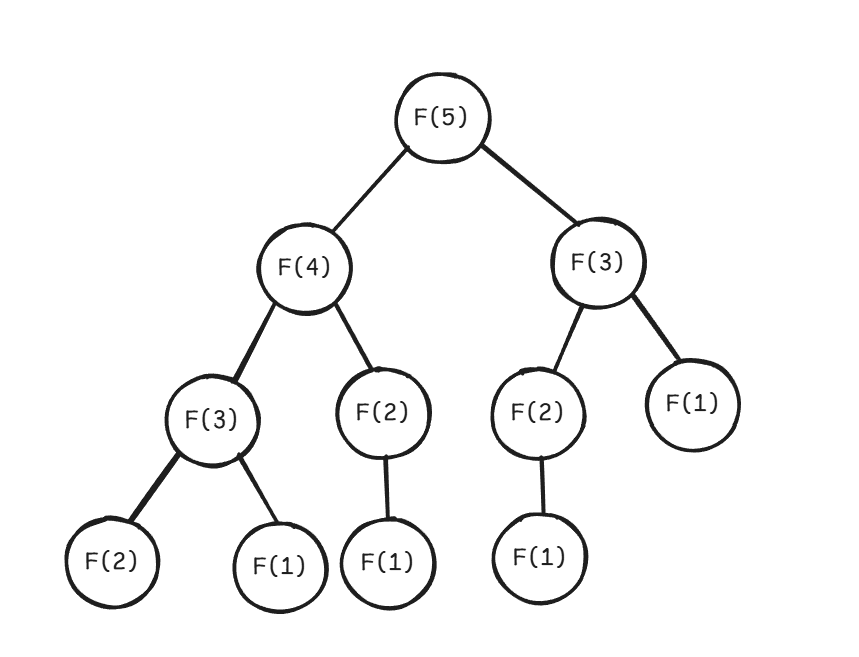
이 방법의 시간복잡도는 $O(2^n)$이다.

위 트리에서 보이다시피 중복된 계산을 반복해서 수행하는 모습이 보인다.
아래 그림에서 색칠된 부분이 중복된 부분이다.

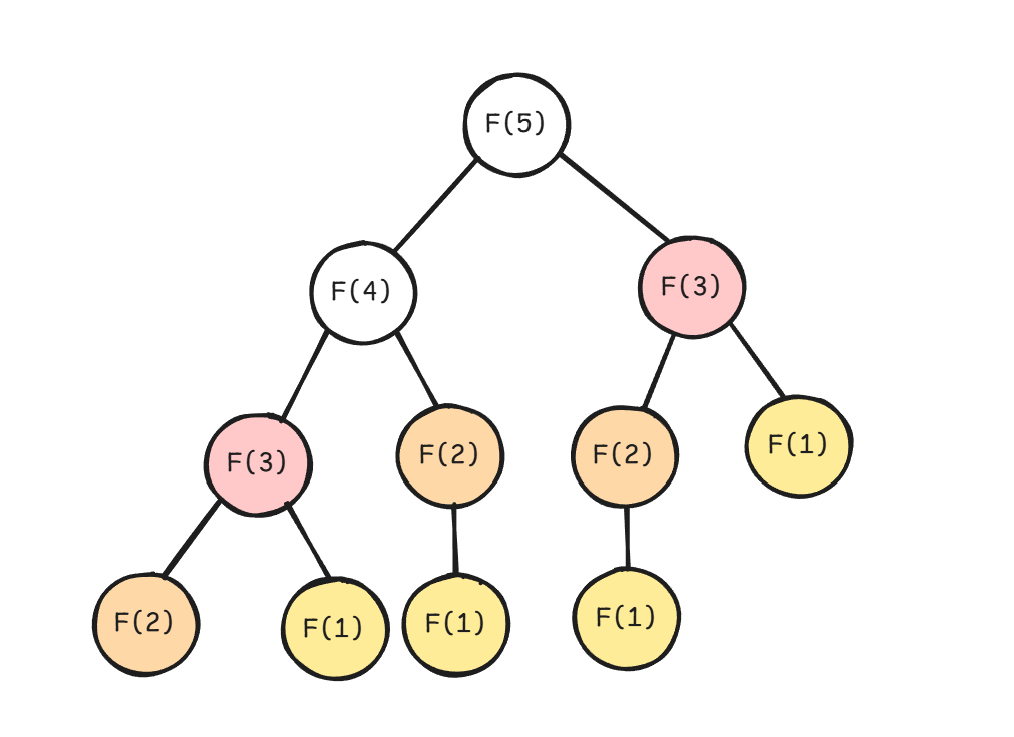
따라서 중복된 계산을 메모이제이션 하여 다음과 같이 동일한 연산을 만났을 때 이미 저장해둔 결과를 반환하면 된다.

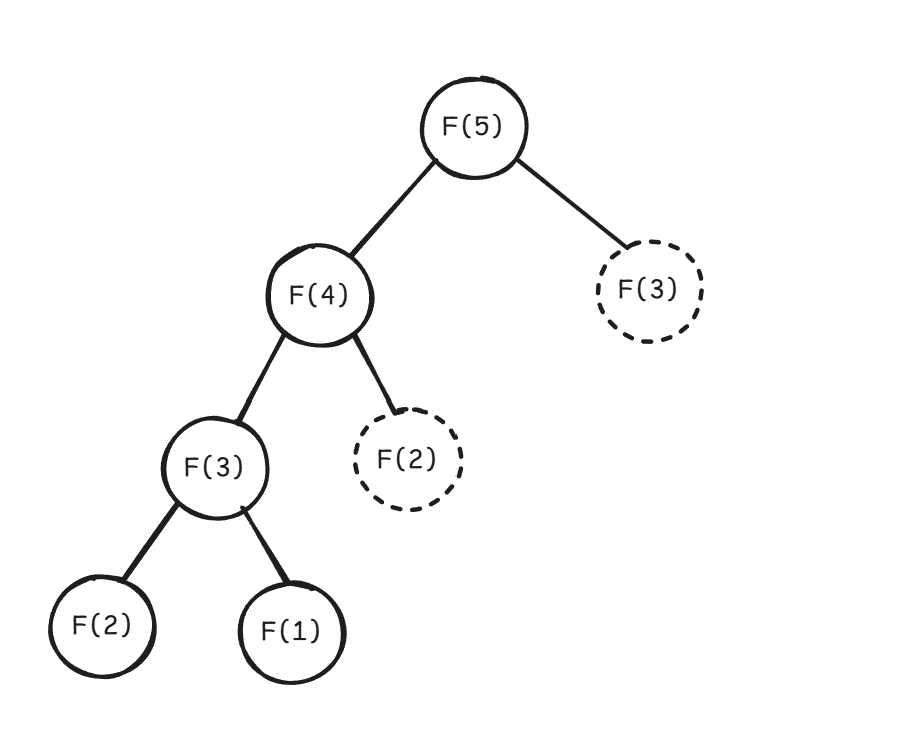
코드

function solution(n) {
    const arr = new Array(n + 1).fill(null);
    arr[0] = 0;
    arr[1] = 1;
    for(let i = 2; i <= n; i++) {
        arr[i] = (arr[i-1] + arr[i-2]) % 1234567;
    }
    
    return arr[n];
} 

처음엔 재귀함수로 구현했지만 n이 100,000이라 콜스택 깊이가 깊어져Maximum callstack error가 났다. 따라서 반복문을 통해 위와 같이 구현했다.

또한 처음에는 결괏값에만 1234567을 나눠서 반환했더니 계산과정에서 이미 Infinity가 되어 정확한 결과가 나오지 않았다. 따라서 반복문 안에서 매 계산마다 1234567을 나눠주도록 수정했다.