[BOJ 1932 정수삼각형]

정수삼각형

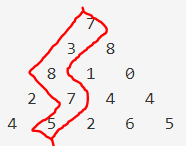
예시그림에서 최댓값은 7+3+8+7+5=30이다.

"아래층에 있는 수는 현재 층에서 선택된 수의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다."이므로 다음과 같이 재귀관계를 작성할 수 있다.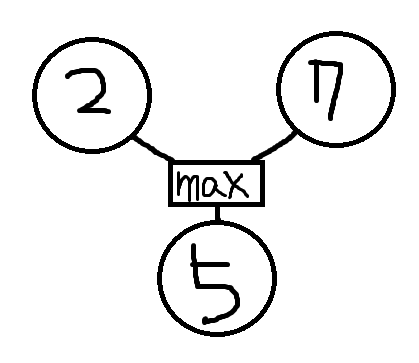
아래의 합은 원래수+max(대각선 왼쪽, 대각선 오른쪽)이다.
그리고 맨 왼쪽, 오른쪽은 대각선 숫자가 하나밖에 없으므로 누적합을 해주면 된다.
완성된 삼각형의 합은 다음과 같다.

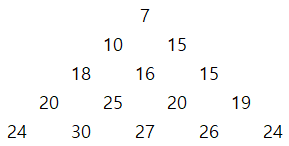
삼각형의 맨 아랫줄의 최댓값이 우리가 구하는 답이다.

// 데이터 입력 생략
// a[i][j]

// 시작점과 경계(왼쪽, 오른쪽 대각선) 작업
dp[1][1] = a[1][1];
for (int i = 2; i <= n; i++) {
	dp[i][1] = dp[i - 1][1] + a[i][1];
	dp[i][i] = dp[i - 1][i - 1] + a[i][i];
}

// 재귀식을 이용하여 dp계산
for (int i = 3; i <= n; i++) {
	for (int j = 2; j < i; j++) {
		dp[i][j] = a[i][j] + max(dp[i - 1][j - 1], dp[i - 1][j]);
	}
}

// 최댓값 찾기
int ans = -1;
for (int i = 1; i <= n; i++) {
	ans = max(ans, dp[n][i]);   // #include <algorithm>
}
printf("%d", ans);

사실 a[i][j]와 dp[i][j]를 구분하지 않고 하나의 dp[i][j]로 다 해결할 수 있다. 윗행의 결과값이 더이상 바뀌지 않기 때문이다.
아래 파이썬 코드는 그렇게 짠것이다.

N = int(input())

# 2차원 배열로 입력받기
dp = [list(map(int, input().split())) for _ in range(N)]

# 재귀식을 이용하여 dp[][] 계산하기
for i in range(1, N):
    for j in range(i+1):
        if j == 0:
            dp[i][j] += dp[i-1][j]
        elif 0 < j < i:
            dp[i][j] += max(dp[i-1][j-1], dp[i-1][j])
        else:
            dp[i][j] += dp[i-1][j-1]

# 정답출력하기. dp[-1]은 마지막 행(1차원 배열)이다.
print(max(dp[-1]))