[Codility] 10.2 Flags

Flags 문제 링크

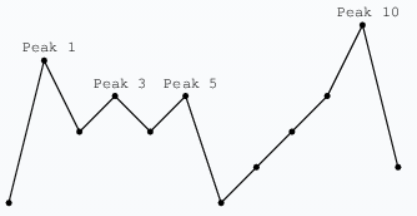
$K$개의 flag가 있다면, 각 flag의 거리는 $K$이상이여야 한다.
flag는 peak에만 꽂을 수 있을 때, 꽂을 수 있는 flag의 최대 개수는?

처음에 이분탐색의 upper_bound 방식으로 해결하려 했으나, flag와 distance가 서로 변화해서 잘 동작하지 않았다. (80%의 점수를 받았고, 매번 예외처리가 일정하지 않아서 옳지 않은 방법인 것 같다.)
이 문제를 푸는데 하루 이상 걸렸다.

구글링을 통해 얻은 지식은 다음과 같다.

1. $N$개의 지점에 대해, 거리가 $x$가 되도록 균일하게 놓을 수 있는 flag의 개수는 $\frac{N}{x} + 1$을 넘을 수 없다.
2. 즉, 매 거리 $i$마다, $i(i-1) \leq N$만큼만 반복하면 된다.

next[x]는 index가 x인 지점에 대해, 다음 peak의 index를 알려주는 데이터다.
매 거리마다 깃발을 놓을 수 있는 다음 peak의 index는 next[x+i]를 하면 알 수 있다. 그리고 별도의 반복문없이 $O(1)$마다 다음 peak을 알 수 있다는 것이 장점이다. (next[]를 만드는 것은 $O(n)$이다)

def solution(A):
    # peak들의 집합
    peak = set()
    for i in range(1, len(A) - 1):
        if A[i] > A[i - 1] and A[i] > A[i + 1]:
            peak.add(i)
    
    # 애초에 peak이 없거나 1개라면
    if len(peak) == 0 or len(peak) == 1:
        return len(peak)
    
    # preprocessing making next[]
    # next[x] : next peak index of x
    next = [0] * len(A)
    next[-1] = -1
    for i in range(len(A) - 2, -1, -1):
        if i in peak:
            next[i] = i
        else:
            next[i] = next[i + 1]
    
    i = 1
    max_flags = 0
    while i * (i - 1) <= len(A):
        idx = 0
        flags = 0
        while idx < len(A) and flags < i:
            idx = next[idx]
            if idx == -1:
                break
            idx += i # get next peak index where distance >= i
            flags += 1
        max_flags = max(max_flags, flags)
        i += 1
    
    return max_flags

시간복잡도는 $O(n + n + 1+2+3+...\sqrt{n}) = O(n)$이다. ($n$ = len(A))