Codility

MaxCounters문제 3줄 요약1\. N개의 counter가 있고, 배열 A에는 연산이 순차적으로 들어있다.2\. 연산1: Ai == N+1일때, 모든 counter를 counter의 최댓값으로 setting.2\. 연산2: Ai == X일때, X번째 counter

길이가 N인 수열에서, N/2개가 넘는 수가 똑같은 값인 원소가 존재할 때, 그 값을 leader of sequence 또는 leader라 한다.예1) 6, 8, 4, 6, 8, 6, 6의 경우, leader = 6이다. (그림)예2) 1, 2, 3, 4, 5, 6,

The dominator of array A is the value that occurs in more than half of the elements of A.leader를 구하는 것과 동일한 방식으로 접근하면 된다.스택에 숫자를 넣는다.1.1 스택의 top과 넣으려는

8.2 EquiLeader두 개의 구간으로 나누었을 때, 두 구간의 leader가 같은 경우의 수를 구하는 문제이다.이때 leader의 정의는 전에 다룬 정의와 동일하다The leader of this array is the value that occurs in mor

$n$개의 수 $a0, a_1, ..., a{n-1}$에 대해 가장 큰 부분합을 구하는 문제에 대해 생각해보자.위 그림의 예시에서, 가장 큰 부분합은 색칠된 부분이고 그 합은 10이다.알고리즘 문제를 좀 풀어봤다면, 이 문제는 dp로 해결할 수 있고 그 시간복잡도는 $

MaxDoubleSliceSum배열 A에 대하여 triplet(X, Y, Z) = $\\sum{x+1}^{y-1}Ai+\\sum{y+1}^{z-1}Ai$이고, 2개의 부분합으로 이루어져있다. 따라서 좌, 우에 해당하는 부분합의 최댓값의 합이 답이 된다. 그렇다면 $y$

MaxProfit배열 A과, $0 \\leq P \\leq Q <N$에 대하여, AQ-AP가 0 이상이면 profit, 음수이면 loss이다. 직관적으로 가장 큰 수에서 가장 작은 수를 빼면 된다.반복문을 돌면서 가장 작은 수를 업데이트하고, 현재 수에서 뺀 값을

MaxSliceSumMaximum subarray, Maximum subsequence sum이라고 알려져있는 문제이다. 워낙 유명하니 반드시 익혀두자.재귀식 $Si = \\max(0, Si-1 + Ai)$을 이용하면 된다.하지만 이 재귀식은 답이 음수(모든 원소가 음

어떤 수 $n$의 divisor를 구해보자. brute-force한 방법으로 1부터 $n$까지 반복문을 돌릴 수 있다. 이때 시간복잡도는 $O(n)$이 된다.$n=36$인 경우를 생각해보자. $2 \\times 8 = 16$이므로 $17~35$의 수는 체크할 필요가 없

풀이는

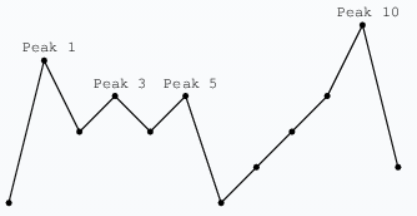
Flags 문제 링크$K$개의 flag가 있다면, 각 flag의 거리는 $K$이상이여야 한다.flag는 peak에만 꽂을 수 있을 때, 꽂을 수 있는 flag의 최대 개수는?처음에 이분탐색의 upper_bound 방식으로 해결하려 했으나, flag와 distance가

MinPerimeterRectangle 문제 풀기직사각형의 가로와 세로가 $A$, $B$라 하면, 이 직사각형의 둘레(perimeter)는 $2 \\times (A+B)$이다. 직사각형의 넓이가 $N$일 때, 직사각형의 둘레의 최솟값은? (단, 직사각형의 가로과 세로는

Peaks 문제 풀기문제를 간단히 요약하면 다음과 같다배열 A의 크기는 N이다0 < P < N - 1에 대하여 AP - 1 < AP and AP > AP + 1을 만족하면 P에서 peak라고 한다. (극대와 같은 개념)배열 A를 나누어서 부분배열의 원소

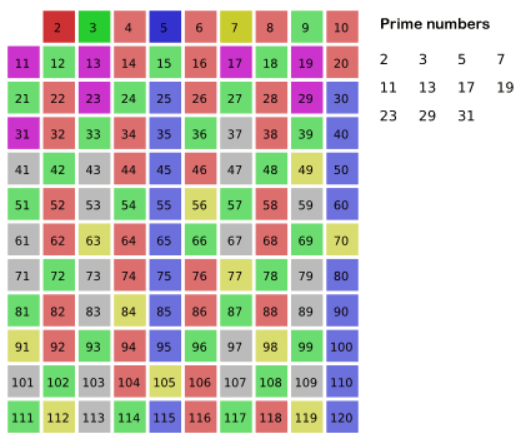
에라토스테네스의 체는 $n$ 이하의 수에서 소수를 찾는 테크닉이다.합성수 $n$에 대해 divisor는 최대 $\\sqrt{n}$ 이하에서만 존재한다. 이를 이용한 것이 에라토스테네스의 체이다.에라토스테네스의 체 - 위키피디아(https://ko.wikiped

CountNonDivisible 문제 풀기크기가 N인 배열 A가 주어진다.A의 원소들 중에서 A\[i]의 divisor가 아닌 것들의 개수를 리스트로 반환한다.2.1 즉, A의 원소들 중에서A\[i]의 약수를 제외한 것의 개수를 구한다(중복 허용)어떤 수의 diviso

semiprime(반소수)는 두 소수의 곱으로 이루어진 수이다.구간 \[Pk, Qk]에 존재하는 semiprime의 개수를 반환한다문제 접근방법은 다음과 같다prime을 구한 후, semiprime을 구한다semiprime의 개수를 구하는 query를 $O(1)$로 해

$0$이 아닌 두 정수 $a, b$가 $a=bq+c$가 성립한다고 하자.($q, c$는 정수)$a, b$의 공약수 전체집합과 $b,c$의 공약수 전체 집합은 서로 같다.특히 $(a, b)=(b,c)$이다.유클리드 호제법을 영어로 Euclidean Algorithm이라

ChocolatesByNumbers 문제 풀기원형으로 만들어진 초콜릿 조각 $N$개를 $M$의 간격으로 먹을 때, 먹을 수 있는 초콜릿 조각의 개수는? 단, 먹었던 조각으로 오면 멈춘다.초콜릿 조각의 위치는 $0 \\leq x \\leq N-1$이고, 현재 조각의 위치

CommonPrimeDivisors 문제 풀기$gcd(x, y)=1$이면 ($x, y$가 서로소라면) 공유하는 소수(소인수)가 없다는 뜻이다.$g = gcd(x, y)$라 하자. $gcd(x, g)=1$이라면 $x, y$사이에 공유하지 않는 소수가 존재한다는 뜻이므로

피보나치수열은 다음과 같은 점화식 구조를 갖는다$Fn\\begin{cases} 0 \\quad (n = 0)\\ 1 \\quad (n=1)\\ F{n-1} + F\_{n-2} \\quad(n \\ge 2)\\end{cases}$앞의 두개의 합이 다음 항의 값이 되는 특

BFS를 이용하여 해결했다. 현재 위치에서 피보나치 수열을 더하면서 다음 위치에 나뭇잎이 있으면 queue에 넣는다. 만약 다음 위치가 도착지라면 반복문을 중단한다.

Ladder 문제 풀기$K$번째 사다리에 오는 방법의 수는 $K-1 \\, , K-2$번째 사다리에서 오는 방법밖에 없다. $K$번째 사다리에 오는 방법의 수를 $ak$라 하면 $a_k=a{k-1}+a\_{k-2}$이므로 피보나치 수열 그 자체다. 하지만 초기값 $a_