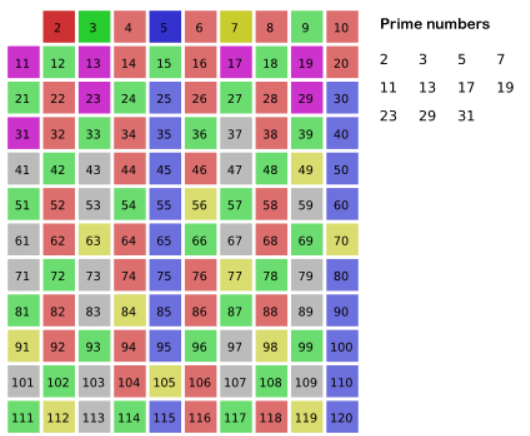
1. 에라토스테네스의 체

에라토스테네스의 체는 $n$ 이하의 수에서 소수를 찾는 테크닉이다.
1) 1은 소수가 아니므로 먼저 제외한다.
2) 2는 소수이므로 2보다 큰 2의 배수를 제외한다.
3) 3은 소수이므로 3보다 큰 3의 배수를 제외한다.
4) 4는 2)에서 제외되었다.
5) 5는 소수이므로 5보다 큰 5의 배수를 제외한다.
6) 은 2)에서 제외되었다.
...
이런식으로 나아가 $n$이하에서 소수를 찾는 방법이 에라토스테네스의 체이다.

에라토스테네스의 체 - 위키피디아

알고리즘 코드

아래는 내가 자주 사용하는 에라토스테네스의 체 코드다.
위키피디아와 codility를 섞어 작성했다.

# isPrime[x] : x가 소수라면 True, 소수가 아니라면 False
isPrime = [True] * (n + 1)

# 0과 1은 소수가 아니다
isPrime[0] = isPrime[1] = False


m = int(n ** 0.5) + 1
for i in range(2, m):
    if isPrime[i]:
        for j in range(i * i, n + 1, i):
            isPrime[j] = False

# 이후로 isPrime[x] 사용 가능

시간복잡도

매 소수 $p$에 대하여 $p < \sqrt{n}$이다. 따라서
$\frac{n}{2} + \frac{n}{3} + \frac{n}{5} + ... = n\sum\frac{1}{p_{i}}$
여기에 따르면 $\sum\frac{1}{p_{i}} \geq \log\log{n+1} - \log{\frac{\pi^2}{6}}$이므로 에라토스테네스의 체 알고리즘의 시간복잡도는 $O(n\log\log{n})$이다.

2. 소인수분해

산술의 기본정리(fundamental theorem of arithmetic)

$n$이 $1$보다 큰 정수일 때, $n$은 서로 다른 소수 $p_i$가 $k_i$번 곱해진 형태로 나타낼 수 있고 이를 나타내면 $n = p_{1}^{k_{1}}p_{2}^{k_{2}}...p_{t}^{k_{t}}$의 형태로 표시된다. $p_{i}^{k_{i}}$의 순서를 무시하면 유일하고 이를 표준분해(standard decomposition)라고 하고 이때 $p_i$는 $n$의 소인수(prime factor)라 한다.

소인수분해 알고리즘

먼저 어떤 수 $x$의 최소 divisor를 구한다. 이를 F[x]라 하자. 예를 들면 F[100] = 2, F[27] = 3, F[17] = 0이다.
에라토스테네스의 체를 응용하여 구할 수 있다.

def getMinFactor(n):
    F = [0] * (n + 1)
    m = int(n ** 0.5) + 1
    for i in range(2, m):
        if F[i] == 0:
            for j in range(i * i, n + 1, i):
                if F[j] == 0:
                    F[j] = i
    return F

소인수 분해는 F[x]를 이용해서 빠르게 구할 수 있다.
만약 F[x]가 양수라면(x가 합성수라면), F[x]도 소인수이므로 소인수 리스트에 추가하고, 원래 수 x에서 제거한다. (x //= F[x])
만약 F[x]가 0이라면 x는 소수이므로 바로 소인수 리스트에 추가하고 소인수분해를 종료한다.

def factorization(x, F):
    # 소인수들을 저장할 빈 리스트 생성
    primeFactors = []
    
    # 현재의 x가 합성수일때
    while F[x] > 0:
        primeFactors += [F[x]]
        x //= F[x]
      
    # 현재의 x는 소수이다
    primeFactors += [x]
    
    # 소인수가 오름차순으로 리스트에 정렬되어있다.
    return primeFactors

시간복잡도

getMinFactor의 시간복잡도는 에라토스테네스의 체와 같다.($O(n \log \log{n})$)
factorization(x, F)의 시간복잡도는 $O(\log{x})$이다.

3. 예제

[BOJ 16563 어려운 소인수분해]

def factorization(x, F):
    while F[x] > 0:
        print(F[x], end=' ')
        x //= F[x]
    print(x)
    return

import sys

N = int(input())
L = list(map(int, sys.stdin.readline().split()))
F = [0] * (5000001)
m = int(5000001 ** 0.5) + 1
for i in range(2, m):
    if F[i] == 0:
        for j in range(i * i, 5000001, i):
            if F[j] == 0:
                F[j] = i

for x in L:
    factorization(x, F)