[Codility] 4.2 MaxCounters

MaxCounters

문제 3줄 요약
1. N개의 counter가 있고, 배열 A에는 연산이 순차적으로 들어있다.
2. 연산1: A[i] == N+1일때, 모든 counter를 counter의 최댓값으로 setting.
2. 연산2: A[i] == X일때, X번째 counter를 1 증가한다.(단, 1<=X<=N)

codility 문제는 쉬우면서 어렵다
100%를 맞추려면 거의 O(n)안에 구현해야한다.

# NAIVE code (77%~88% score)
def solution(N, A):
    L = [0] * N
    cur_max = 0
    for x in A:
    	# setting cur_max for all counters
        if x == N + 1:
            for i in range(N):
                L[i] = cur_max
        
        # increasing each counter
        else:
            L[x - 1] += 1
            # resetting cur_max
            cur_max = max(cur_max, L[x - 1])

    return L

순진하게(?) 하라는대로 짜면 (연산1)에서 O(N)의 시간복잡도를 잡아먹으므로 전체적으로 O(MN)이 되어 performance에서 좋은 점수를 얻을 수 없다. 그렇다면 (연산1)의 특징을 이용하면 시간을 대폭 줄일 수 있다.

A[i] == N + 1일때마다 매번 해야할까?
미리 변수를 추가해서 해결할 수 있지 않을까?

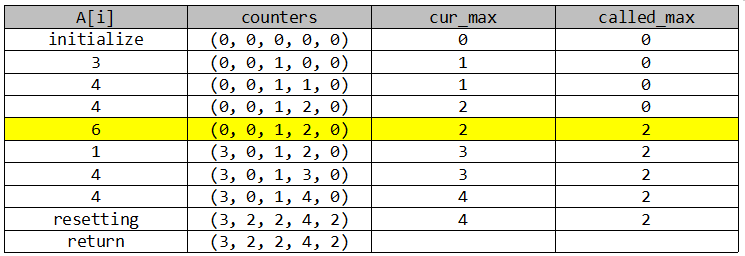
노랗게 색칠한 부분이 A[i] == N+1일때(i=3)이다. 이때 모든 counter를 resetting하지 않고 called_max = cur_max로 저장한다. 그리고 그 이후 counter를 증가시킬때마다 called_max + 1(i=4일때)인지, 아니면 원래 값을 증가시킬지만(i=6) branch를 나누면 된다.
그리고 맨 나중에는 called_max보다 작은 값들을 called_max로 바꿔주면 된다. 한번도 counter가 증가하지 않았다면 다같이 최댓값으로 저장될때만 값이 바뀌었기 때문이다.

# 100% score
def solution(N, A):
    L = [0] * N
    cur_max = 0
    called_max = 0

    for x in A:
        # resetting called_max
        if x == N + 1:
            called_max = cur_max
        else:
            # increasing counter
            if L[x - 1] < called_max:
                L[x - 1] = called_max + 1
            else:
                L[x - 1] += 1
            
            # resetting cur_max
            if L[x - 1] > cur_max:
                cur_max = L[x - 1]
    
    # resetting All data in L
    for i in range(N):
        if L[i] < called_max:
            L[i] = called_max
    
    return L

codilty는 어지간하면 O(N)으로 다 해결할 수 있다.