[Codility] 9.1 MaxDoubleSliceSum

MaxDoubleSliceSum
배열 A에 대하여

이고, 2개의 부분합으로 이루어져있다. 따라서 좌, 우에 해당하는 부분합의 최댓값의 합이 답이 된다. 그렇다면 $y$의 인덱스를 중심으로 부분합을 구한다. $S_1, S_2$를 다음과 같이 정의하자.

$S_1$는 $1 \le i < N-1$, $S_2$는 $N-1 \ge i >= 1$로 인덱스를 옮기면서 최대부분합을 구한다. 재귀식은 다음과 같다.

# initiate S1, S2
S2[i] = [0, 0, ..., 0]
S2[i] = [0, 0, ..., 0]

# 양끝점은 부분합에 계산하지 않는다. A[X], A[Z]는 제외되기 때문
S1[i] = max(0, S1[i - 1] + A[i]) for i in 1, 2, ..., N-2
S2[i] = max(0, S2[i + 1] + A[i]) for i in N-2, N-1, ..., 1

S[i] = S1[i - 1] + S2[i + 1]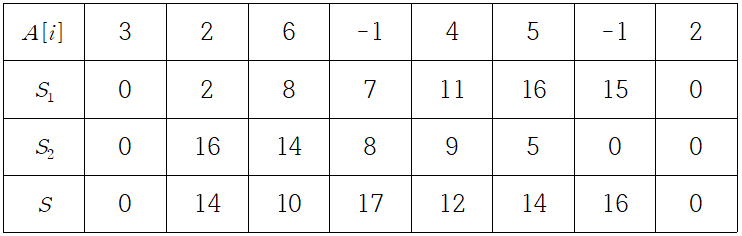

max()안에 0과 비교하는 것은 X, Y가 인접한 경우, Y, Z가 인접한 경우에는 부분합이 0이기 때문이다.

정답코드는 다음과 같다.

def solution(A):

    N = len(A)
    if N == 3:
      return 0
      
    # initialize S1, S2
    S1 = [0] * N
    S2 = [0] * N

    # Construct S1
    for i in range(1, N - 1):
        S1[i] = max(0, S1[i-1] + A[i])
    
    # Construct S2
    for i in range(N-2, 1, -1):
        S2[i] = max(0, S2[i+1] + A[i])

    # Calculate S
    S = 0
    for i in range(1, N-1):
        S = max(S, S1[i-1] + S2[i+1])

    return S