이진 탐색 트리들

Gunjoo Ahn·2022년 8월 14일

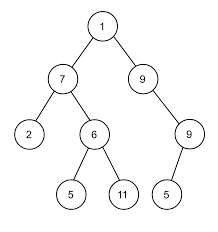
이진 트리

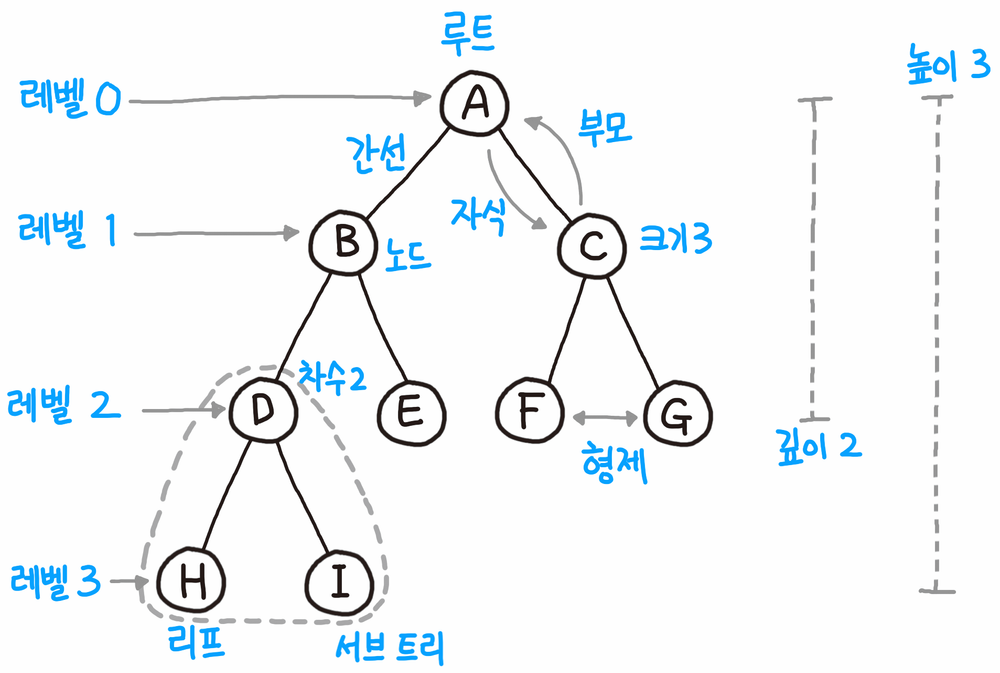
위 그림 처럼 노드에 자식들의 수가 2이하인 트리가 이진 트리이다.

이진 탐색 트리(Binary Search Tree)

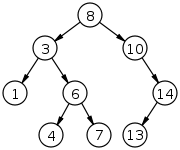
값을 저장할 때, 노드보다 값이 작으면 왼쪽 자식으로 보내고 크면 오른쪽 자식으로 보낸다. 리프에 도달하면 노드를 생성하여 값을 저장한다. 이렇게 생성된 트리가 이진 탐색 트리이다. 트리인 만큼 검색, 삽입, 삭제가 모두 평균 O(log n) 이다.

문제는 순차적으로 커지거나 작아지는 숫자 시퀀스를 삽입했을 때, 연결 리스트랑 동일하다는 것이다. 계속 오른쪽이나 왼쪽 자식에다가 값을 넣는 것. 그래서 최악의 경우, 모든 트리 operation의 시간 복잡도가 O(n)이 된다. 그래서 self-balancing 트리들이 나오게 된다.

Algorithm	Average	Worst case
Space	O(n)	O(n)
Search	O(log n)	O(n)
Insert	O(log n)	O(n)
Delete	O(log n)	O(n)

AVL 트리(Adelson-Velsky and Landis Tree)

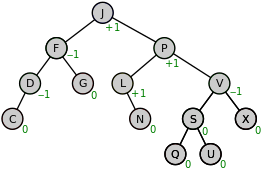
AVL 트리는 self-balancing 트리중 하나이다. 이 트리는 삽입 후, 노드 양쪽에 리프 노드까지의 거리의 차가 2이상인 것을 허용하지 않는 것이다. 만약 2이상일 경우 밸런싱을 한다. 밸런싱은 차이나는 노드를 기준으로 오른쪽이나 왼쪽으로 회전시키는 방식이다.

Algorithm	Average	Worst case
Space	Θ(n)	O(n)
Search	Θ(log n)	O(log n)
Insert	Θ(log n)	O(log n)
Delete	Θ(log n)	O(log n)

레드-블랙 트리(Red-Black Tree)

레드 블랙 트리도 self-balancing 트리중 하나이다. 노드에 빨간색, 검정색을 depth에 따라 번갈아 가면서 칠하는 규칙을 만들어 트리 밸런싱을 유지하는 트리이다. 밸런싱이 유지되는 규칙은 아래와 같다.

노드는 레드 혹은 블랙이다.
루트 노드는 블랙이다.
모든 리프 노드들(NIL)은 블랙이다.
레드 노드의 자식 노드들은 모두 블랙이다. 즉 레드 노드는 연속될 수 없다.
어떤 노드로부터 시작되어 그에 속한 하위 리프 노드에 도달하는 모든 경로에는 리프 노드를 제외하면 모두 같은 개수의 블랙 노드가 있다

위 규칙을 만족시키기 위하여 단순히 색을 다시 칠하거나( Θ(1) ), 트리를 회전( O(log n) )하거나 한다.

Algorithm	Average	Worst case
Space	O(n)	O(n)
Search	Θ(log n)	O(log n)
Insert	Θ(log n) + Θ(1)	O(log n)
Delete	Θ(log n) + Θ(1)	O(log n)

탐색 시간으로 인해 삽입, 삭제의 경우 Θ(log n) 이상의 시간이 걸릴 수 밖에 없다. 다만 색만 칠하는 경우 Θ(1) 라는 것을 표현하고 싶어 삽입, 삭제에 따로 Θ(1) 를 넣었다.

AVL vs Red-Black

두 트리 모두 삽입, 삭제, 검색시 최악의 경우 O(log n) 의 시간이 소요되는 것은 같다. 다만 AVL 트리는 차이가 2이상이 나지 않게 한다는 제약 조건이 상당히 강력한 제약 조건이기에 거의 삽입 때마다 밸런싱이 이루어져 레드 블랙 트리보다 삽입 성능이 좋지 못한 편이다. 그렇지만 강력한 제약으로 인하여 검색 성능은 레드 블랙 트리보다 유리하다.

그 외(B, B+ Tree)

B Tree와 확장버전으로 B+ Tree도 검색 트리로서 많이 사용된다. 자식을 2개 이상 가질 수 있으며 밸런싱 트리중 하나이다. B+ Tree는 DB Indexing에 사용된다.

Amortized Analysis

최악의 경우 발생하는 시간 복잡도가 정말 가끔 일어나는데, 해당 알고리즘을 최악으로 표현하는 것 대신 평균으로 표현하기 위한 시간 복잡도 분석이다. O 대신 Θ로 표기한다.
유명한 예로 queue 삽입이 있다. 원소를 삽입하려는데 queue 공간이 전부 찼다면, 2배의 공간을 할당하고 기존 원소를 복사한다. 이 것으로 인하여 평소에는 O(1)이지만 최악의 경우 O(n)이 된다.

위 예제에 대하여 간단하게 amortized 시간 복잡도를 구해보자면, n + 1번의 작업들의 평균으로 구하는 것이다. n번의 Θ(1) 와 1번의 Θ(n)이 발생 했으므로

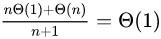
따라서 시간 복잡도는 Θ(1) 인 것이다.