Why

❓ 왜 Segment Tree를 사용할까?

구간 쿼리(합, 최댓값, 최솟값), 업데이트 작업의 효율화

What

📒 Segment Tree 특징

1. 구간 쿼리
O(log N)
특정 범위 [L,R]에 대한 값을 계산

2. 업데이트
O(log N)
특정 인덱스 i 값을 변경할 때, 해당 구간에 영향을 미치는 상위 노드들을 갱신

How

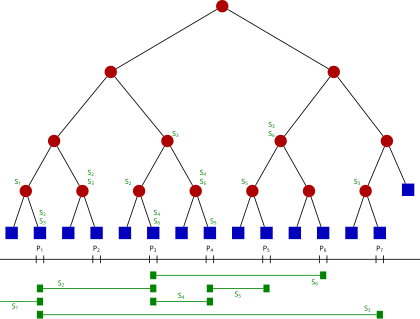
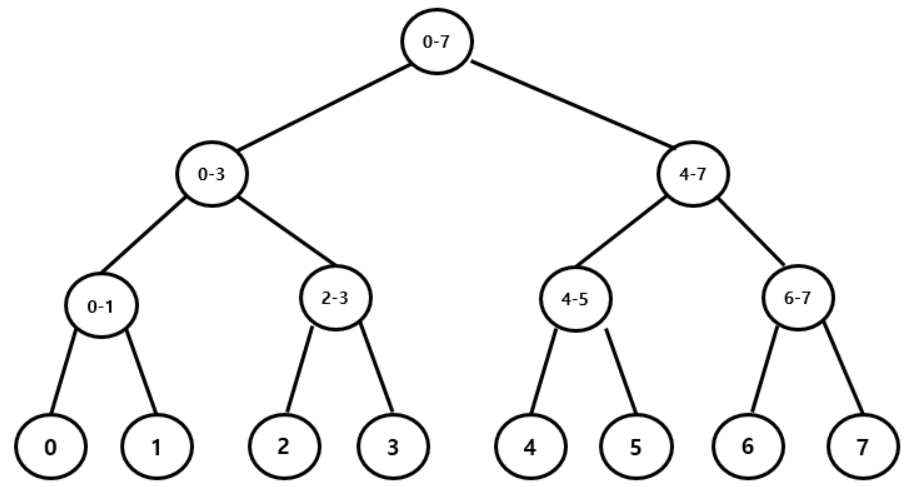
• 구간을 기준으로 이진 트리를 나눈다. ([0,n] → [0,n/2], [n/2+1, n/2] → ….)
• 가장 아래의 리프 노드들이 주어진 배열의 값들이다.
• 값 업데이트 시, 가장 아래의 리프 노드를 먼저 수정한 후, 부모 노드들을 갱신한다.
• 구간 쿼리 시 , 범위에 맞는 노드들만 찾아가며 구간 쿼리 수행한다.
• 트리의 크기의 경우, 딱 맞추려면 2*2^log(N) 이지만 넉넉히 4N 하면 된다.

#include <bits/stdc++.h>

using namespace std;

class SegmentTree {
private:
    vector<int> tree;
    vector<int> data;
    int size;

    // 세그먼트 트리 초기화
    int init(int node, int start, int end) {
        if (start == end) {
            // 리프 노드
            return tree[node] = data[start];
        }
        int mid = (start + end) / 2;
        return tree[node] = init(node * 2, start, mid) + init(node * 2 + 1, mid + 1, end);
    }

    // 구간 합 쿼리
    int query(int node, int start, int end, int left, int right) {
        if (right < start || left > end) {
            // 범위 밖
            return 0;
        }
        if (left <= start && end <= right) {
            // 범위 안
            return tree[node];
        }
        int mid = (start + end) / 2;
        return query(node * 2, start, mid, left, right) + query(node * 2 + 1, mid + 1, end, left, right);
    }

    // 값 갱신
    void update(int node, int start, int end, int index, int value) {
        if (index < start || index > end) {
            // 범위 밖
            return;
        }
        if (start == end) {
            // 리프 노드 갱신
            tree[node] = value;
            return;
        }
        int mid = (start + end) / 2;
        update(node * 2, start, mid, index, value);
        update(node * 2 + 1, mid + 1, end, index, value);
        tree[node] = tree[node * 2] + tree[node * 2 + 1];
    }

public:
    // 생성자
    SegmentTree(const vector<int>& input) {
        size = input.size();
        data = input;
        tree.resize(size * 4); // 트리 크기는 배열 크기의 약 4배
        init(1, 0, size - 1);
    }

    // 구간 합 쿼리 호출
    int query(int left, int right) {
        return query(1, 0, size - 1, left, right);
    }

    // 값 갱신 호출
    void update(int index, int value) {
        update(1, 0, size - 1, index, value);
    }
};

❓ Prefix Sum(누적합) 과의 차이점은?

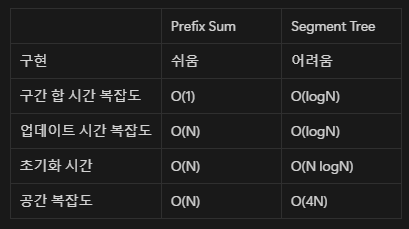
업데이트가 일어나는 경우 Segment Tree 사용
단순한 구간합만 구하는 경우 Prefix Sum 사용