Lazy Propagation은 Segmentg Tree의 응용 단계이다

Segmentg Tree에서 발생할 수 있는 단점을 해결하기 위해 사용하는 방법이므로, Segment Tree에 대해 알아야한다.

Segment Tree 링크

Why

❓ Lazy Propagation란?

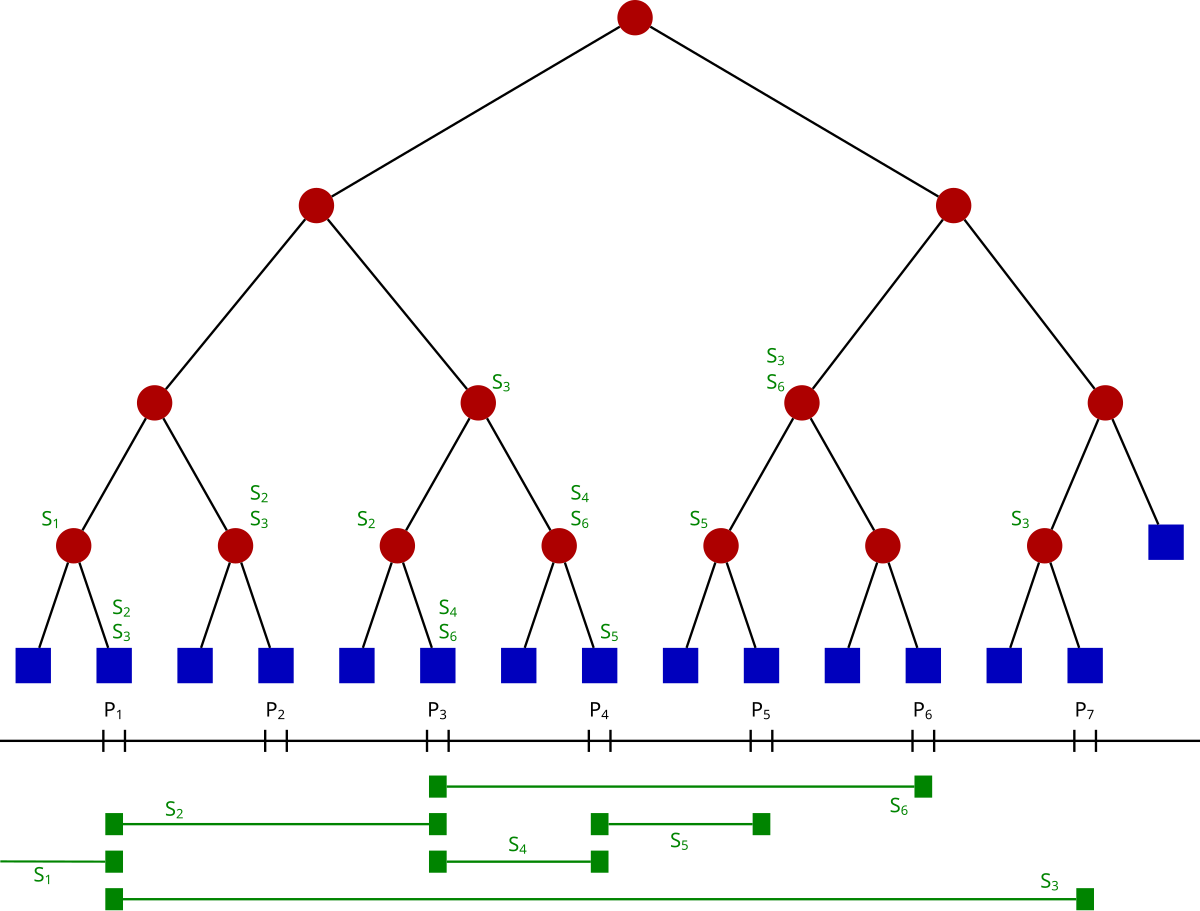
해당 값이 변경 되었을 때, 당장 업데이트하지 않고, 필요할 때 업데이트를 진행하는 방법

❓ 왜 Lazy Propagation을 사용할까?

Segment Tree : 구간에 대한 연산 처리에 유용

• Segment Tree의 경우
  특정 구간의 모든 값을 일괄적으로 변경 할 때
  a~b구간(구간 M)의 모든 값을 변경 할 때 O(M logN)의 시간 복잡도를 가진다.

• Lazy Propagation의 경우
  특정 구간을 쿼리 할 때, 업데이트를 하며 쿼리 값을 리턴하면 O(logN)의 시간 복잡도를 가진다.

What

📒 Lazy Propagation 특징

1. Lazy 배열
각 노드의 업데이트 정보를 저장하는 배열
특정 노드에 대해 처리되지 않은 업데이트 정보를 저장

2. 구간 쿼리
O(log N)
특정 범위 [L,R]에 대한 값을 계산

3. 구간 업데이트
O(log N)
특정 구간을 일괄적으로 업데이트 할 때

How

• a~b 구간을 모두 value(ex) +1) 업데이트 시
  1. a~b 구간에 완전히 포함
  2. a~b 구간에 부분만 포함
  3. a~b 구간에 포함되지 않음

1)의 경우 (end-start+1)*value로 Tree 업데이트 후 리프 노드들은 바로 업데이트 하지 않고 Lazy에 저장
2)의 경우 1)에서부터 업데이트 되며 자동으로 업데이트
3)의 경우 업데이트 할 필요 없음

결국, Lazy 하게 업데이트하는 것은 1)의 자식 노드들 이다.
1)의 자식 노드들이 쿼리를 받거나 업데이트를 하게 되면 그때 1)에서부터 Lazy에 저장해두었던 정보들이 Propagate 된다.

class SegmentTree{
private:
    vector<int> tree;
    vector<int> data;
    vector<int> lazy;
    int size;

    int init(int node, int start, int end){
        if(start == end)
            return tree[node]=data[start];

        int mid = (start + end)/2;
        return tree[node] = init(node*2, start, mid) + init(node*2 + 1, mid+1, end);
    }

    void propagate(int node, int start, int end){
        if(lazy[node]!=0){
            tree[node]+= (end-start+1)*lazy[node];

            if(start!=end){
                lazy[node*2]+=lazy[node];
                lazy[node*2+1]+=lazy[node];
            }

            lazy[node]=0;
        }
    }
    
    void updateRange(int node, int start, int end, int left, int right, int value){
        propagate(node, start, end);

        if(left > end || right < start)
            // 범위 밖
            return;

        if(left <= start && right >= end){
            // 범위 안
            tree[node]+=(end-start+1)*value;
            if(start!=end){
                lazy[node*2]+=value;
                lazy[node*2+1]+=value;
            }
            return;
        }

        int mid = (start + end)/2;
        updateRange(node*2, start, mid, left, right, value);
        updateRange(node*2+1, mid+1, end, left, right, value);
        tree[node]=tree[node*2]+tree[node*2 + 1];
    }

    int query(int node, int start, int end, int left, int right){
        propagate(node, start, end);

        if(left > end || right < start)
            return 0;

        if(left <= start && right >= end)
            return tree[node];

        int mid = (start + end)/2;
        return query(node*2, start, mid, left, right) + query(node*2+1, mid+1, end, left, right);
    }

public:
    SegmentTree(vector<int> input){
        size = input.size();
        data=input;
        tree.resize(size*4);
        lazy.resize(size*4);
        init(1, 0, size-1);
    }

    void updateRange(int left, int right, int value){
        updateRange(1, 0, size-1, left, right, value);
    }

    int query(int left, int right){ 
        return query(1, 0, size-1, left, right);
    }
};

❓ Segment Tree와의 차이점은?

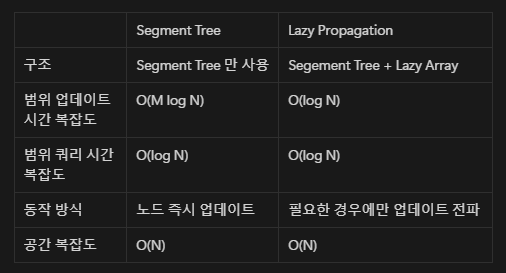
특정 인덱스에 대한 값 변경이 있는 경우 Segment Tree 사용
특정 구간에 대한 값 변경이 있는 경우 Lazy Propagation 사용