신경망(Neural Network)
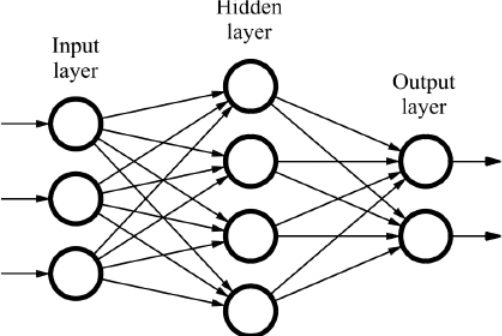
신경망을 그림으로 나타낸 것이다. 왼쪽부터 입력층(input layer), 은닉층(hidden layer), 출력층(output layer)이라고 부른다. 입력층과 출력층은 사람에게 보이지만, 은닉층은 보이지 않는다. 가중치를 갖는 층을 기준으로 2층 신경망이라고 부르겠다. 왼쪽부터 0층, 1층, 2층이 된다.
지난 번에 공부했던 퍼셉트론을 보겠다.

이 퍼셉트론을 수식으로 나타냈었는데, 그림에는 수식에 있는 편향 b가 표현되지 않는다. 따라서 이 퍼셉트론에 편향을 반영한다. 이렇게 되면 가중치가 b고 입력이 1인 뉴런이 추가되어 총 3개의 입력을 가진 퍼셉트론이 탄생한다. 편향의 입력 신호는 항상 1이다. 이를 y = h(x)로 표현하여 h(x)가 0보다 작거나 같을 때 0을 반환하고, 0보다 클 때 1을 반환하는 것으로 생각할 수 있다.
이 때 h(x)처럼 입력신호의 총합을 출력신호로 변환하는 함수를 활성화 함수(activation function)이라고 부른다.
📌활성화 함수
활성화 함수 중 어떠한 임계값을 경계로 출력이 바뀌는 함수를 계단 함수(step function)라고 한다. 지금까지 본 퍼셉트론에서의 활성화 함수가 바로 계단 함수이다. 계단함수 외에도 다양한 활성화 함수가 있다.
시그모이드 함수(sigmoid activation function)
신경망에서 자주 이용하는 활성화 함수이다.
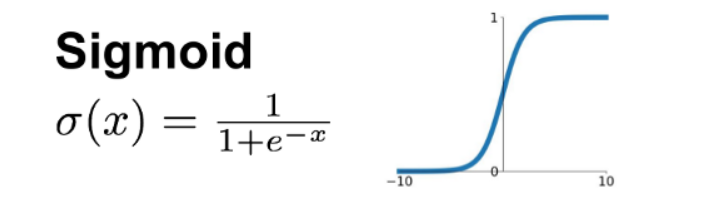
그래프의 모양이 계단함수와 매우 유사하다.
▼계단함수
하지만 계단 함수와는 달리 시그모이드 함수는 모든 구간에서 미분 가능하다. 계단 함수는 0 또는 1의 두 값 중 하나를 반환하지만, 시그모이드 함수는 0과 1사이의 연속적인 실수값을 반환한다. 두 함수 모두 0과 1 사이의 값만 출력할 수 있다는 공통점이 있다.
📌비선형 함수
두 함수 모두 비선형 함수이다. 바꿔 말하면 직선 1개로 그릴 수 없는 함수이다.
신경망에서는 비선형 함수를 활성화 함수로 사용해야 하는데, 선형 함수를 사용하면 함수를 여러번 합성하여도 결국 동일한 선형 함수가 나오기 때문에, 층을 쌓는 의미가 없어진다. 따라서 층을 쌓고 효과를 얻으려면 비선형함수를 사용해야 한다.
렐루 함수(ReLU function:Rectified Linear Unit)
시그모이드 함수와 같이 신경망에서 사용되는 활성화 함수이다. 입력이 0을 넘으면 입력을 그대로 출력하고, 0 이하에서는 0을 출력한다. 즉 0 이상이면 항등함수로 작용하고, 0보다 작은 경우에 모두 0을 출력하는 함수라고 할 수 있다.
0 미만에서는 학습하지 않고 활성화되지 않는다.
📌다차원 배열
신경망 구현시 다차원 배열의 계산이 중요하다. 파이썬 numpy배열을 사용하여 다차원 배열의 연산을 숙달하도록 한다.
(실습)
📌출력층 설계
신경망은 classification, regression에 모두 사용 가능하다. 하지만 출력층에서 사용하는 활성화 함수는 다르다. regression에는 항등함수를 사용하고, classification에는 소프트맥스 함수를 사용한다.
항등함수
회귀에 사용되며, 입력값이 그대로 출력되는 함수이다.
소프트맥스(softmax) 함수
분류에 사용되며, 분모는 모든 입력신호의 지수함수의 합이고 분자는 i번째 입력 신호의 지수함수이다.
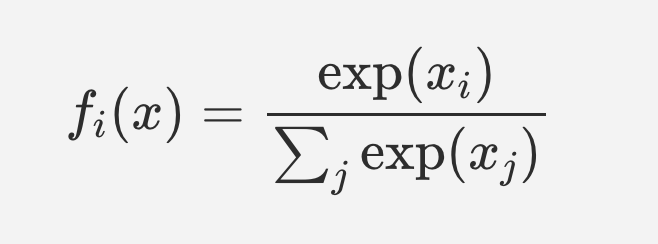
소프트맥스 함수 각각의 출력은 모든 입력 신호로부터 영향을 받는다.
소프트맥스 함수의 결과는 확률값이며, 확률이므로 총 합은 1이 된다. 이러한 특성을 이용하여 클래스에 속할 확률을 구하면 분류에 이용할 수 있다.
❗주의할 점
소프트맥스 함수는 지수함수를 계산하는 식이다. 지수함수는 지수에 따라 수가 너무 커질 수 있어 입력 신호 중 가장 큰 값을 빼주면 오류가 발생하지 않고 결과를 얻어낼 수 있다.
오늘은 신경망에 대해 공부해보았다.
사실 수식이나 실습 내용들도 첨부하여 게시하면 나중에 복습할 때 도움이 될 것 같은데, 아무래도 저작권에 대한 부분이 조심스럽다보니 실습은 스스로 해보고 끝내거나 이후 실습 내용을 살짝 변형하여 진행해보고 게시할 수도 있을 것이다.
수식이나 시각자료들을 때에 맞게 첨부하지 못하는 부분이 매우 아쉽다.