[AI스쿨 7기, 10주차] Ch2. 머신러닝 프로세스(데이터 용어, 준비 과정, 모델링) / Ch3. 모델링(KNN, Logistic Regression)

K-MOOC '실습으로 배우는 머신러닝' 김영훈 교수님

2-1. 머신러닝 프로세스 개요

• Business Understanding : Prior Knowledge, 도메인? & Data Understanding
• Prepare Data
• Model(with Training Data)
• Model 적용, evaluation(with Test Data)
• Deployment
• Knowledge and Actions

---

데이터 용어

• Dataset
• Data Point(Observation) : 관측치 / 1번 데이터, 2번 데이터
• Feature(Variable, Attribute) : 데이터 구성하는 특성. ex) 숫자형, 범주형, 시간, 텍스트, 이진형/ 키, 나이, 몸무게
• Label(Target, Response) : 궁극적으로 예측하고자 하는 변수
  ex) 키, 나이, 몸무게가 X / 혈압이 Y(Target)

---

분류, 회귀

---

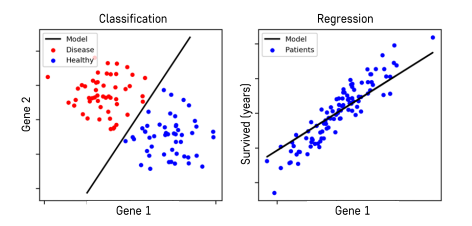
🔥Data 준비과정🔥

• Dataset Exploration(EDA) : 변수 특성 탬색
• Missing Value
• Data Types and Conversion : 숫자, 텍스트, 범주, 시간 등 분석 가능한 형태로 데이터 타입 변환
• Normalization : ex) 평균을 빼고, 표준편차로 나눠줌. X/(max-min)
• Outliers
• Feature Selection : 모델링에서 중요한 변수, 그렇지 않은 변수 선택
• Data Sampling : 데이터 일부분 추출하는 과정

모델링

• Build Model -> Evaluation 후 다시 모델에 Feedback 루프가 중요하다.
• 검증 : Training error, Validation error

---

3-1. 머신러닝 분류 모델링

분류, 회귀는 출력 변수Y로 구분된다.
underfitting : model complexity가 낮다.
overfitting : model complexity가 높다.

• 분류
  • 제품 불량, 양품 분류
  • 고객이 이탈고객인지, 잔류 고객인지
  • 카드거래가 정상적인지, 사기인지(fraud detection)

---

3-2. KNN

K-Nearest Neighbors, distance-based model, lazy learning algorithm(training data가 활용되지 않고 가만히 있다가, test data와 거리 비교할 때 활용되기 시작해서)
K개의 주변 관측치에 대한 majority voting
간단한 데이터에 대해서는 아직도 많이 활용되고 있다.

• 거리

  • 범주형 변수는 Dummy Variable로 변환하여 거리 계산
  • Euclidean, Manhattan, Minkowski : 거리 구하는 방식

• K의 영향

  • K가 클수록 underfitting, k가 작을수록 overfitting
    

---

3-3 Logistic Regression

선형 회귀(Linear Regression)의 Classification 버전
Y가 범주형인 변수에 대해서 사용하는 회귀 분석을 Logistic Regression이라고 한다.
Logistic Function이라는 변환함수를 사용하기 때문에 Logistic Regression이 되었다. == Logistic Function을 사용하는 Linear Regression 모형

Logistic Regression의 필요성

• 분류 문제의 종속 변수의 속성이 이진 변수일 때 (class가 0, 1)
• 아래 그림을 보면 이진 변수일 때 linear regression은 적합하지 않다. y가 무한히 증가하기 때문이다. 우리는 y 값에 따라 분류되는 예측값이 알고 싶은 것.
  

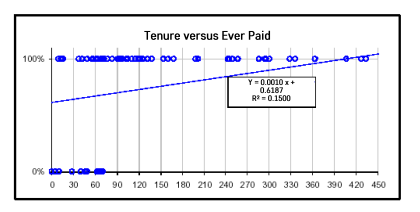
Logistic Regression

Z(u) = e^x / (1+e^x) = 1 / (1+e^-x)

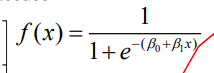
-0을 곱하면 0이 되기 때문에 loss를 minimize하고, 실제 클래스로 분류될 확률을 키워준다.

• cross entropy loss