[yolo v1] 논문 구현

yolo 논문을 토대로 function을 scratch 단계부터 구현하였다.

다음은 논문 링크이다.
You Only Look Once : Unified, Real-Time Object Detection

다음은 구현에 도움을 받은 영상링크이다.
YOLOv1 from scratch

다음은 yolo v1 code 깃허브 링크이다.

시작하기 앞서...

yolo model Architecture

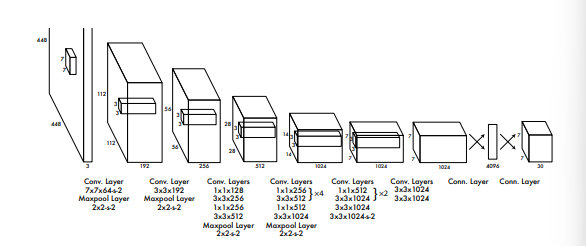
• input 448 x 448 x 3(rgb)
• 7 x 7(kernel) x 64(output filters) x 2(strides)
• 2 x 2(maxpool) x 2(strides)

-> the 448 becomes 224 and then 112 block
(maxPool layer to half the input)

• 3 x 3(kernels) x 192(output filters)

• 2 x 2(maxpool) x 2(strides)

• 1 x 1(kernels) x 128(output filters)

• 3 x 3(kernels) x 256(output filters)

• 1 x 1(kernels) x 256(output filters)

• 3 x 3(kernels) x 512(output filters)

• 2 x 2(maxpool) x 2(strides)

• 1 x 1(kernels) x 256(output filters) x4

• 3 x 3(kernels) x 512(output filters) x4

• 1 x 1(kernels) x 512(output filters)

• 3 x 3(kernels) x 1024(output filters)

• 2 x 2(maxpool) x 2(strides)

• 1 x 1(kernels) x 512(output filters) x2

• 3 x 3(kernels) x 1024(output filters) x2

• 3 x 3(kernels) x 1024(output filters)

• 3 x 3(kernels) x 1024(output filters) x 2

-> 14 becomes 7

• 3 x 3(kernels) x 1024(output filters)
• 3 x 3(kernels) x 1024(output filters)

-> it becomes 7 x 7 x 1024(inputs)
and they reshape. it to become 7 x 7 x 30

finally we gonna have 7 x 7 each for cell and 30 vectors output.
there are 24 cells, one for the probability score of first box with the 4 bounding boxes, second probablitity score of the second box with the 4 bounding boxes.

model.py

import torch 
import torch.nn as nn

architecture_config = [
    (7, 64, 2, 3),
    "M",
    (3, 192, 1, 1),
    "M",
    (1, 128, 1, 0),
    (3, 256, 1, 1),
    (1, 256, 1, 0),
    (3, 512, 1, 1),
    "M",
    [(1, 256, 1, 0), (3, 512, 1, 1), 4],
    (1, 512, 1, 0),
    (3, 1024, 1, 1),
    "M",
    [(1, 512, 1, 0), (3, 1024, 1, 1), 2],
    (3, 1024, 1, 1),
    (3, 1024, 2, 1),
    (3, 1024, 1, 1),
    (3, 1024, 1, 1),
]

• Tuple : (kernel size, ouuput filters, stride, padding)
• `M' : MaxPool
• list : tuples and then last integer represents number of repeats

class CNNBlock(nn.Module):
	def __ini__(self, in_channels, out_channerls, **kwargs):
    	super(CNNBlock, self).__init__() #부모 클래스 초기화
        # this conv layer batch norm(bias = false) and then relu
        self.conv = nn.Conv2d(in_channels, out_channels, bias = false, **kwag)
        self.bachnorm = nn.BachNorm2d(out_channels)
        self.leakrelu = nn.LeakyRelu(0.1)
        
    def forward(self, x):
    	reurn self.leakrelu(self.batchnorm(self.conv(x))

class Yolov1(nn.Moduls):
  def __ini__(self, in_channels=3, **kwargs): # rgb
  	super(Yolov1, self).__init__()
	self.architecture = architecure_config
    self.in_channels = in_channels,
    self.darke = self._create_cov_layers(self.architecure) 
    #buil architeture
    #해당 top 구조를 darknet구조라고 함.
    self.fcs = self._creae_fcs(**kwargs)
  
  def forward(self, x):
  	x = self.darknet(x)
    reurn self.fcs(torch.flatten(x, star_dim = 1)) 
    # return fully connected
    # we don't wan ot flatten the number of examples
    
  def _create_cov_layers(self,  architecure):
  	layers = []
    in_channes = self.in_channels 
    
    for x in architecture :
    	if type(x) == tuple:
        	layers += [
            	CNNBlock(
            	in_channels, out_channels = x[1], kernel_size=x[0], stride = x[2], padding = x[3],
                )
            ]
            
            inchannels = x[1]
            
        elif type(x) == str:
          layer += [nn.MaxPool2d(kernel_size = 2, stride=2)]
        
        elif type(x) == list:
        	conv1 = x[0] # uple
            conv2 = x[1] # tuple
            num_repeats = x[2] # Integer
           	
            for _ in range(num_repeats):
            layer += [
            	CNNBlock(
                	in_channels,
                    conv1[1],
                    kernel_size = conv1[0],
                    stride = conv1[2],
                    padding = conv1[3],
                )
            ]
            
            layer += [
            	CNNBlock(
                	conv1[1], # inchannels is output of the first conv layer
                    conv2[1],
                    kernel_size = conv2[0],
                    stride = conv2[2],
                    padding = conv2[3],
                )
            ]
            
            in_channels = conv2[1]
            
    return nn.Sequential(*layer)
    # start layer is gonna unpack
    # ann nn convert to sequenial
    
	def _creaet_fcs(self, split_size, num_boxes, num_classes):
    	
    	S, B, C = split_size, num_boxes, num_classes
        return nn.Sequential(
        	nn.Flatten(), # because we're gonna send it to a linear layer
            nn.Linear(1024 * S * S, 4096)
            # thoes many nodes so use 496 instead 4096
            # Orginal paper this sholud be 4096
            nn.Dropout(0.5)
            nn.LeakyReLU(0.1)
           	nn.Linear(496, S * S * (C + B * 5),
            # (S, S, 30) where C+B*5 = 30
        )
            

TEST CODE

def test(S = 7, B = 2, C = 20) :
	model = Yolov1(split_size = S, num_boxes = B, num_classes = C)
    x = torch.randn((2, 3, 448, 448))
    print(model(x).shape)

loss.py

loss function

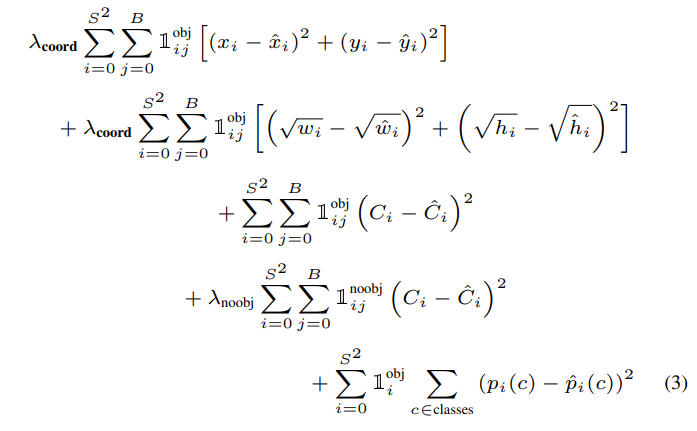
the boxes

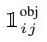
• identitiy funcion and we're only gonna do that if there's an object in the cell and also if the bounding box j responsible for outputting that bounding box.
• one or zero
• if there's a box in cell i ad i is gonna go from zero to S squared. so it goes thorough every cell in our image
• if there's an object in cell i but we need a requiremen tha bounding box j was responsible for outputting that bounding box.
• and the one that has highest iou, and then send to right that.

• the only difference here is that we have the square root.
• we have a very large bounding box and we take those subract and it squared for very large Bbox. (if we would have a large Bbox.)
• smaller Bboxes equally much as we do for large Bboxes.

C, probability tha there's a box in the cell

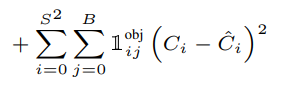
• we 're only going to take the one that highes IOU.
• there're sort of responsible for predicting. and so we go through for each cell and every Bbox.

there was no object in the cell.

what object is it in this Box?

• only use a regression based loss for everything.

import torch 
import torch.nn as nn
form utils import intersection_over_union

class YoloLoss(nn.Module):
	def __init__(self, S = 7, b = 2, c = 20):
    	super(YoloLoss, self).__init__()
        self.mse = nn.MSELoss(reduction = "sum")
        self.S = S
        self.B = B
        self.C = C
        self.lambda_noobj = 0.5
        self.lamda_coord = 5
        
     def forward(self, predictions, target):
		predictions = predictions.reshapes(-1, self.S, self.B, self.C + self.B * 5)
        # 예시의 수, 없으면 -1

		# IOU 계산
        # 0~ 19 are class probabilites.
        # 20 is class score
        # 21 to 25 4 Bbox's values
        # AND there's only one target so we're still going o have target 21 to 25
        
        intersection_over_union(predictions[..., 21:25], target[..., 21:25]
        intersection_over_union(predictions[..., 26:30], target[..., 21:25]
        # we are using torch.cat
        torch.cat([iou_b1.unsqueeze(0), iou_b2.unsqueeze(0)], dim = 0)
        # we concatenate them along the dimension zero that we just unsqueezed.
        iou maxes, bestbox = torch.max(ious, dim = 0)
        # which and how much
        # which one was reposible for that cell.
        exists_box = target[..., 20].unsqueeze(3) # zero ore one. if there's an object in the cell. 
        # we take the 20th index that last dimension disapears. so what we're doing on squeeze.
        # identity_object_i
        
        #  for Box coordinates
        box_predictions = exists_box * (
        	(
            	best_box * predicions[..., 26:30] # 만약 두번째 박스가 선택되었다면.
                + (1 - best_box) * predictions[..., 21:25] # 만약 첫번째 박스가 선택되었다면.
            )
        )
        
        box_targets = torch.sqrt(target[..., 21:25])
        
        # box_prediction이 0이라면 -무한대 이기 떄문에 + 1e-6
        # nagative를 막기 위해 abs
        # to make sure that the sign of the gradient 
        box_predictions[..., 2:4] = torch.sign(box_predictions[..., 2:4]) * torch.sqrt(torch.abs(box_predictions[..., 2:4] + 1e+6)
        
        # targets는 nagative가 없음.
        # sxs -> ...
        box_targes[..., 2:4] = torch.sqrt(box_targets[..., 2:4]
        
        #mse
        # torch.flatten of box predictions
        # why dim is -2 is because we want to flatten everything in front
        # all of these are sort of separate examples in a way 
        # we send to n times s times s by 4 Bbox -> a MSE expects the input shape to 
        # n dim is going to be -2
        
        # (N, S, S, 4) -> (N*S*S, 4)
        box_loss = self.mse(
        	torch.flatten(box_predictions, end_dim =2),
            torch.flatten(box_targets, end_dim = -2)
        )
        
        # object loss
        # which on is responsible?
        pred_box = (
        bestbox * predictions[..., 25:26] + (1 - bexbox) * predictitons[..., 20:21]
        
        # (N*S*S, 1)
        # all of these cells for each examples
        # n times s times
        # we don't have to specifiy the start dimension
        # there are checking exists box for the identity.
        object_loss = self.mse(
        	torch.flatten(exists_box * pred_box),
            torch.flatten(exists_box * target[..., 20:21]
        )
        
        # no object
        # (N, S, S, 1) -> (N, S*S)
        no_object_loss = self.mse(
            torch.flatten((1 - exists_box) * predictions[..., 20:21], start_dim=1),
            torch.flatten((1 - exists_box) * target[..., 20:21], start_dim=1),
        )
        
        no_object_loss += self.mse(
            torch.flatten((1 - exists_box) * predictions[..., 25:26], start_dim=1),
            torch.flatten((1 - exists_box) * target[..., 20:21], start_dim=1)
        )
        
        # for class loss
        # (N, S, S, 20) -> (N * S * S, 20)
        
        class_loss = self.mse(
            torch.flatten(exists_box * predictions[..., :20], end_dim=-2,),
            torch.flatten(exists_box * target[..., :20], end_dim=-2,),
        )
        
        loss = (
            self.lambda_coord * box_loss  # first two rows OF LOSS in paper
            + object_loss  # third row in paper
            + self.lambda_noobj * no_object_loss  # forth row
            + class_loss  # fifth row
        )

        return loss

these are not relative to cell but entire image.

the first thing is the class probabliy
the second thing is mid point of the height
the third thing is mid point of the width

DATASET

# csv file, image directory 
# 데이터 증감 하지 않음.

# len
# data set loading

# label_path 연결 
# txt 파일 엶

# we replace new line with just empty space.
# it is a string when we are doing flat we're converting it to a string.

# box에 라벨과 x,y 좌표 및 가로 세로 길이 추가.

# box를 tensor로 변경.

# 이미지 증감 하지 않음.

# 전체이미지가 아니라 한 셀의 한 바운딩박스에 대해 계산