관계 대수
관계 대수 개요
Statement(문장) : a = 1, b = 2와 같이 값이 바뀌는 경우로 명령문이라고도 한다.
Expression(식) : a + b과 같은 경우로 표현식이라고도 한다.
c = a + b는? a + b는 Expression, c = 까지 포함하면 Statement이다.
DB에서 c = a + b라는 식이 있다.
이때, a도 릴레이션, b도 릴레이션이다. 관계형 데이터베이스에선 모든 변수가 릴레이션이다. 타입이 릴레이션 하나!
필수 관계 연산자
| 연산자 | 표기법 | 단항 또는 이항 |
|---|---|---|
| 셀렉션(selection) | δ | 단항 |
| 프로젝션(projection) | π | 단항 |
| 합집합(union) | ∪ | 단항 |
| 차집합(difference) | - | 단항 |
| 카티션 프로덕트(cartesian product) | × | 단항 |
유도된 관계 연산자
| 연산자 | 표기법 | 단항 또는 이항 |
|---|---|---|
| 동등 조인(equijoin) | ⋈ | 이항 |
| 세타 조인(theta join) | ⋈θ | 이항 |
| 자연 조인 | ⋈N | 이항 |
| 세미 조인 | ⋉ and ⋊ | 이항 |
| 외부 조인 Left | ⟕ | 이항 |
| 외부 조인 Right | ⟖ | 이항 |
| 외부 조인 Full | ⟗ | 이항 |
셀렉션과 프로젝션
- 릴레이션에서 투플들을 선택(Selction)할 수 있는 연산자 시그마( δ )
- 필드들을 추출(Projection)할 수 있는 연산자 파이 ( π )
- 단일 릴레이션에 있는 데이터를 조작하는데 사용
- 셀렉션 연산자 δ는 셀렉션 조건을 통해 얻을 투플들을 명세
- 비교 연산자 <, ⇐, =, ≠, >= > 중의 하나를 op라고 할 때 애트리뷰트 op 상수 또는 애트리뷰트 op 애트리트뷰트 형태의 항을 불리언으로 조합
- 프로젝션 연산자 π는 릴레이션의 필드들을 추출
집합 연산
- 합집합, 교집합, 차집합, 카티션 프로덕트와 같은 표준 집합 연산
합집합(Union, ∪)
인스턴스 R이나 인스턴스 S 모두에 속하는 투플들을 포함하는 릴레이션 인스턴스를 만듦
R과 S는 합병 가능해야 하며, 결과 스키마는 R의 스키마와 동일
교집합(Intersection, ∩)
R ∩ S는 양쪽에 함께 속하는 모든 투플로 구성된 릴레이션 인스턴스를 만듦
차집합(Set-different, – )
R – S는 R에는 속하고 S에는 속하지 않는 투플로 구성된 릴레이션 인스턴스를 만듦
지원하지 않는 데이터베이스도 많다. MySQL도 지원하지 않는다.카디션 프로덕트(Cartisian Product, X)
R X S는 R의 모든 필드와 S의 모든 필드를 순서대로 가지는 스키마의 릴레이션 인스턴스를 만듦
R X S는 r∈R, s∈S 쌍에 대하여 투플 <r, s>를 하나씩 가짐
이름 바꾸기
- 릴레이션에서 필드의 이름을 변경(Renaming)할 수 있는 연산자 로우( ρ )
- 관계 대수식 안에서 이름 충돌이 발생할 수 있음
- 관계 대수식 안에서 릴레이션 인스턴스의 이름을 주는 것이 편리함
- 긴 대수식을 작은 부분으로 나누어 결과 인스턴스에 이름을 줄 수 있도록 하는 것이 편리함
조인
| 종류 | 기호 | 기능 |
|---|---|---|
| 동등 조인 | ⋈ | 두 릴레이션간의 값을 가진 집합 |
| 세타 조인 | ⋈θ | 두 릴레이션 간의 비교 조건에 만족하는 집합 |
| 자연 조인 | ⋈N | 동등 조인에서 중복 속성을 제거 |
| 세미 조인 | ⋉ and ⋊ | 자연 조인 후 기호의 열린쪽의 속성을 제거 |
| 외부 조인 Left | ⟕ | 자연 조인 후 왼쪽의 모든 값을 추출, 값이 없을 경우 한쪽의 값을 NULL로 채용 |
| 외부 조인 Right | ⟖ | 자연 조인 후 오른쪽의 모든 값을 추출, 값이 없을 경우 한 쪽의 값을 NULL로 채용 |
| 외부 조인 Full | ⟗ | 자연 조인 후 양쪽의 모든 값을 추출, 값이 없을 경우 한 쪽의 값을 NULL로 채용 |
자연조인(⋈N, NATURAL JOIN)
자연조인은 조인 조건이 없는 조인으로 테이블의 같은 이름의 속성이 있는 경우에, 같은 이름의 속성으로 조인을 실행한다. 동등 조인에서 중복 속성을 제거
MySQL 코드
SELECT p.productName, c.CategoryName
FROM
Product AS p NATURAL JOIN Category c;
# 위와 같다.
SELECT p.productName, c.CategoryName
FROM
(SELECT * FROM Product) AS p NATURAL JOIN (SELECT * FROM Category) AS c;결과
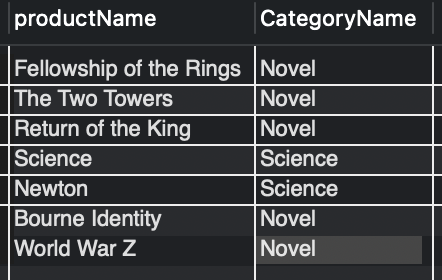
동등 조인 (⋈, NATURAL JOIN)
MySQL에선 NATURAL JOIN과 같다. 하지만 데이터베이스마다 NATURAL JOIN 명령어가 없는 경우가 있다.(ex - MSSQL) 그럴땐 inner join으로 같은 조인을 구현할 수 있다.
MySQL 코드
SELECT * FROM Product NATURAL JOIN Category;INNER JOIN을 사용한 코드 <- 모든 DBMS에서 사용 가능
SELECT * FROM Product INNER JOIN Category ON Product.CategoryNo = Category.CategoryNo;관계 해석
관계 해석은 관계 대수의 대안입니다. 관계 대수가 절차형인데 반하여 관계 해석은 비절차형, 즉 명세형으로서 계산 방법을 명세함이 없이 답의 집합을 표현할 수 있습니다.
DB 필요한 능력
- 엔지니어링 능력 : DB 설계하고 안죽이는 능력
- 프로그래밍 능력 : SQL 쿼리
