시간 복잡도란?

시간 복잡도(Time Complexity)는 알고리즘이 문제를 해결하는데 필요한 시간이 얼마나 걸리는지를 나타내는 척도이다. 이는 일반적으로 알고리즘 입력의 크기에 대해 실행 시간이 어떻게 증가하는지를 나타내는 함수로 표현된다. 시간 복잡도 분석은 최악의 경우, 최선의 경우, 평균적인 경우 등의 시나리오를 고려한다.

• 빅 오 표기법 (O-Notation)
• 오메가 표기법 (Ω-Notation)
• 세타 표기법 (Θ-Notation)

---

1. O-Notation (최악의 경우)

가장 널리 사용되는 표기법으로, 알고리즘의 최악의 경우(worst case) 성능을 나타낸다. 알고리즘의 상한을 나타낸다.

두 함수 $f(n), g(n)$이 있을 때,
모든 $n \ge n_0$에 대하여 $0 \le f(n) \le cg(n)$을 만족하는 $c \gt 0$, $n_0 \gt 0$인 상수가 존재하면,
$f(n) = O(g(n))$이다.

Example

$5n^3 + 2n + 8 = O(n^3)$
$c$를 15로, $n_0$를 1로 설정할 경우, 위의 조건을 만족한다.

---

2. Ω-Notation (최선의 경우)

알고리즘의 최선의 경우(best case) 성능을 나타내는 표기법이다. 알고리즘의 하한을 나타낸다.

두 함수 $f(n), g(n)$이 있을 때,
모든 $n \ge n_0$에 대하여 $0 \le cg(n) \le f(n)$을 만족하는 $c \gt 0$, $n_0 \gt 0$인 상수가 존재하면,
$f(n) = Ω(g(n))$이다.

Example

$5n^3 + 2n + 8 = Ω(n^3)$
$c$를 1로, $n_0$를 1로 설정할 경우, 위의 조건을 만족한다.

---

3. Θ-Notation (평균적인 경우)

알고리즘의 평균적인 경우(average case) 또는 일반적인 경우를 나타내는 표기법으로, 알고리즘의 상한과 하한이 동일할 때 사용된다.

두 함수 $f(n), g(n)$이 있을 때,
모든 $n \ge n_0$에 대하여 $0 \le c_1g(n) \le f(n) \le c_2g(n)$을 만족하는 양수인 상수 $c_1, c_2, n_0$가 존재하면,
$f(n) = Θ(g(n))$이다.

Example

$5n^3 + 2n + 8 = Θ(n^3)$

같은 수식에 대해, $O(n^3)$과 $Ω(n^3)$이 성립하므로 $Θ(n^3)$ 또한 성립한다.
$Θ(g(n)) = O(g(n)) \ \cap \ Ω(g(n))$ 이라고 할 수 있다.
아래와 같이 $5n^3 + 2n + 8 = Θ(n^3)$를 증명할 수도 있다.

$5n^3 + 2n + 8 \le 5n^3 + 2n^3 + 8n^3 = 15n^3 \ (for \ all \ n \ge 1)$
$5n^3 \le 5n^3 + 2n + 8 \ (for \ all \ n \ge 1)$

$g(n) = n^3$
$f(n) = 5n^3 + 2n + 8$

$There \ exist \ constants \ c_1 = 5, c_2 = 15, n_0 = 1$
$0 \le c_1g(n) \le f(n) \le c_2g(n) \ (for \ all \ n \ge 1)$

$5n^3 + 2n + 8 = Θ(n^3)$

---

1. Big-O 시간 복잡도 표

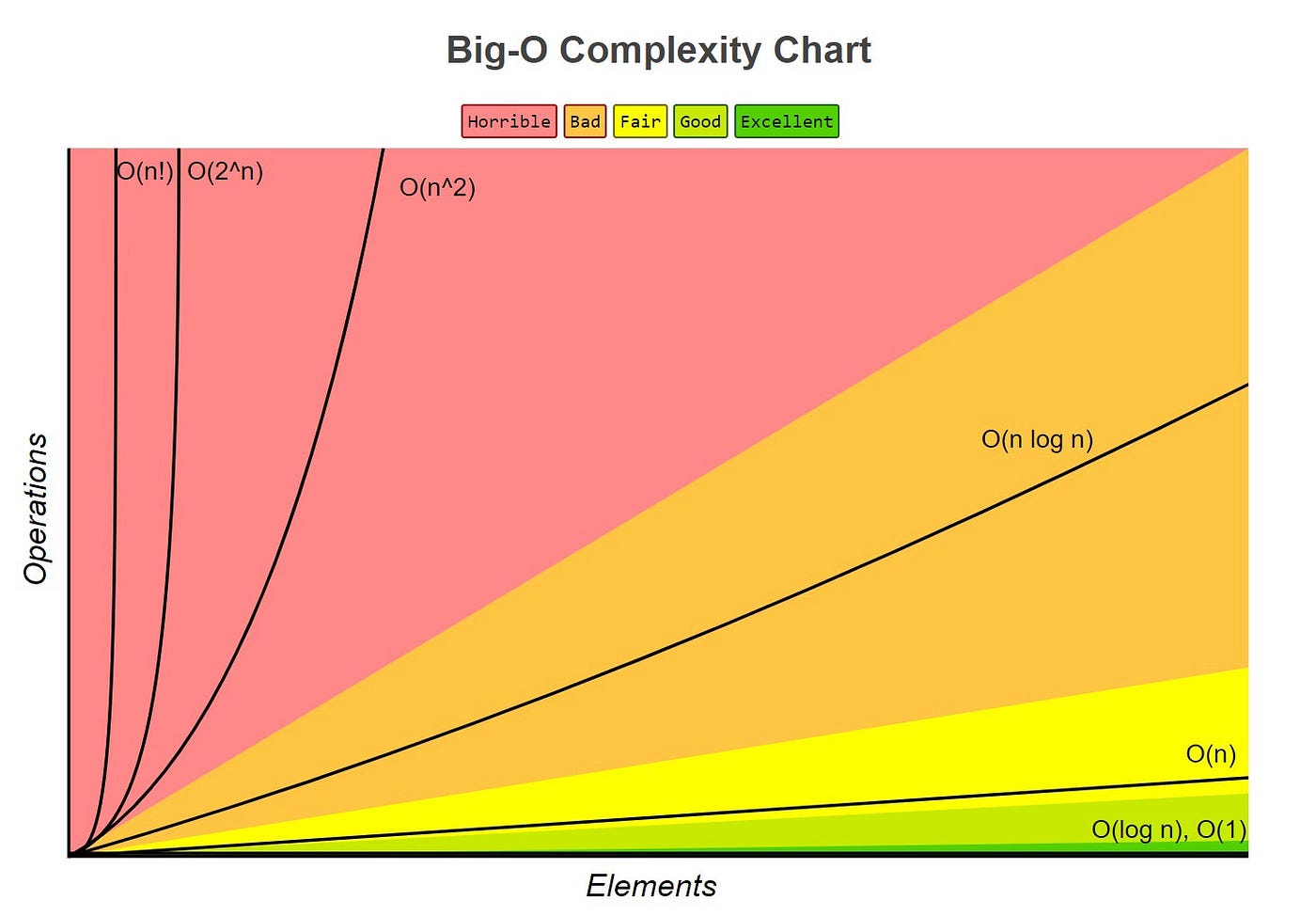
• $O(1)$ (상수 시간)
  입력 데이터의 크기와 상관없이 항상 일정한 시간이 소요되는 알고리즘이다. 예를 들어, 배열의 특정 인덱스에 접근하는 작업이 이에 해당한다.

• $O(\log n)$ (로그 시간)
  알고리즘의 실행 시간이 입력 데이터의 로그에 비례하여 증가하는 경우이다. 이런 복잡도를 갖는 대표적인 예로 이진 검색이 있다.

• $O(n)$ (선형 시간)
  알고리즘의 실행 시간이 입력 데이터의 크기에 비례하여 선형적으로 증가한다. 예를 들어, 배열의 모든 요소를 한 번씩 검사하는 알고리즘이 이에 해당한다.

• $O(n \log n)$
  이 복잡도를 갖는 알고리즘은 데이터의 크기에 비례하여 증가하는 동시에 그 증가율에 로그를 곱한 만큼 증가한다. 대표적인 예시로 퀵소트나 병합 정렬이 있다.

• $O(n^2)$ (이차 시간)
  알고리즘의 실행 시간이 입력 데이터의 크기의 제곱에 비례하여 증가한다. 예를 들어, 두 배열의 모든 쌍을 비교하는 버블 정렬이 여기에 속한다.

• $O(2^n)$ (지수 시간)
  이 복잡도를 갖는 알고리즘은 데이터 크기가 증가함에 따라 실행 시간이 지수적으로 증가한다. 재귀적으로 모든 경우의 수를 탐색하는 알고리즘들이 이에 해당한다. 예시로 피보나치 수열을 재귀적으로 계산하는 방법이 있다.

• $O(n!)$ (팩토리얼 시간)
  입력 데이터의 크기에 대해 팩토리얼로 시간 복잡도가 증가하는 경우이다. 예를 들어, 모든 가능한 순열을 생성하거나 검사할 때 이 복잡도가 나타난다. 대표적으로 브루트 포스로 풀리는 외판원 문제(TSP)가 있다.