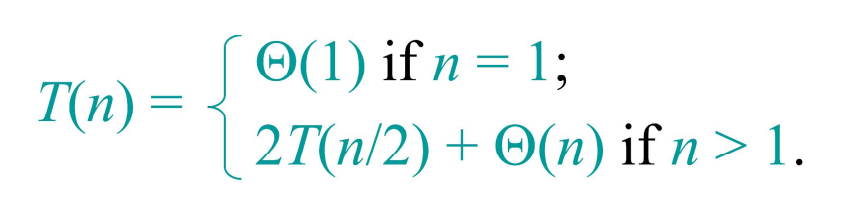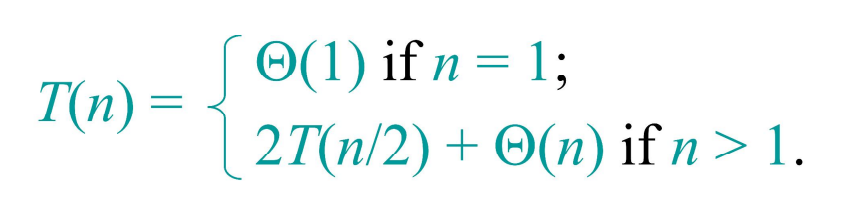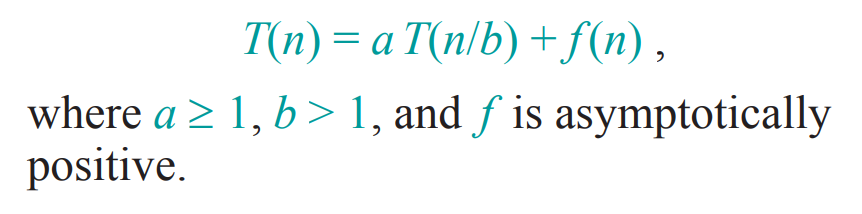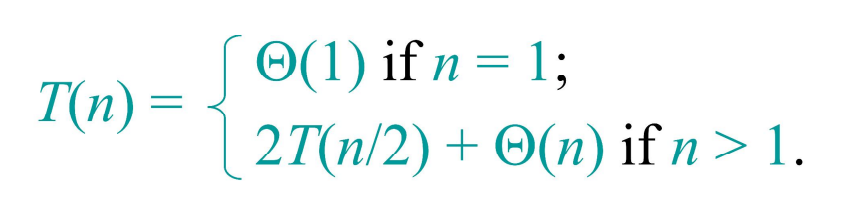
위는 합병 정렬(Merge sort)의 시간 복잡도를 나타낸다. 위와 같은 재귀식 형태로는 알고리즘의 시간 복잡도를 정확히 알 수 없다. 점화식 풀이를 위해, 아래의 3가지 방법을 사용할 수 있다.

• 치환법 (Substitution method)
• 재귀 트리 (Recursion-tree)
• 마스터 정리 (Master method)

---

1. 치환법 (Substitution method)

치환법은 재귀적인 알고리즘의 시간 복잡도를 추측하고, 그 추측값이 실제로 성립하는지 증명하는 방법이다. 이를 위해 증명은 아래의 세 단계로 나누어진다.

1) 가설 설정 (Guess the form of the solution)

$T(n) = 2T(n/2) + n$ 재귀식의 시간 복잡도를 구하는 예시이다. 먼저 복잡도의 형태를 추측해야 하는데, 예를 들어, $T(n) = O(n\ log\ n)$이라고 가정해 볼 수 있다.

2) 귀납법을 통한 검증 (Verify by induction)

가정을 증명하기 위해 귀납법을 사용한다. 이를 위해 $n$보다 작은 모든 양수와, 임의의 상수 $c$에 대해 $T(n) \le cn\ log\ n$이 성립한다고 가정한다. 이 가정을 바탕으로 $T(n) \le cn\ log\ n$를 증명해야 한다.

$T(n) = 2T(n/2) + n\\ \le 2(c(n/2)\ log\ (n/2)) + n\\ = cn\ log\ (n/2) + n\\ = cn\ log\ n − cn\ log\ 2 + n\\ = cn\ log\ n − cn + n\\ = cn\ log\ n − (cn - n) \ \textcolor{red}{\leftarrow} \textcolor{red}{desired-residual}\\ \le cn\ log\ n \ \textcolor{red}{\leftarrow} \textcolor{red}{desired}$

$T(n) \le cn\ log\ n$를 가정했기 때문에, $2T(n/2)$는 항상 $2(c(n/2)\ log\ (n/2))$ 보다 작게 되고, 위와 같이 증명이 성립한다. 위의 증명과 같이 $desired-residual$ 형식을 만드는 것을 목표로 해야 하며, 해당 증명의 경우 $c \ge 1$인 경우 성립한다고 할 수 있다.

3) Base Case

위의 증명에 따라 $T(n) \le cn\ log\ n$이 성립한다면, $T(1) \le 0$ 또한 성립해야 하는데, 이는 사실이 아니다. 이와 같이 귀납적 증명의 기저(Base Case)가 성립하지 않는 경우, 귀납적 증명의 범위를 변경하여 쉽게 해결할 수 있다. 예시의 경우, $n \gt 1$로 기저를 설정하면 증명이 성립하게 된다.

위의 과정에 따라 증명에 성공하게 되더라도, Tighter Upper Bound를 찾기 위해 증명을 반복해야 할 수 있다. 예시에서는 원활한 설명을 위해 처음부터 $O(n\ log\ n)$을 가정하였지만, 만약 $O(n^2)$을 가정하였을 경우, 증명에 성공하더라도 최선의 경우인 $O(n\ log\ n)$를 증명할 때까지 위의 과정을 반복해야 한다.

---

2. 재귀 트리 (Recursion-tree)

재귀 트리 (Recursion-tree)는 재귀 함수의 각 호출과 그 결과로 발생하는 추가 호출을 트리 구조로 시각화한 것이다. 예시인 $T(n) = 2T(n/2) + n$의 경우, 아래의 그림과 같이 표현될 수 있다.

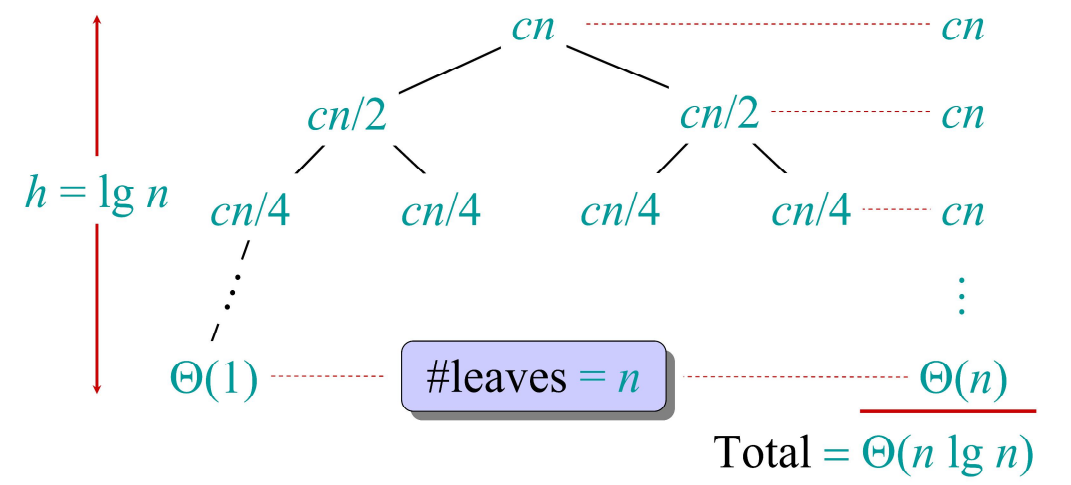
위의 재귀 트리의 높이는 $log\ n$, 각 레벨의 비용은 모두 $cn$으로 표현될 수 있고, 전체 비용을 합산한 결과 $O(n\ log\ n)$이라는 것을 알 수 있다. 재귀 트리는 시각화를 통해 재귀 함수의 각 단계에서 발생하는 비용을 쉽게 이해할 수 있도록 돕지만, 노드를 '...'와 같은 형태로 표현하는 방법론이기에 부정확할 수 있다는 단점이 존재한다.

---

3. 마스터 정리 (Master method)

마스터 정리는 특정한 형태의 재귀식을 간단하게 계산하는 방법이다. 마스터 정리를 사용할 수 있는 재귀식의 형태는 아래와 같다.

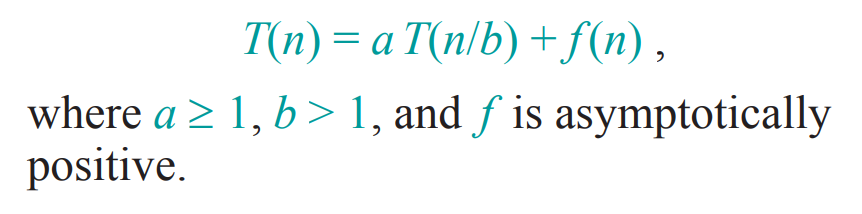
본 설명에서는 마스터 정리의 증명을 다루지 않고, 각 Case에 따른 마스터 정리의 사용을 중심으로 설명을 진행한다. 먼저, $f(n)$을 $n^{log_ba}$와 비교한다.

1) Case 1

$f(n) = O(n^{log_ba-\epsilon})$

이 경우, $f(n)$이 $n^{log_ba}$보다 느리게 증가한다고 할 수 있다.
마스터 정리에 의해, $T(n) = O(n^{log_ba})$

Example: $T(n) = 4T(n/2) + n$
$a = 4,\ b = 2\ {\rightarrow}\ n^{log_ba} = n^2,\ f(n) = n$
Case 1.
$f(n) = n = O(n^{log_ba-\epsilon}) = O(n^{2 – \epsilon})\ for\ \epsilon = 1$
$\therefore\ T(n) = O(n^2)$

2) Case 2

$f(n) = \Theta(n^{log_ba}$)

이 경우, $f(n)$와 $n^{log_ba}$이 비슷한 속도로 증가한다고 할 수 있다.
마스터 정리에 의해, $T(n) = O(n^{log_ba}\ log\ n)$

Example: $T(n) = 4T(n/2) + n^2$
$a = 4,\ b = 2\ {\rightarrow}\ n^{log_ba} = n^2,\ f(n) = n^2$
Case 2.
$f(n) = n^2 = \Theta(n^{log_ba})$
$\therefore\ T(n) = O(n^2\ log\ n)$

3) Case 3

$f(n) = \Omega(n^{log_ba+\epsilon}$)

이 경우, $f(n)$이 $n^{log_ba}$보다 빠르게 증가한다고 할 수 있다.
임의의 상수 $c<1$에 대하여, $af(n/b) \le cf(n)$를 만족하는 Regularity Condition을 충족하는 경우, 마스터 정리를 사용할 수 있다.
마스터 정리에 의해, $T(n) = O(f(n))$

Example: $T(n) = 4T(n/2) + n^3$
$a = 4,\ b = 2\ {\rightarrow}\ n^{log_ba} = n^2,\ f(n) = n^3$
Case 3.
$f(n) = n^3 = \Omega(n^{log_ba+\epsilon}) = \Omega(n^{2 + \epsilon})\ for\ \epsilon = 1$
$and,\ 4(n/2)^3 \le cn^3\ for\ c = 1/2\ (Regularity\ Condition)$
$\therefore\ T(n) = O(n^3)$