DL4CV lecture 6: Backpropagation

How to compute gradients?

1. Derive on paper(Bad Idea): 실제 식을 미분하는것
   • 복잡한 모델에서 불가능
   • 손실함수를 바꾸면 또 다시 미분해야됨
2. Computational Graph(Better Idea)

Computational Graph

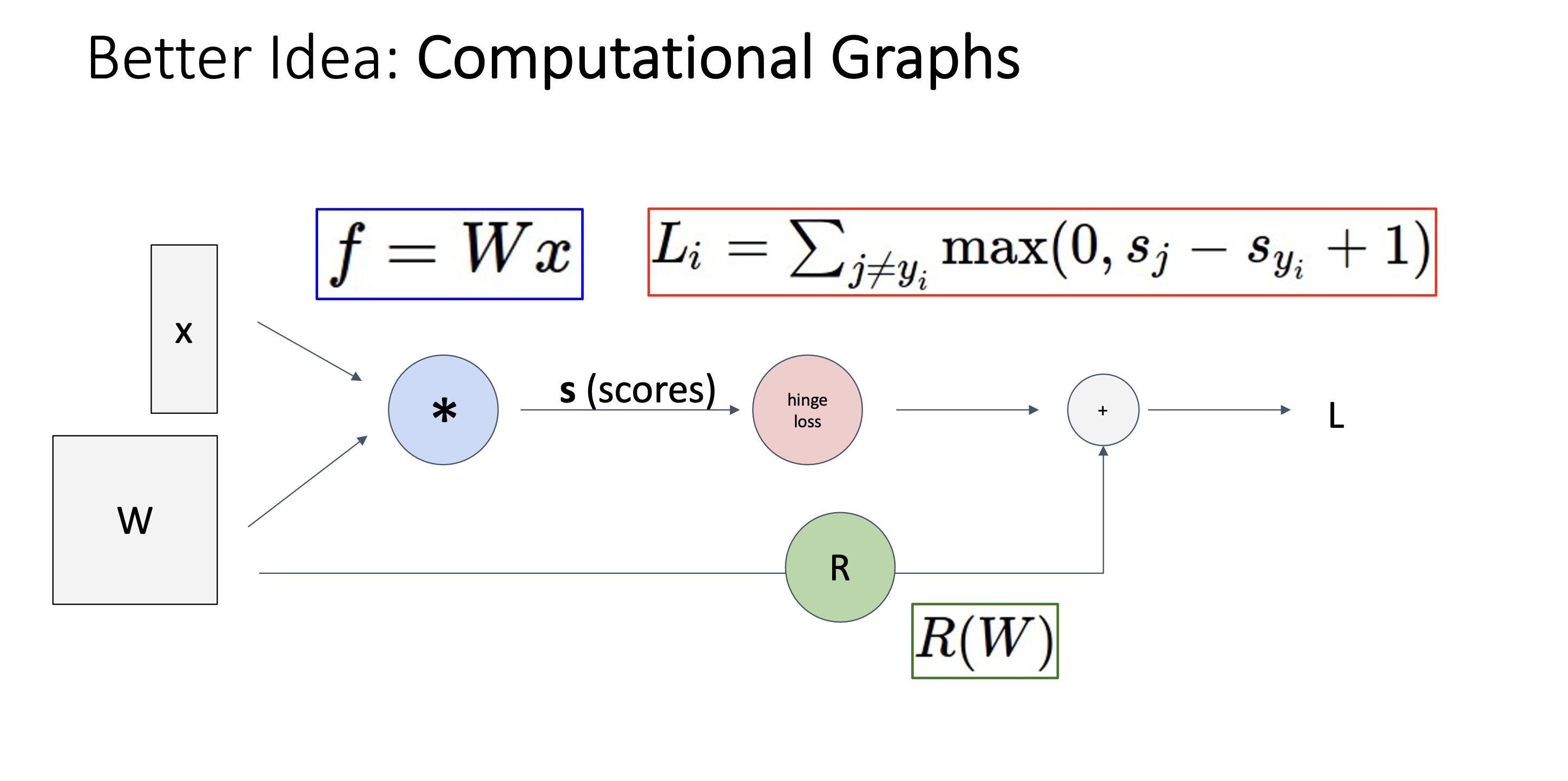
• 수식을 다음과 같이 graph로 표현

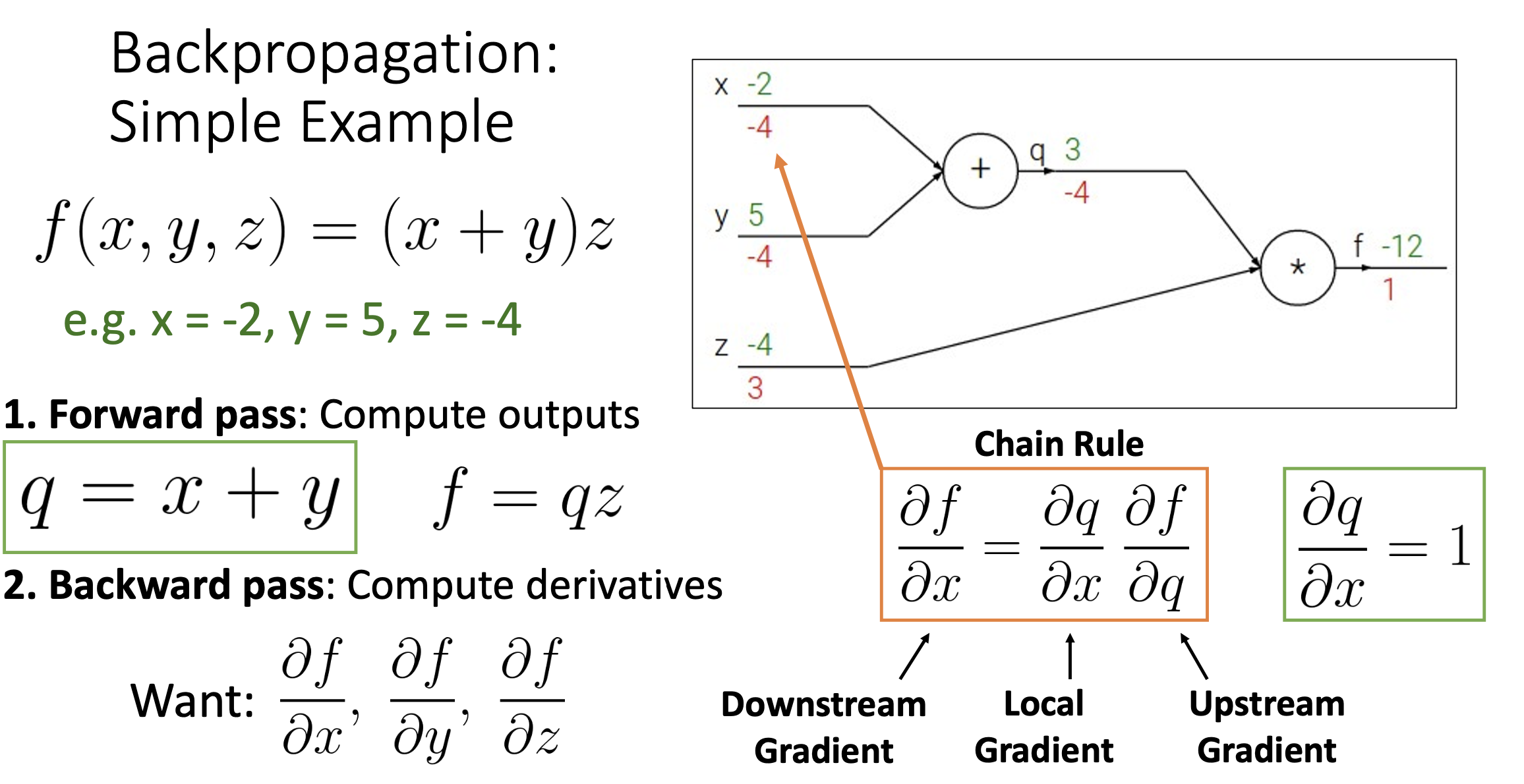
역전파 과정
1. Forward Pass: 왼쪽에서 오른쪽으로 output계산
2. Backward Pass: 오른쪽에서 왼쪽으로 base case 1부터 진행하여 Local Gradient를 계산해가며 각 변수들이 Loss에 얼마나 변화를 끼치는지 계산

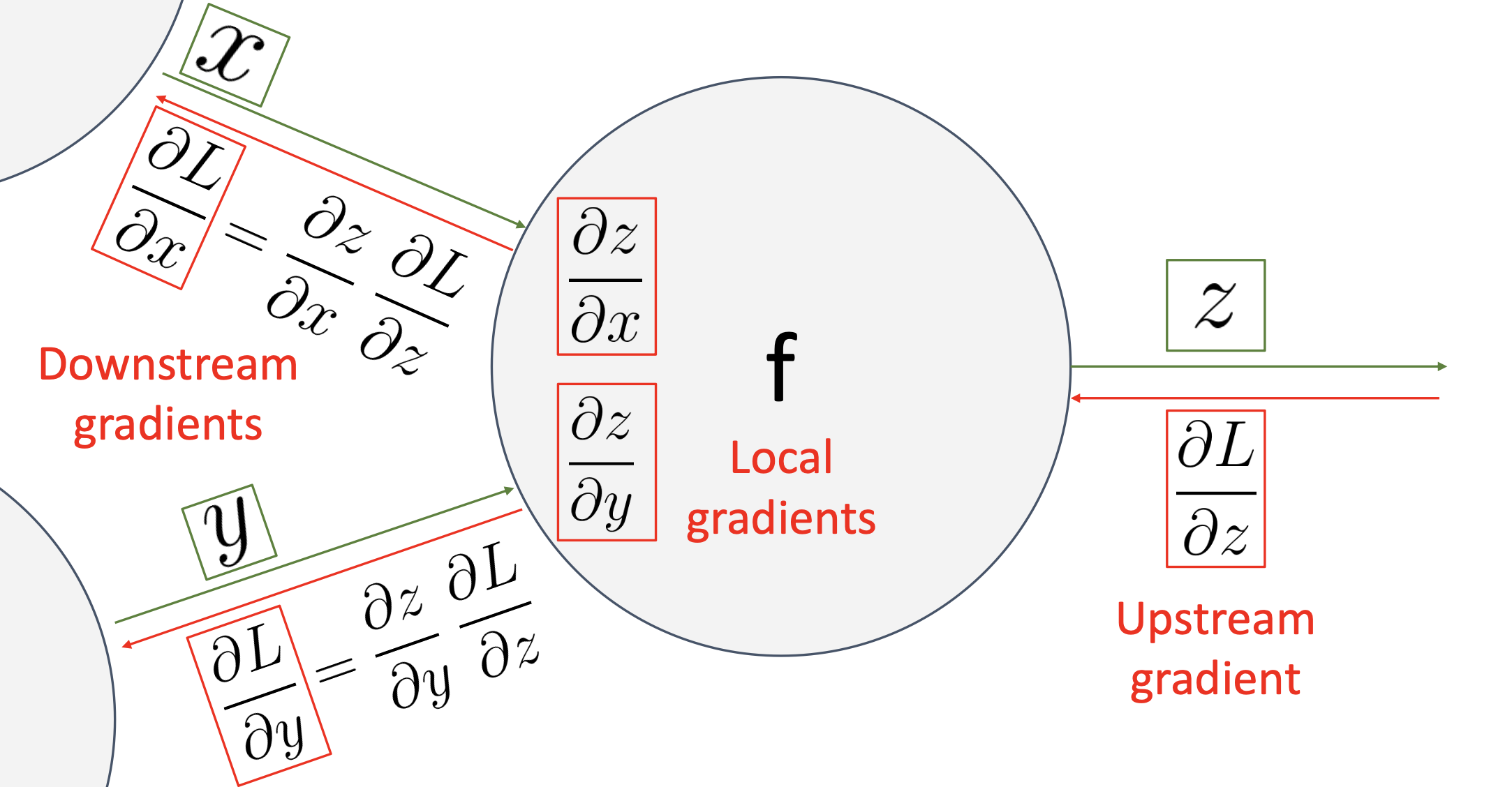
• 한 노드를 극소적으로 봤을때,
• Loss쪽에서 오는 미분값(Loss 변화량 포함)을 Upstream Gradient라고 한다.
• 노드에서 계산되는 미분값(Loss 변화량이 포함되어있지 않음)을 Local Gradients라고 한다.
• Upstream Gradient와 Local Gradients를 Chain Rule을 통해 곱하면 이전노드 변수에 따른 Loss의 변화량은 Down Gradients가 나오게 된다.
• 노드에서는 단순히 이전과 이후 노드에 대한 Local Gradients를 구해가다 보면, 결국에는 구하고자하는 마지막 노드에서의 미분값을 구하게된다.

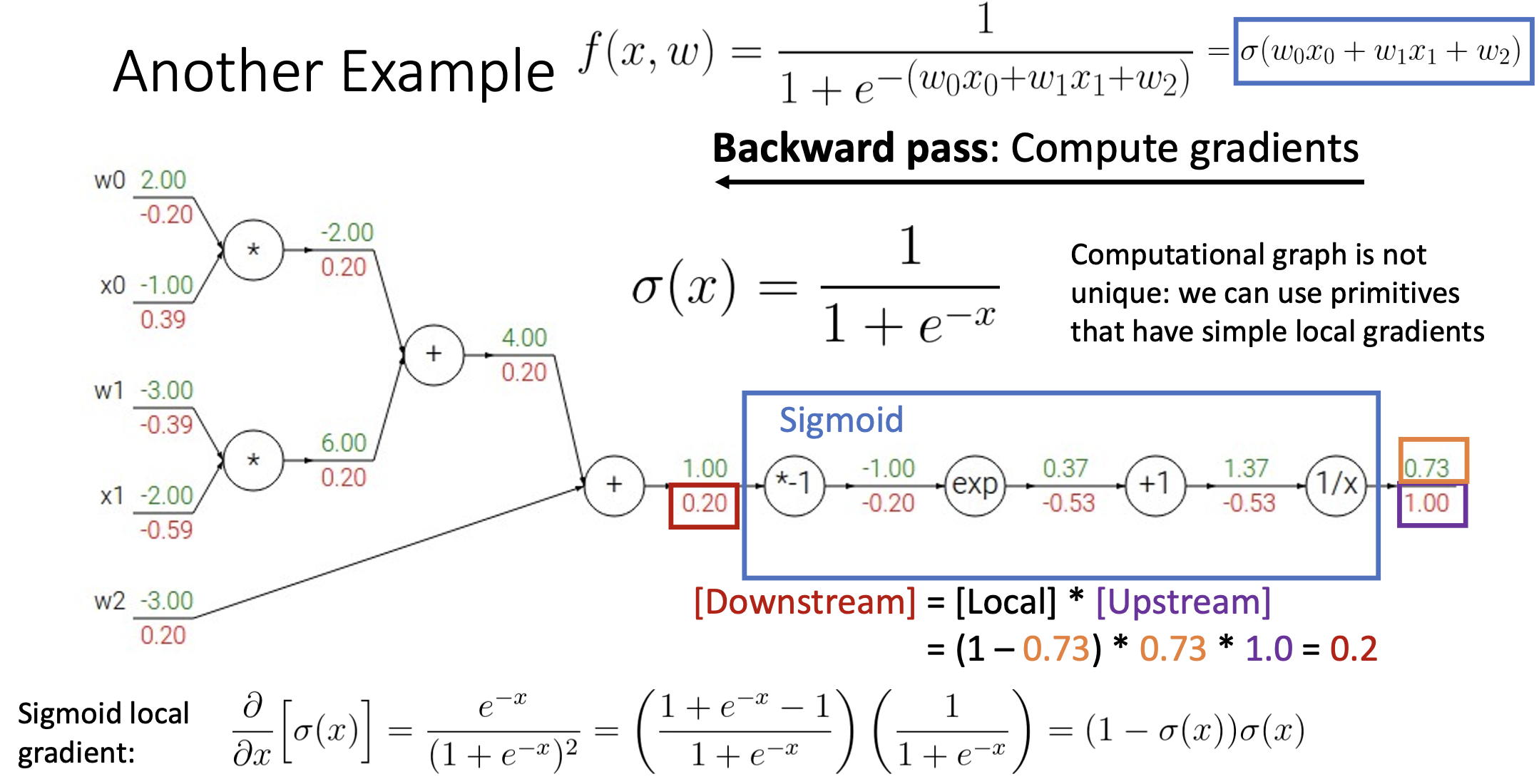
• sigmoid함수와 같이 미분식을 합쳐서 구할 수 있는 것은 Backward Pass 할 때 편하게 역전파 값을 구함

Patterns in Computational Graph

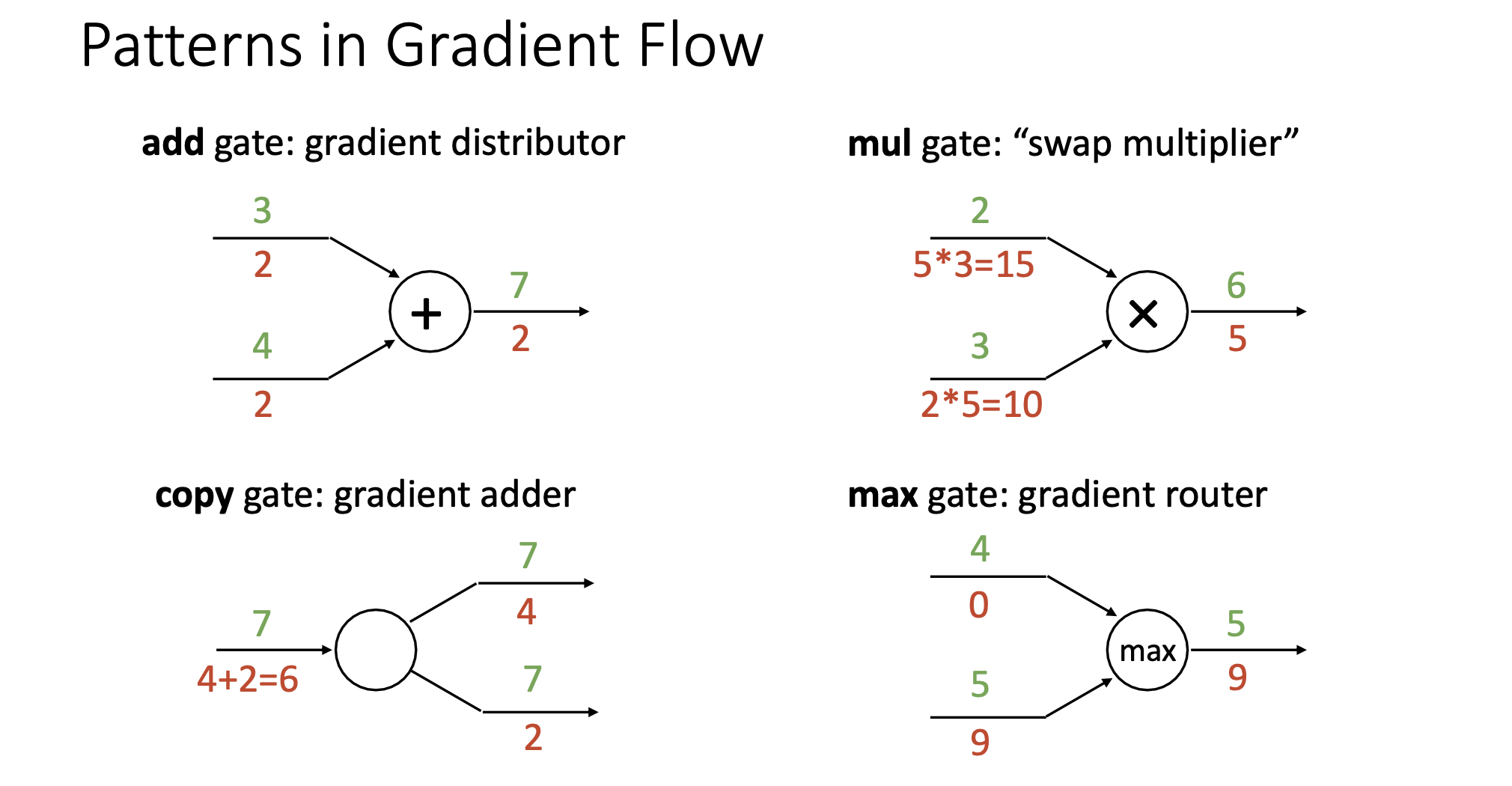
• add gate: f(x,y) = x + y, 역전파 값이 copy됨
• copy gate: 역전파 값을 더하면 됨
• mul gate: f(x,y) = x * y, 역전파 값에 순전파로 온 값을 바꿔 곱하면 됨
• max gate: f(x,y) = max(x,y), max 값에 기여한 노드에 역전파 값을 전파하고, 나머지 노드에는 0으로 들어감

Backprop with Vectors

• 위에서 설명했던 Computational Graph는 scalar값에 대해서 설명했지만, 실제 데이터는 고차원의 N-dimentional Vector임

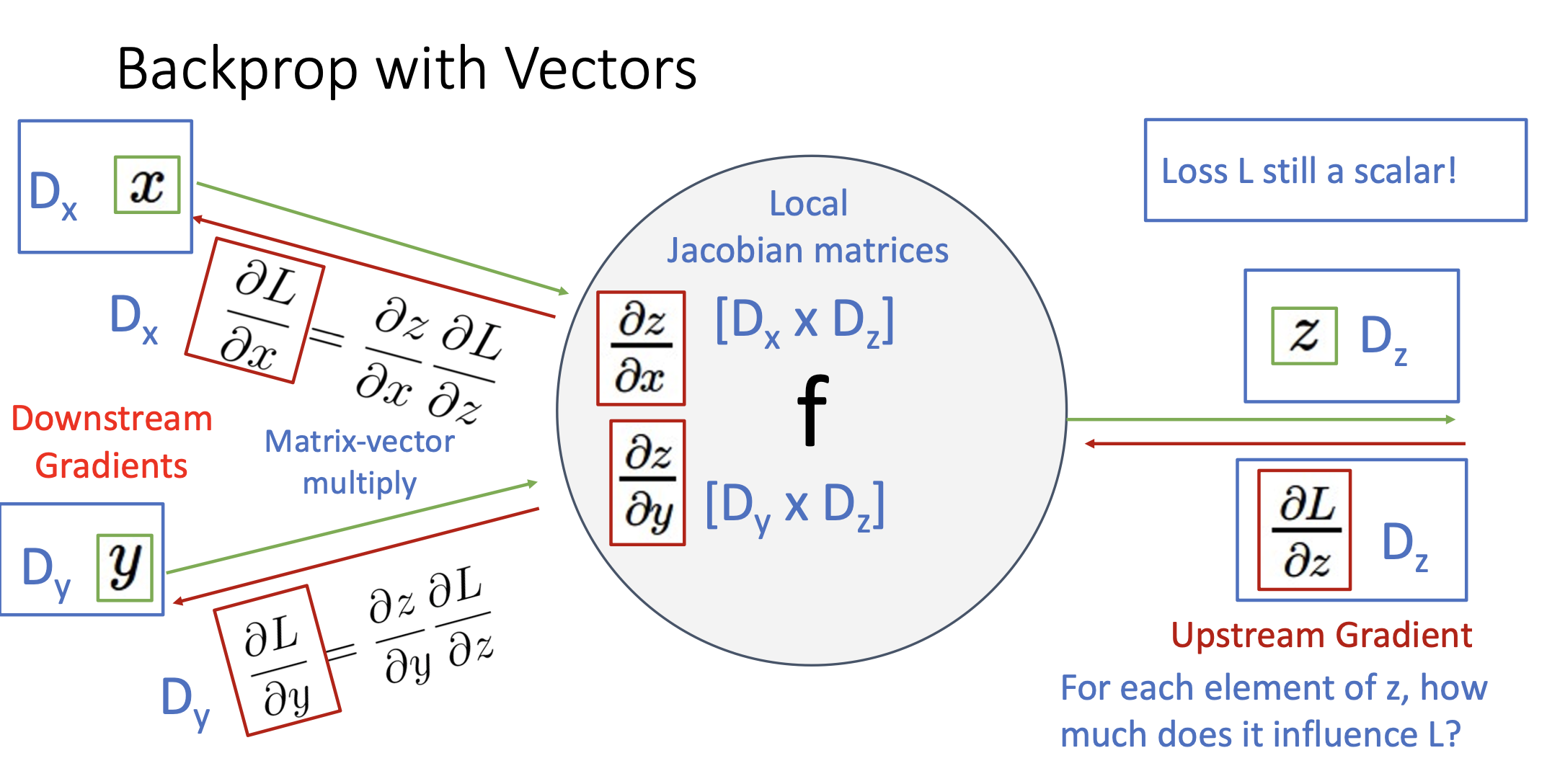
• Upstream Gradient: Vector
• Local Gradients: Jacobian Matrices
• Downstream Gradient: Vector (Jacobian Matrix * Gradient)

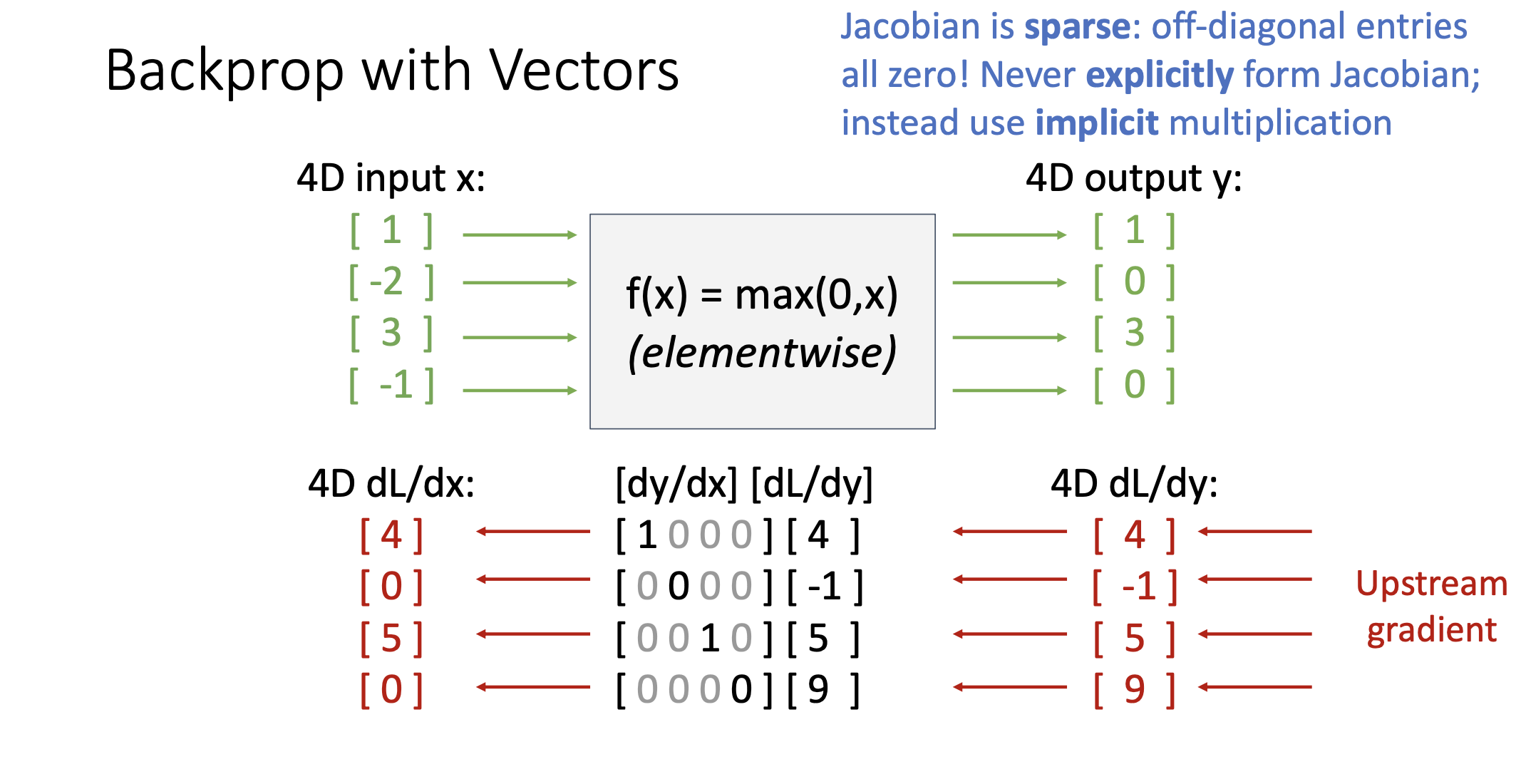
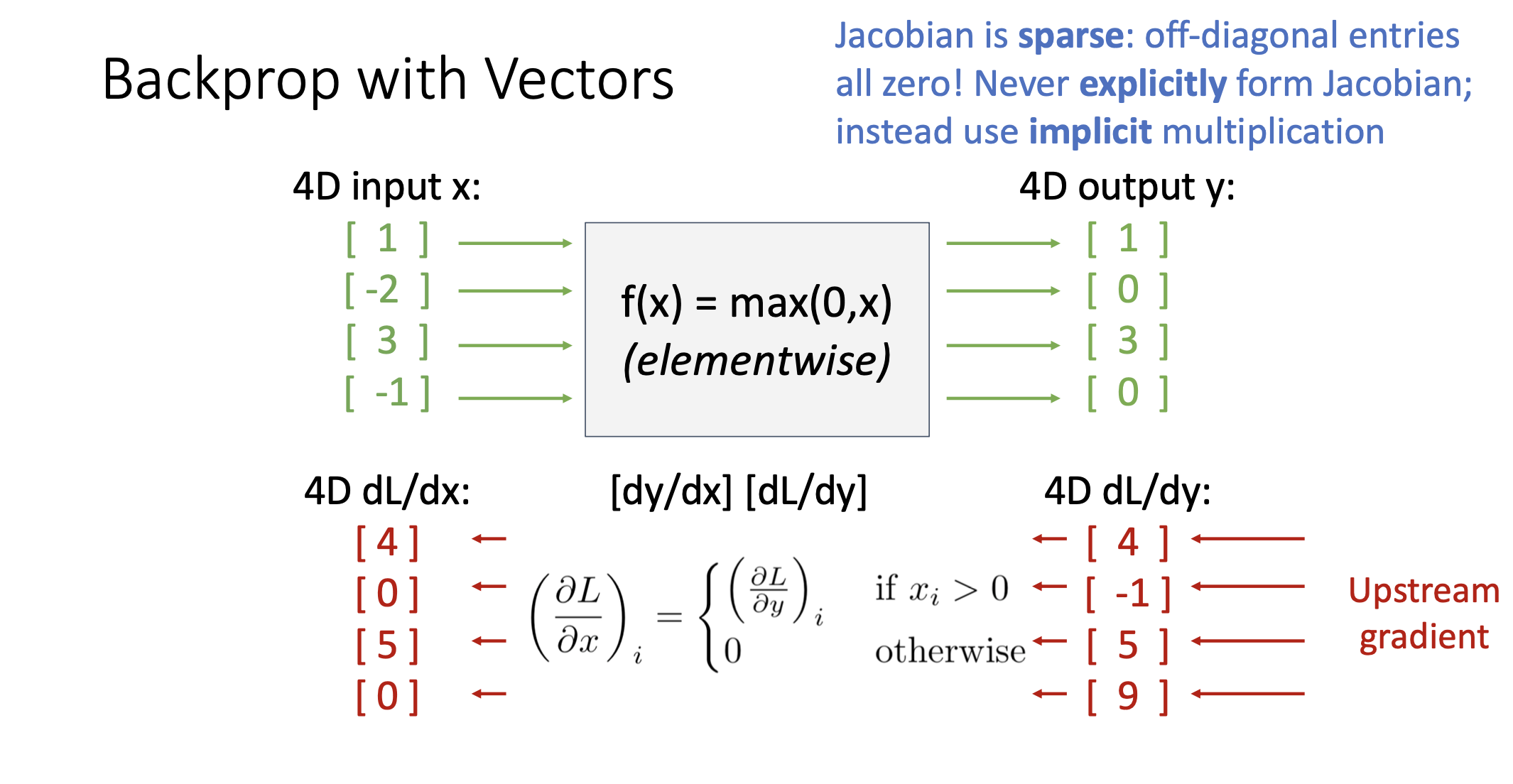
Backprop with Matrices

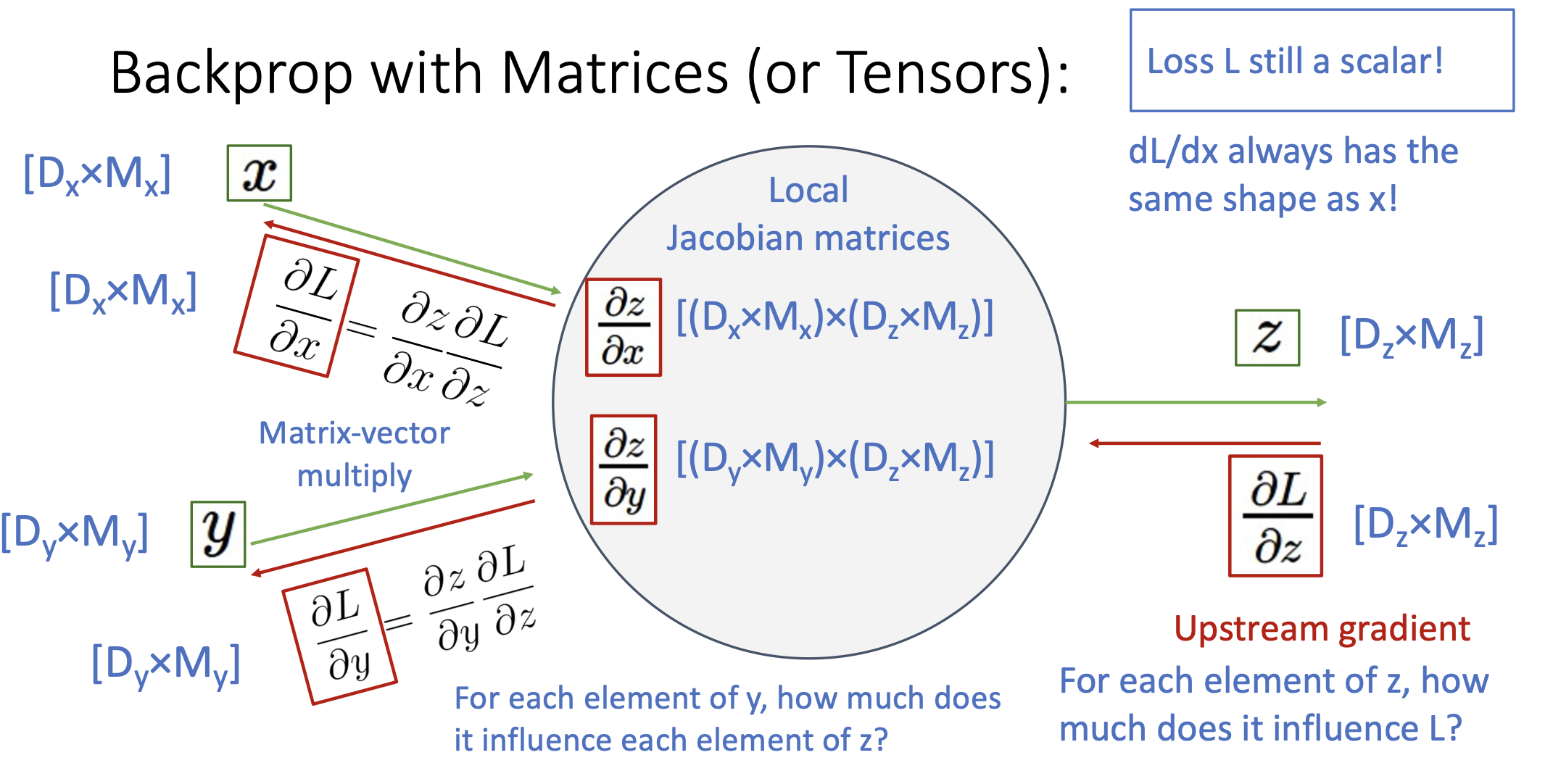
• Upstream Gradient: Matrix
• Local Gradients: Jacobian Matrices
• Downstream Gradient: Matrix (Jacobian Matrix * Matrix)

• 자코비안 행렬의 모든 값을 구하면 GPU 메모리를 넘어서게 되므로, Local Gradient Slice를 구하게 됨 (자코비안 행렬의 한 부분의 값)

• 자코비안의 한 값인 Local Gradient Slice를 구하고 dL/dx1,1 계산

• dL/dx(i,j)를 일반화하면
• dL/dx(i,j) = (w(j,:)) * (dL/dy(i:))

Reverse-Mode Automatic Differentiation

• 오른쪽에서 왼쪽으로 진행하는 계산은 matrix-vector 곱만을 필요로 함.
• Matrix-Matrix 연산을 피할 수 있음?

Forward-Mode Automatic Differentiation

• 순전파의 앞에 스칼라값을 넣고 왼쪽에서 오른쪽으로 연산
• 얘도 Matrix-Matrix 연산을 피할 수 있음?

Backprop: Higer-Order Derivatives

• 2차 이상의 미분을 본다는 의미
• Local Gradients 행렬로 자코비안 matrix 대신 Hessian matrix가 사용

gradient 가 주는 정보는 주어진 지점에서 tanhgent plane에 대한 정보를 주고,
H가 주는 정보는 특정 지점에서 local하게 얼마나 공유를 이루고 있는가에 대한 curvature정보를 준다. 2차 함수에서의 한번 미분하면 점선의 기울기과, 한번 더 미분하면 위로 볼록인지 아래로 볼록인지 판단가능하니까 이 때의 위로 아래로 볼록인지 여부가 curvature 정보이다.

참고) https://data-science-hi.tistory.com/115