Algorithm 

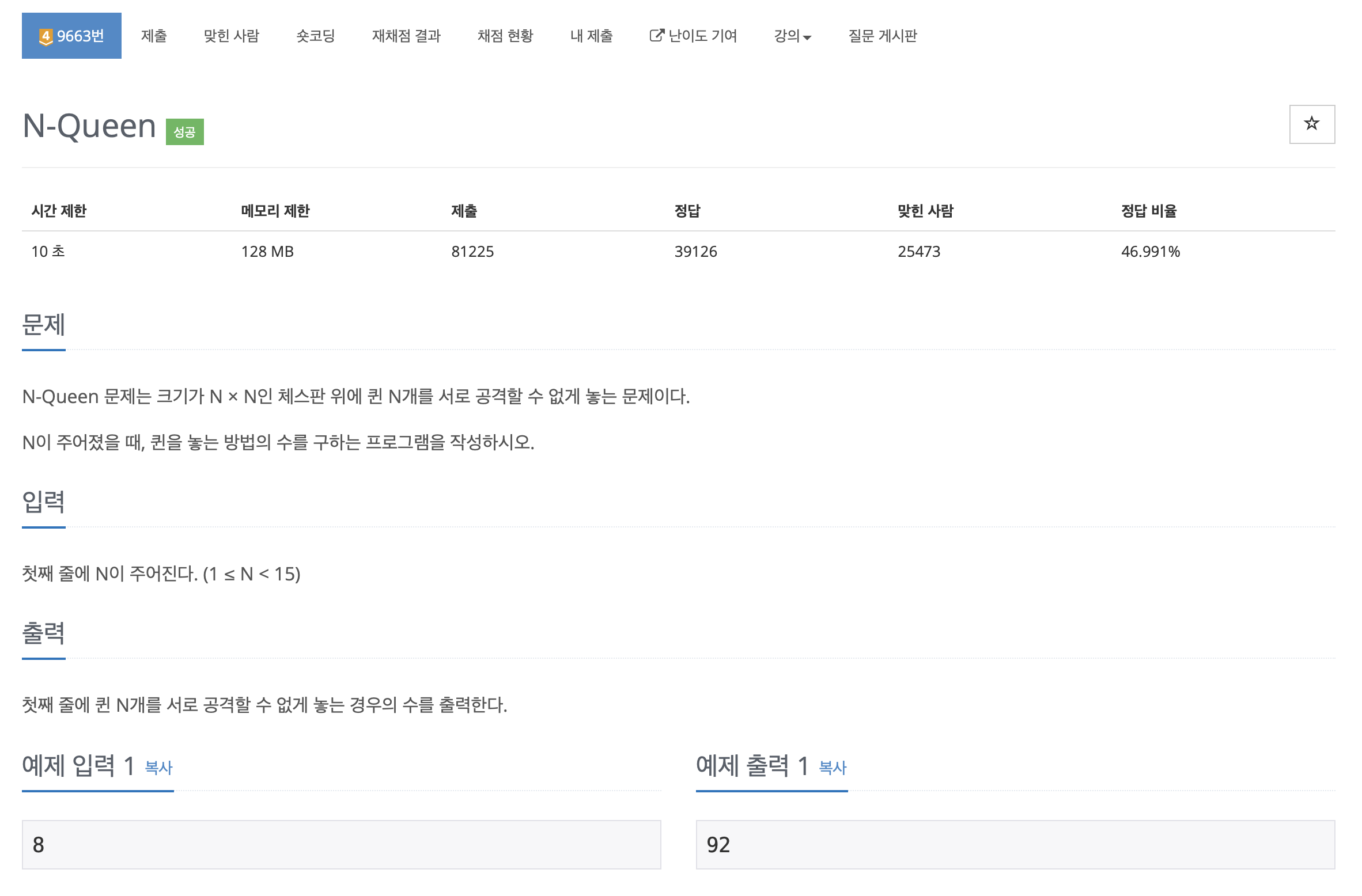
결론: N x N 판에 퀸 N개를 둘 수 있는 경우의 수를 구하라체스판은 행, 열로 이루어져 있다. → 2차원 배열을 써보자.퀸은 가로-세로-대각선 방향을 공격할 수 있다.→ 행-열에는 하나의 퀸만 존재할 수 있다.→ 다른 퀸과 행 번호와 열 번호의 차이값이 같으면 같

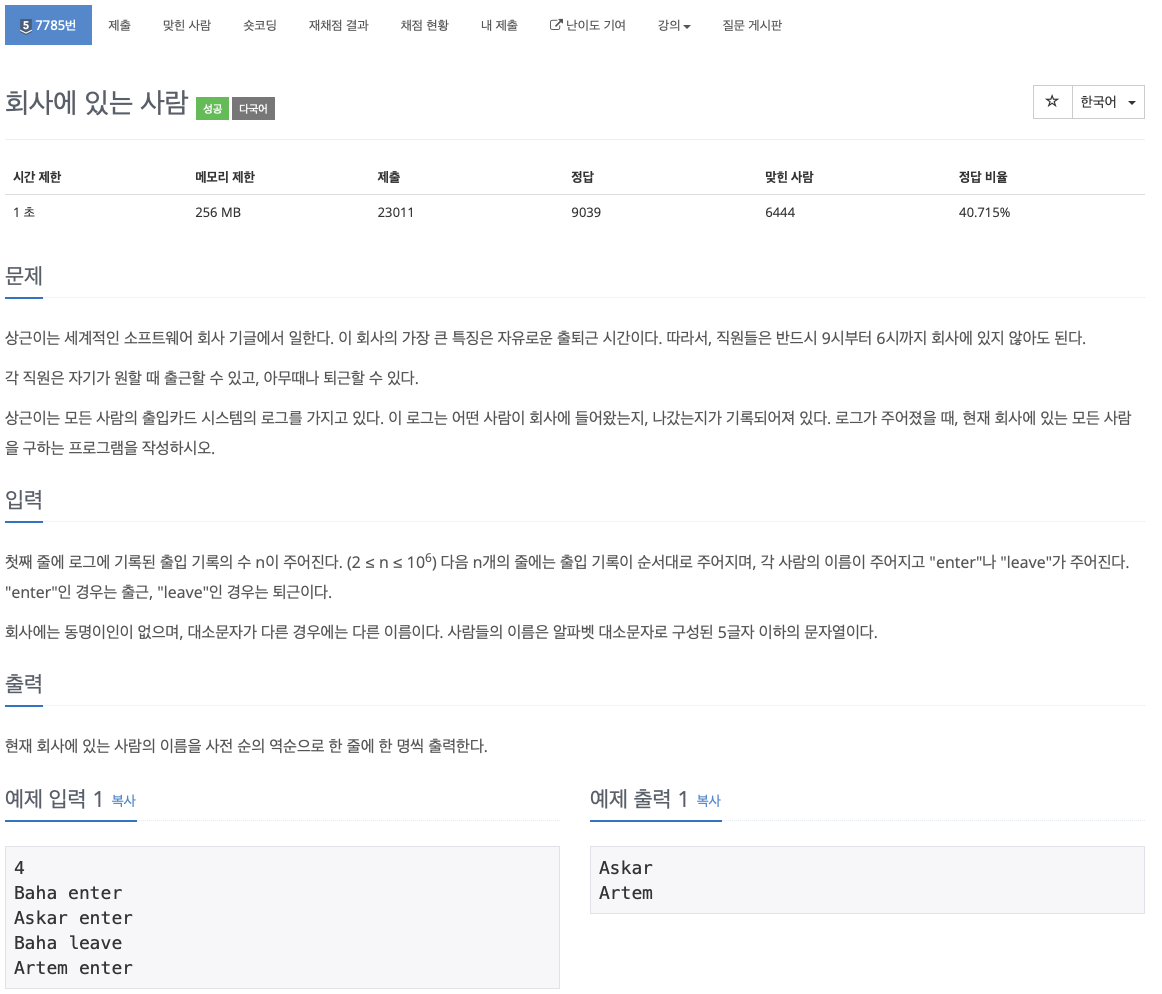
문제 재정의 및 추상화 > 결론: leave가 찍히지 않은 사람들의 목록을 사전 역순으로 구하라 문제 접근 방식 이름과 상태정보가 주어지는데, 정렬이 필요하다. -> 이름값을 기준으로 정렬하는 map을 이용해보자. 해법을 찾는데 결정적이었던 깨달음 📌 맵을 내림

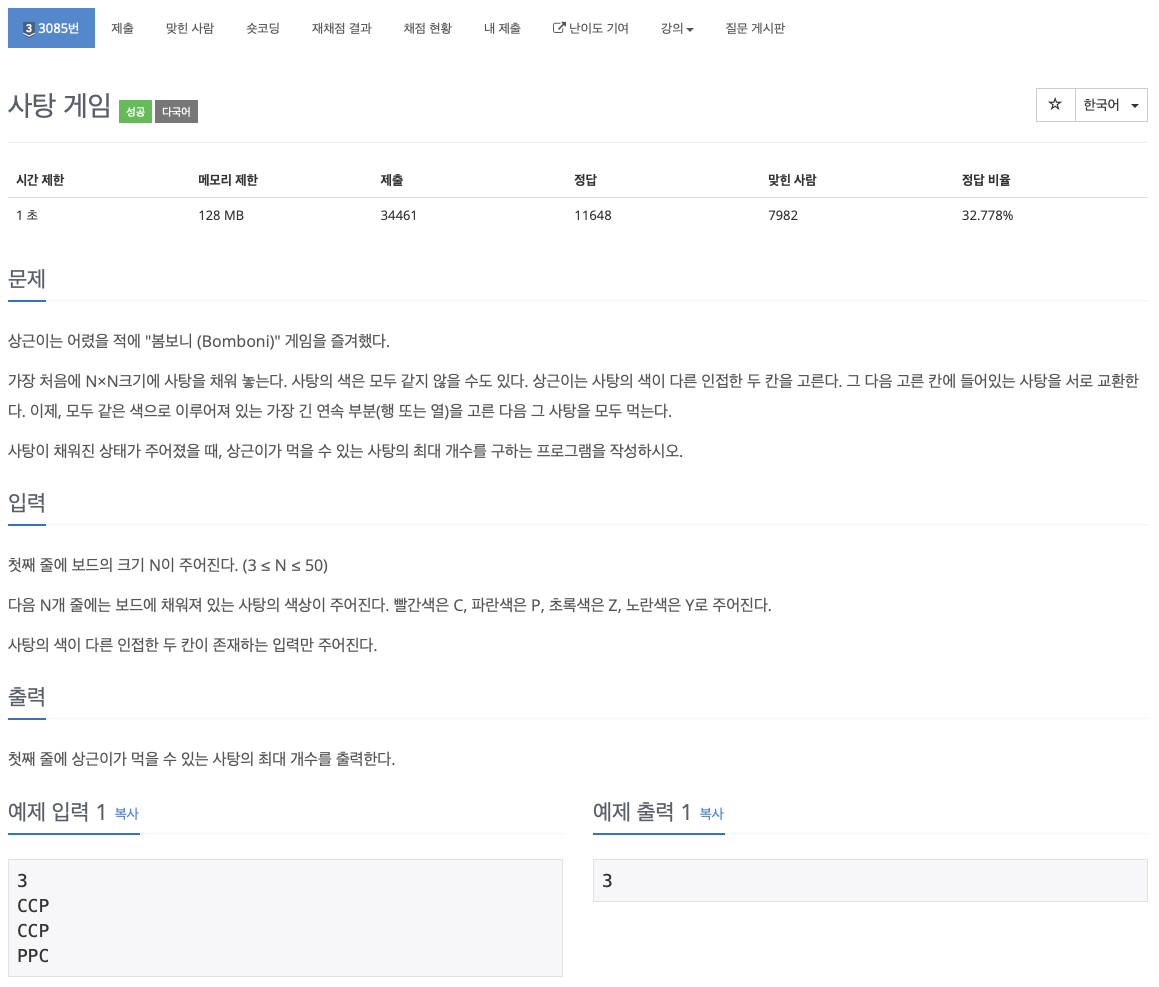
문제 재정의 및 추상화 > 결론: 행 또는 열을 기준으로 사탕을 하나씩 교환해보며 가장 긴 행이나 열의 사탕 개수를 구하라 쉽게 말하자면 애니팡 문제 접근 방식 행, 열 개념을 가진 N x N의 사탕 보드가 주어진다. -> 2차원 배열을 이용한다. 인접한 두 칸의

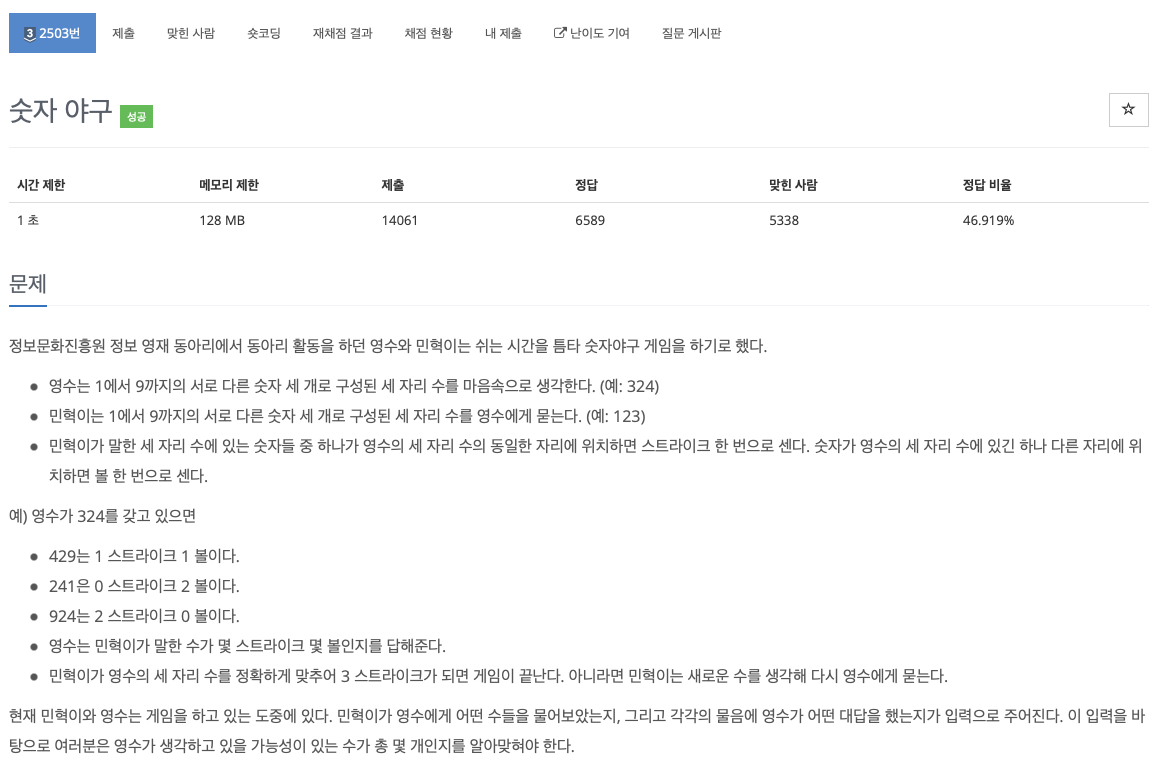
결론: 0과 중복 수를 허용하지 않는 숫자 게임에서 가능성 있는 답의 개수를 구하라.숫자만 같은 게 아니라 그 숫자의 자리도 중요하다\-> 인덱스 접근을 유용하게 하기 위해 문자열로 다뤄보자!📌 123~987 사이의 숫자를 담은 배열에 0과 중복을 제외하도록 답안지

결론: 주어진 수를 3으로 나누거나, 2로 나누거나, 1을 빼서 1로 만들 때, 최종 연산 횟수와 그 연산 과정에 있는 수들을 구하라.시간 제한은 매우 짧고, 계산 할 것은 매우 많다.\-> 동적 계획법을 써보자.백준에 있는 1로 만들기 문제와 같으나, 연산 과정에서

결론: 주어진 동전 종류로 주어진 금액을 만드는 경우의 수를 구하라작은 단위의 동전으로 해당 금액을 만드는 방법의 수는 계속 중복된다.\-> 계속 계산하지 말고 동적 계획법의 메모이제이션을 이용하자!📌 dpi = dpi + dpi - 동전 금액dp\[i] 는 i 원

문자열 검색 문제란 주어진 문자열 H가 문자열 N을 부분 문자열로 포함하는지 확인하고, 포함한다면 N과 일치하는 부분 문자열의 시작 위치를 찾는 문제르 말한다.이렇게 말하니 장황하지만 쉽게 말해 ctrl + f 를 구현하는 문제라고 할 수 있다.

깊이 우선 탐색은 말 그대로 깊이를 우선으로 하여 최대한 깊이 내려가며 탐색한 뒤 더이상 내려갈 곳이 없을 경우 옆으로 이동하며 탐색을 이어나가는 방법이다.이는 시작점이 되는 특정 노드에서 시작해서 해당 분기를 모두 탐색하고 다음 분기로 넘어가도록 탐색을 진행한다.경로

문제 재정의 및 추상화 > 결론: 문제 접근 방식 해법을 찾는데 결정적이었던 깨달음 📌 문제 풀이 로직 문제 풀이

결론: 중첩되는 합의 최솟값을 구하라앞 사람 시간이 짧을수록 전체 합이 작아진다.\-> 정렬 함수 sort 를 이용하자!📌 생각하는대로 풀면 된다. 최선의 값을 찾는 말 그대로 그리디!사람 수 n을 입력받는다.사람 수만큼 각 사람별로 걸리는 시간을 vector p에

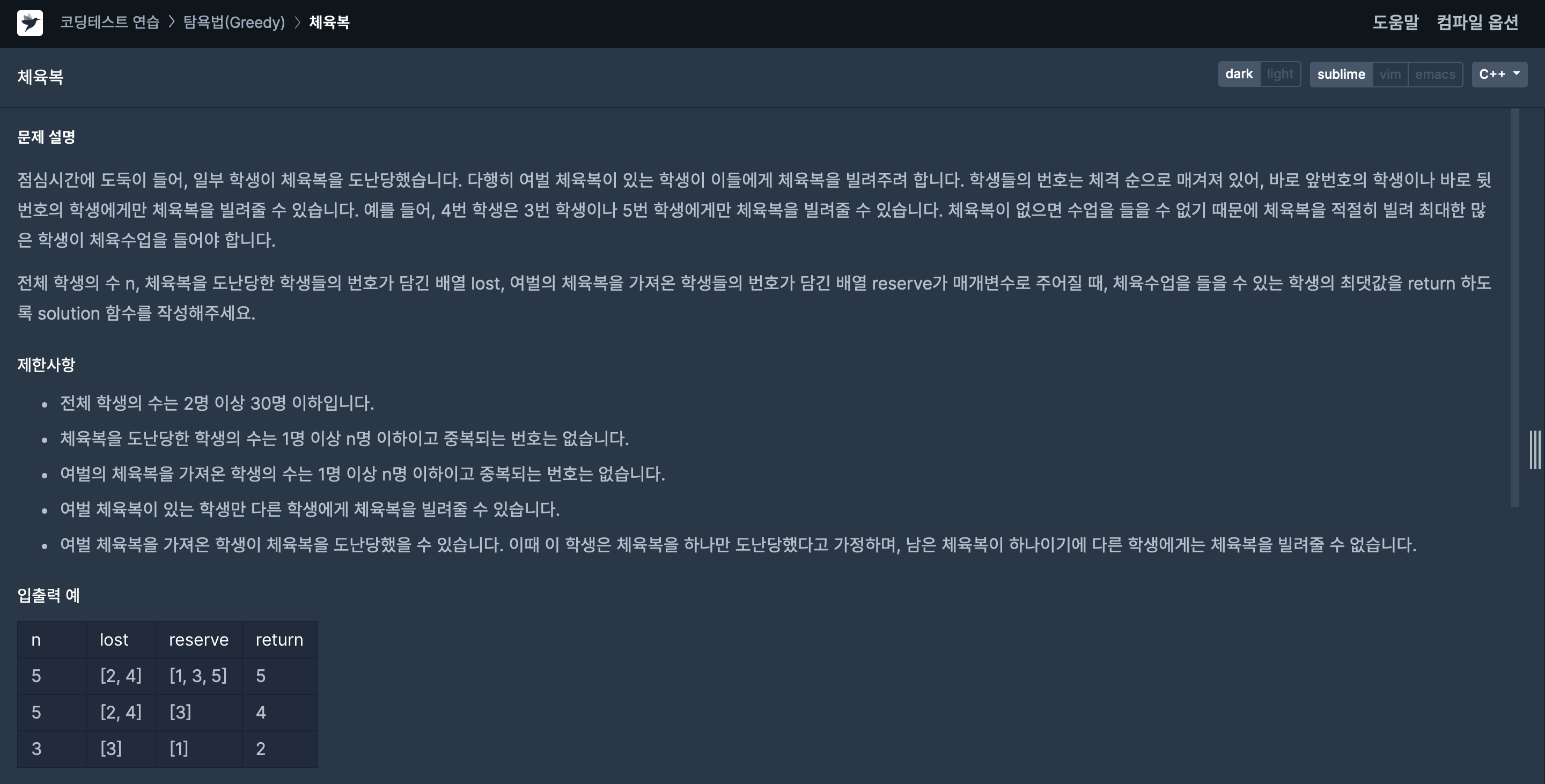
결론: 앞 뒤 번호끼리 서로 빌려줄 수 있을 만큼 빌려줘서 최대 인원이 체육복을 입게 하라체육복 개수에 대한 정보를 따로 저장해두자.\-> 학생에 대한 배열을 하나 새로 만든다!📌 학생들이 가진 체육복 개수는 -1(없음), 0(기본 상태), 1(여분 하나 더 있음)

결론: 수열에서 합이 0과 가장 가까운 두 수를 찾아라.음수와 양수가 존재할 수 있는 정렬된 수열에서 합을 구하므로 양쪽 끝에서부터 합을 구해본다.📌 같은 경우가 두 개 이상일 경우 그 중 아무것이나 하나를 출력한다고 했다.즉, 양쪽 끝에서부터 탐색하다가 0이 되는

문제 재정의 및 추상화 > 결론: 문제 접근 방식 해법을 찾는데 결정적이었던 깨달음 📌 나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 매우 크다!!(1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000) long long

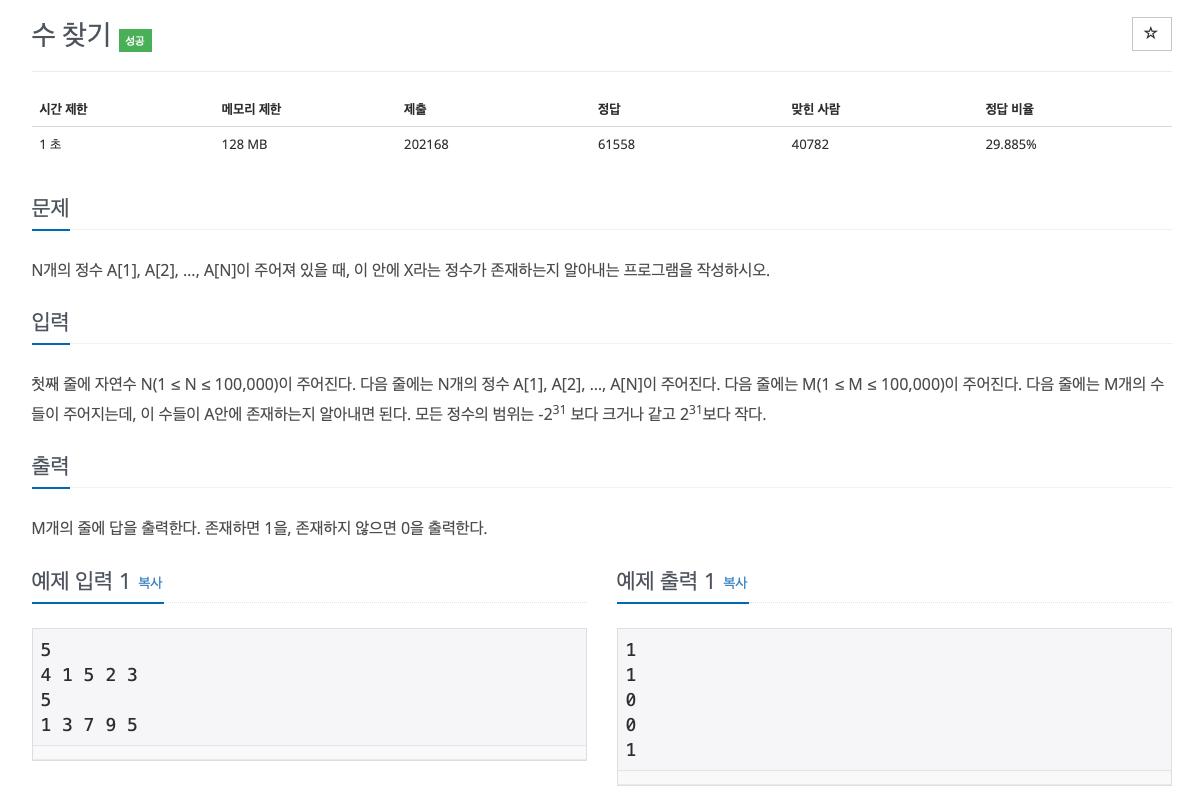
문제 재정의 및 추상화 > 결론: 문제 접근 방식 입력 수가 크므로 선형 탐색은 시간 초과가 날 수 있다. -> 이진 탐색을 써보자! 해법을 찾는데 결정적이었던 깨달음 📌 문제 풀이 로직 문제 풀이