[알고리즘 문제 해결 전략] KMP 알고리즘

akim·2023년 2월 1일

Algorithm

목록 보기

7/14

문자열 검색 문제란 주어진 문자열 H가 문자열 N을 부분 문자열로 포함하는지 확인하고, 포함한다면 N과 일치하는 부분 문자열의 시작 위치를 찾는 문제를 말한다.

이렇게 말하니 장황하지만 쉽게 말해 ctrl + f 를 구현하는 문제 라고 할 수 있다.

예를 들어 H = hogwarts , N = gwart 라고 한다면 H[2 ... 6] (앞으로 부분 문자열에 대한 표기를 이렇게 하도록 하겠다.) 이므로 H 는 N 을 포함하며, N 의 시작 위치는 2라고 할 수 있다.

이때 문자열 검색 알고리즘은 N 이 출현하는 모든 위치를 반환해야 한다.

여러 번 포함한다면 그 시작 위치를 모두 반환한다.

가장 간단하게 접근한다면...

이 문제를 푸는 가장 간단한 방법은 N 의 가능한 모든 시작 위치를 다 시도해 보는 것이다.

// H의 부분 문자열로 N이 출현하는 시작 위치들을 모두 반환한다.
vector<int> naiveSearch (const string& H, const string& N) {
	vector<int> ret;
	//모든 시작 위치를 다 시도해 본다.
	for(int begin = 0; begin + N.size() <= H.size() ; ++begin) {
		bool matched = true;
		for(int i = 0; i < N.size() ; ++i)
			if (H[begin + i] != N[il) {
			matched = false:
			break;
		}
		if (matched) ret.push_back(begin);
	}
	return ret;
}

처음에는 0번 글자에서 시작하는 부분 문자열이 N 과 같은지 확인하기 위해 H 와 N 의 글자를 하나하나 맞춰 나간다.
만약 모든 글자가 서로 일치한다면 이 위치를 답에 추가하고, 중간에 실패하거나 답을 하나 찾으면 시작 위치를 오른쪽으로 한 칸 옮겨 계속한다.

이 방법은 대부분의 위치에 대해 한 번 아니면 두 번의 비교로 불일치를 찾아낼 수 있기 때문에 충분히 효율적인 것처럼 보인다.

그러나 이 알고리즘은 특정 형태의 입력에 대해서는 매우 비효율적으로 동작한다.

예를 들어 H 와 N이 모두 a 로만 구성된 긴 문자열이라고 하면 이 경우 모든 시작 위치가 답이 된다. 그러나 위에서 살펴본 단순한 문자열 검색 알고리즘은 그걸 알 수 없기 때문에 |H| - |N| + 1 개의 모든 시작 위치에 대해서 비교를 수행한다. 대개 |H| >> |N| 이므로 시작 위치의 수는 O(|H|) 라고 할 수 있다.

각각의 비교에는 O(|N|) 의 시간이 걸리기 때문에, 이 알고리즘의 전체 시간 복잡도는 결국 O(|N| X |H|) 가 되는 것이다.

입력이 큰 경우 이 알고리즘은 이처럼 비효율적이라고 할 수 있지만, 그렇게 입력이 큰 경우는 흔하지 않으며 구현이 단순하다는 장점이 있기 때문에 이는 표준 라이브러리의 구현에 많이 쓰이는 방법이다.

C의 strstr() , C++의 string::find() , Jave의 indexOf() 등이 모두 이 알고리즘을 사용한다.

보지 않고도 알 수 있는 것이 있다: KMP 알고리즘

C++을 이용해서 알고리즘 문제 풀이를 하다보면 가끔 위에서 언급한 find() 를 쓸 일이 생기기도 한다. 그러나 이를 잘못 사용하면 시간 초과에 걸리기도 한다. 즉, 앞에서 말한 단순한 알고리즘이 우리가 만들 수 있는 최선의 알고리즘은 아니라는 의미이다.

검색 과정에서 얻는 정보를 버리지 않고 잘 활용한다면 많은 시간을 절약할 수 있다.

어떤 긴 문자열에서 N = "aabaabac" 를 찾는 경우를 예로 들어보자.

시작 위치 i 에서부터 N 을 맞춰 보니 첫 일곱 글자 aabaabac 는 모두 일치하고, 그 다음인 여덟 번째 글자부터 불일치가 발생했다면 위에서 본 단순한 알고리즘은 아 i는 답이 아니넹~ 하고 i + 1 위치로 넘어가 다시 답을 찾기 시작할 것이다.

그런데 생각해보면 조금 아깝지 않은가? ~~머가여?~~

약간의 탐색을 통해 지금까지 일곱 글자나 대응되었다는 엄청난 사실 을 알아내었는데 이를 그냥 버리고 다음 위치로 넘어간다니 엄청나게 아까운 일이다!

지금까지 몇 개의 글자가 대응되었다는 사실을 이용하면 우리는 시작 위치 중 일부는 답이 될 수 없을을 보지 않아도 알 수 있게 된다.

위치 i 에서 일곱 글자가 일치하기 위해서는 H 의 해당 부분 문자열인 H[i ... i+6] 이 "aabaaba" 이어야 한다.

그렇다면 i+1 에서 시작하는 N 은 H 와 일치할 수가 없다. N[1] 은 a인데 H의 대응하는 글자는 b임을 우리가 이미 알고 있기 때문이다.

이렇게 i+6 까지의 시작 위치를 하나하나 시도해 보면 답이 될 가능성이 있는 시작 위치는 i+3 과 i+6 밖에 없다는 것을 알 수 있다. 따라서 시작 위치를 i+3 으로 증가시키고 검색을 계속하면 된다.

이때 놀라운 것은 우리가 시작 위치 후보들을 걸러낼 때 쓴 정보는 오직 '현재 시작 위치에서 H 와 N 을 비교했을 때 몇 글자나 일치했는가' 뿐이며, 현재 H 내에서의 위치나 H 내에 포함된 문자들을 볼 필요도 없다는 것이다.

일치한 글자의 수는 항상 0에서 |N| 사이의 정수이기 때문에, 전처리 과정에서 이 정보들을 미리 계산해 저장해 둘 수 있다.

이와 같은 최적화를 적용한 문자열 검색 알고리즘을 커누스-모리스-프랫(Knuth-Morris-Pratt) 알고리즘 , 흔히 KMP 알고리즘 이라고 부른다.

다음 시작 위치 찾기

KMP 알고리즘은 앞에서도 설명했듯이, 불일치가 일어났을 때 지금까지 일치한 글자의 수를 이용해 다음으로 시도해야 할 시작 위치를 빠르게 찾아낸다.

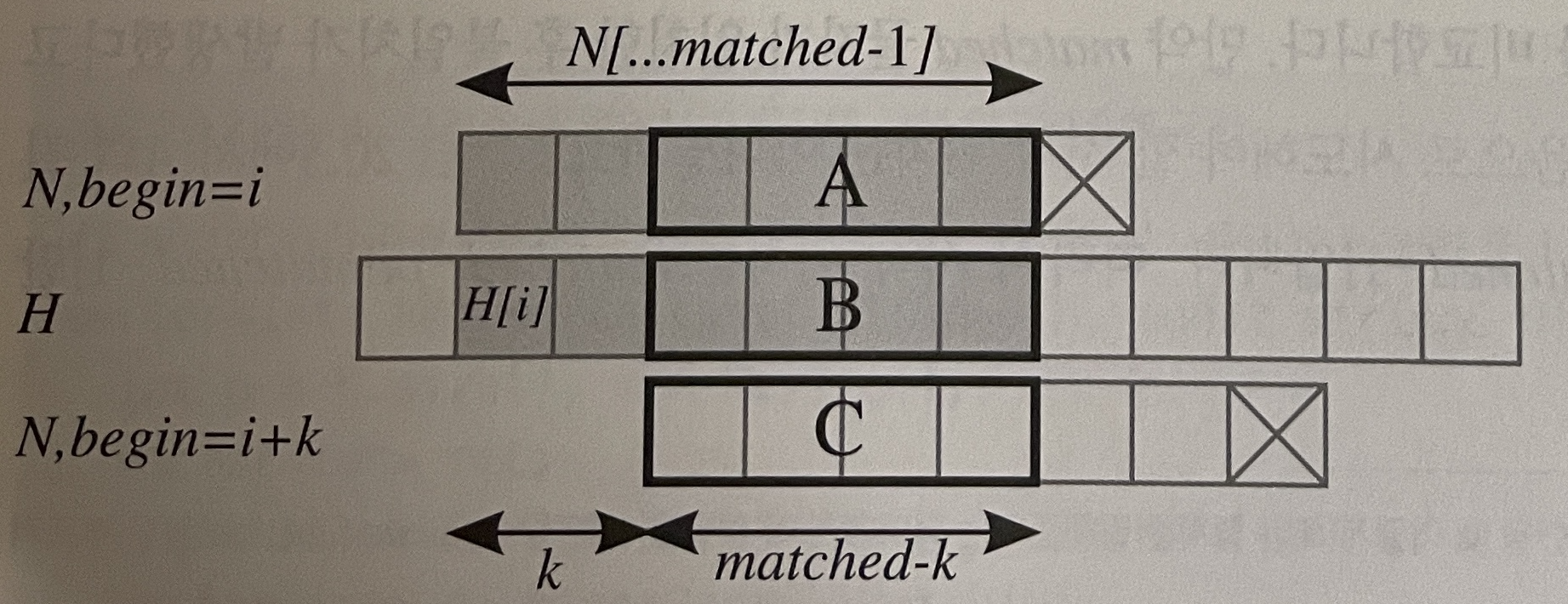
시작 위치 i에서도, 또 다른 위치 i+k 에서도 matched 글자가 일치하는 위 상황에서 박스 A = C 는 N[... matched - 1] 의 접두사이기도 하고 접미사이기도 해야 한다.

즉, 시작 위치를 i+k 로 하여 답을 찾을 수 있으려면 N[... matched - 1] 의 길이 matched - k 인 접두사와 접미사가 같아야 한다.

그러므로 답이 될 수 있는 바로 다음 위치를 찾기 위해서는N 의 각 접두사에 대해 접두사도 되고 접미사도 되는 문자열의 최대 길이를 계산해 두면 된다.

KMP 알고리즘은 전처리 과정에서 아래와 같이 정의되는 배열 pi[] 를 계산한다.

pi[i] = N[...i] 의 접두사도 되고 접미사도 되는 문자열의 최대 길이

pi[] 는 N 이 어디까지 일치했는지가 주어질 때 다음 시작 위치를 어디로 해야 할지를 말해 주기 때문에, 이를 흔히 부분 일치 테이블(partial match table) 이라고 부른다.

실제 문자열 검색의 구현

적절한 전처리 과정을 통해 pi[] 를 계산했다면 이제 진짜 문자열 검색을 수행할 준비를 마친 것이다.

KMP 알고리즘은 맨 처음에 보았던 단순한 알고리즘처럼 시작 위치 0에서부터 시작해서 H 와 N 의 글자를 비교한다.

📌 불일치가 일어나는 경우

만약 matched 글자가 일치한 후 불일치가 발생했다고 하면 다음으로 시도해야 할 시작 위치는 어디일까?

위 박스 그림에서 A의 길이가 pi[matched - 1] 이므로 시작 위치를 matched - pi[matched - 1] 만큼 증가시키면 된다.

여기서 깨달아야 할 중요한 점은 시작 위치를 움직인 후 첫 글자부터 다시 대응시켜 나갈 필요가 없다는 것이다.

새로운 위치에서 비교를 시작하더라도 N 의 첫 pi[matched - 1] 글자는 대응되는 H의 글자와 일치한다는 사실을 이미 알고 있기 때문이다. (위 그림에서 B와 C가 서로 같기 때문이다.)

따라서 matched 를 pi[matched - 1] 로 변경하고 비교를 계속하면 된다.

📌 답을 찾은 경우

그렇다면 답을 찾은 경우에는 어떻게 해야할까?

현재 시작 위치를 답의 목록에 우선 추가해야 한다는 것 빼고는 불일치가 발생한 경우와 똑같다. 그러고난 다음 답이 될 수 있는 다음 시작 위치에서부터 검색을 계속 이어나가면 된다.

그렇게 하여 KMP를 이용한 문자열 검색 알고리즘을 구현하면 아래와 같다.

// H의 부분 문자열로 N이 출현하는 시작 위치들을 모두 반환한다.
vector<int> kmpSearch (const string& H, const string& N) {
	int n = H.size(), m = N.size() ;
	vector<int> ret;
    
	// pi[i] = N[..i]의 접미사도 되고 접두사도 되는 문자열의 최대 길이
	vector<int> pi = getPartialMatch(N);
    
	// begin = matched = 0에서부터 시작
	int begin = 0, matched = 0;
	while (begin <= n - m) {
		// 만약 H의 해당 글자가 N의 해당 글자와 같다면
		if (matched < m && H[begin + matched] == N[matched]) {
			++matched;
			// 결과적으로 m글자가 모두 일치했다면 답에 추가한다.
			if (matched == m) ret.push_back(begin);
		}
		else {
			// 예외: matched가 0인 경우에는 다음 칸에서부터 계속
			if (matched == 0) ++begin;
			else {
				begin += matched - pi [matched-1];
				// begin을 옮겼다고 처음부터 다시 비교할 필요가 없다.
				// 옮긴 후에도 pi[matched-1]만큼은 항상 일치하기 때문이다.
				matched = pi [matched-1];
			}
		}
	}
	return ret;
}

문자열 비교가 실패했을 때 matched = 0 인 경우를 예외 처리한 것을 눈여겨보자.

한 글자도 일치하지 않고 (matched = 0 인 경우) 불일치가 발생했을 때 우리가 할 수 있는 일은 바로 다음 시작 위치에서 처음부터 검색을 재개하는 것 뿐이다.

부분 일치 테이블 생성하기

앞의 코드를 보면 getPartialMatch() 함수의 구현이 빠져있는 것을 볼 수 있다. 이제 이 함수를 어떻게 구현할지에 대해 알아보자.

📌 가장 간단한 방법 - O(|N|^3)

우선 이 함수를 구현하는 가장 간단한 방법은 N 의 각 접두사에 대해 가능한 답을 하나씩 모두 시도하는 것이다. 그러나 이 과정을 구현하면 각 접두사 길이의 제곱에 비례하는 시간이 걸리기 때문에, |N| 개의 모든 접두사에 대해 수행하려면 O(|N|^3) 의 시간이 걸린다.

📌 최적화를 한 번 거친 방법 - O(|N|^2)

이를 최적화할 수 있는 방법이 있다.

각 접두사에 대해 pi[] 의 값을 따로 계산하는 것이 아니라 모든 접두사에 대해 한꺼번에 계산하는 것이다.

두 글자 N[i] 와 N[begin + i] 가 일치할 때마다 pi[begin + i] 를 갱신해주면 단순한 문자열 검색에 걸리는 시간인 O(|N|^2) 만에 부분 일치 테이블을 계산할 수 있다.

이렇게 하면 단순한 문자열 검색을 구현했던 코드와 별로 달라진 게 없긴 하지만,

답을 찾을 가능성이 없더라도 [1, |N| - 1] 의 모든 시작 범위를 시도한다는 점
일치가 일어날 때마다 pi[] 를 갱신한다는 점

위 두 가지가 달라진다.

📌 KMP 알고리즘으로 구현하는 방법 - O(|N|)

그렇긴 하지만... 그래도... 기왕이면 이러한 검색 과정을 KMP 알고리즘으로 구현해보면 좋지 않을까?

처음에 생각한 문자열 검색과 거의 똑같긴 하지만 일치가 일어날 때마다 pi[] 를 갱신해주면 된다. 이 밖에도 눈여겨 볼 점이 몇 가지 있다.

begin 을 옮길 때 이전에 계산한 pi[] 값을 사용하고 있다.
현재 matched 글자가 일치했다면 pi[matched - 1] 은 항상 계산된 뒤임을 증명할 수 있기 때문이다.

pi[] 의 각 원소는 최대 한 번만 변경되기 때문에 O(|N|^2) 의 방법에 필요한 max() 연산을 따로 해 줄 필요가 없다.

이를 최종적으로 코드로 구현해보면 아래와 같다.

// N에서 자기 자신을 찾으면서 나타나는 부분 일치를 이용해 pi[]를 계산한다.
// pi[i] = N[..i]의 접미사도 되고 접두사도 되는 문자열의 최대 길이
vector<int> getPartialMatch (const string& N) {
	int m = N.size();
	vector<int> pi (m, 0);
 
	// KMP로 자기 자신을 찾는다.
	// N을 N에서 찾는다. begin = 0이면 자기 자신을 찾아버리니까 안됨!
	int begin = 1, matched = 0;
	
    //비교할 문자가 N의 끝에 도달할 때까지 찾으면서 부분 일치를 모두 기록한다.
	while (begin + matched < m) {
		if (N[begin + matched] == N[matched]) {
			++matched;
			pi[begin+matched-1] = matched;
    	}
		else {
			if (matched == 0) ++begin;
			else {
				begin += matched - pi [matched-1];
				matched = pi[matched-1];
			}
		}
	}
	return pi;
}