통계적 가설 검정 : 표본에서 얻은 사실을 근거로 하여 모집단에 대한 가설이 맞는지 통계적으로 검정하는 분석방법
- 가설을 먼저 세워야 됨.
- 귀무가설 (H0) : 검정대상이 되는 가설. 기존에 일반적인 사실로 받아들여지고 있는 내용을 나타내는 가설
- 대립가설 (H1) : 연구자가 새로이 주장하여 검정하고자 하는 가설
귀무가설의 기각(Reject)를 목표로 함.
가설검정 예시
대한민국 남성 100명을 대상으로 키를 sampling했을 때 표본평균 = 173이 나왔다고 하자.
대한민국 남성 키가 모표준편차가 12인 경우 170cm 이상이라고 할 수 있는지 알아볼 수 있는 가설은
H0 : μ = 170, H1: μ > 170 이라고 하
-
유의수준 : 귀무가설이 실제로 옮음에도 기각하는 오류
즉, 귀무가설이 실제로는 맞지만 틀리다고 할 수 있는 확률, 위험부담이라고 함.
보통 0.05로 값을 설정 -
임계값 : 유의수준이 주어졌을 때 귀무가설의 채택과 기각 의사를 결정하는 기준이 되는 값
-
표준 정규분포표를 이용해 (1-a)=0.95에 해당하는 값을 찾으면
z=1.645(H1 : μ != 170이 아닌 μ > 170 이므로 단측검정이다.)
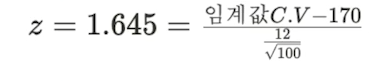
임계값 C.V는 약 171.974가 된다.
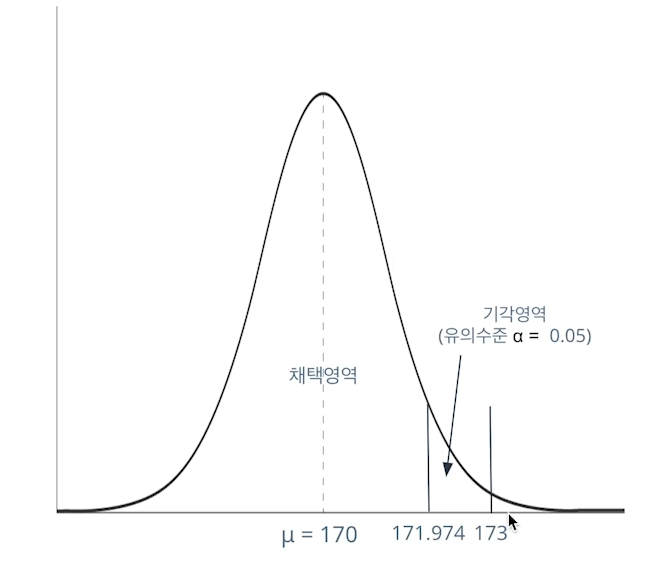
임계값 171.974를 기준으로 표본평균은 173, 임계값보다 크다. (채택영역에 들어오지 못함)
따라서 귀무가설은 기각되고, 대립가설이 채택된다.
즉, 대한민국 남자의 평균 키는 170cm 이상이라고 할 수 있다단, 대립가설은 ‘귀무가설이 기각되었기 때문에 채택되었다’ 라고 이야기 되어야 한다.
즉, 대립가설이 참이라서가 아닌 다른 이유들로 귀무가설이 기각 되었다는 것을 항상 기억해야된다.
-
가설검정의 오류
- 1종 오류 (LEVEL 1 오류) : 귀무가설이 참임에도 이를 기각하는 오류
- 2종 오류 (LEVEL2 오류) : 귀무가설이 거짓임에도 이를 채택하는 오류
보통 2종 오류가 더 위험하다.

