데브코스_데이터분석-데이터 분석 과정 학습 및 시각화 실습(1)[7주차]
1.[31일차]데이터 분석이란?
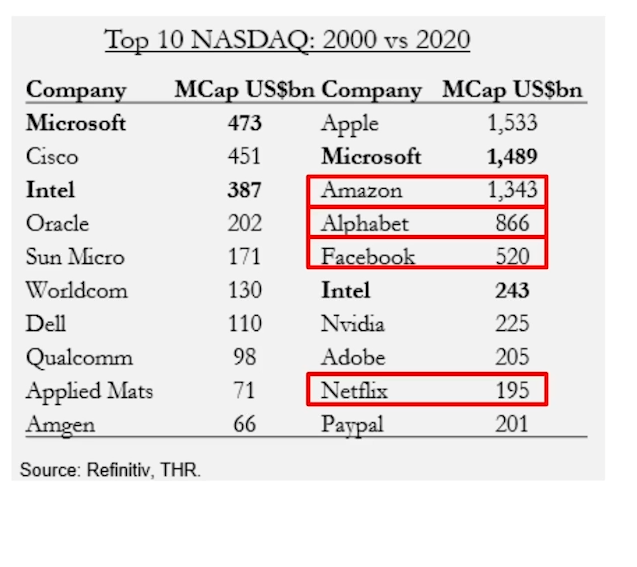
2000년 VS 2020년 NASDAQ 시총 상위 기업을 보면‘제조업’ 기업 → ‘서비스’ 기업 으로 이동하는 것을 볼 수 있다.FAANG(페이스북, 아마존, 애플, 넷플릭스, 구글) 중 애플을 제외한 모든 기업은 제조업이 아닌서비스 기업이들은 도대체 무엇을 판매하여
2.[31일차]데이터 분석 과정
문제 정의데이터 수집데이터 전처리데이터 분석데이터 분석에서 나온 인사이트 리포팅 / 피드백풀고자 하는 문제가 명확하지 않으면 데이터 분석은 무용지물이다.문제정의시 생각해야 될 것.궁극적으로 해결하고자 하는 문제(달성하고자 하는 목표)해당 문제를 일으키는 원인이 무엇인가
3.[31일차]데이터 분석 툴(Google colab) 소개

Colab은 클라우드 기반의 Jupyter 노트북 개발 환경이다.웹 브라우저에서 텍스트와 프로그램 코드를 자유롭게 작성할 수 있는 일종의 온라인 텍스트 에디터이다.CPU와 램을 제공해주기 때문에 컴퓨터 성능과 상관없이 프로그램을 실습할 수 있다.아이패드로도 가능!Col
4.[31일차]데이터 정규화와 스케일링 기법
데이터에서 하나의 instance(sample)는 그것이 가진 여러 속성값들을 이용해서 표현이 가능하다.이 속성값들을 feature라고 한다.(e.g. 엑셀 테이블에서 row는 sample, column은 sample들이 가지는 속성값을 의미)feature들간의 크기
5.[31일차]스케일링 실습
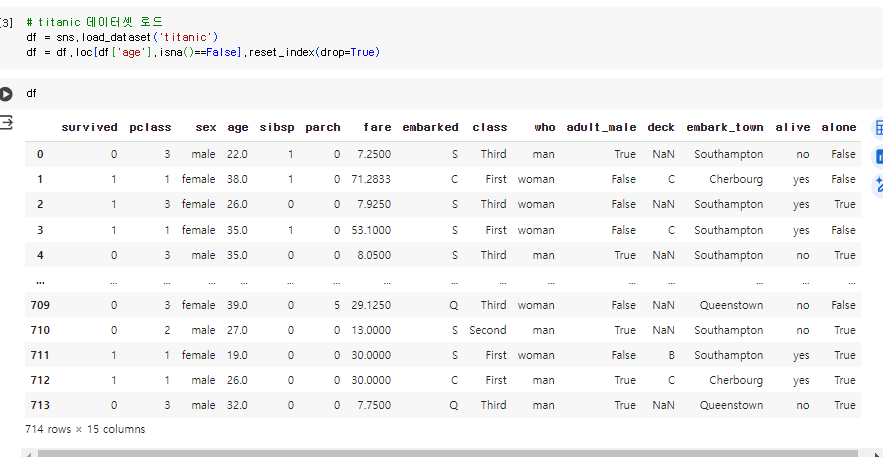
스케일링 실습은데이터 시각화 부분은 numpy, pandas, seaborn 라이브러리를 사용할 것 이다.numpy :파이썬의 기본 데이터 구조인 리스트와 배열과는 다르게, 고성능의 다차원 배열 객체와 이를 처리하기 위한 도구를 제공pandas :데이터 조작 및 분석을
6.[32일차]확률과 확률 변수

32일차 스포를 좀 하자면...1학년때 통계를 함축하고 또 다른 지식을 알려주셨다...ㄹㅈㄷ...여러 사건들을 수학적으로 모델링하고, 이를 분석하는 것이 통계학의 본질사건은 근본적으로 발생하기 전에는 알 수 없으므로 불확실성을 내포하고있다.이러한 불확실성을 표현할 수
7.[32일차]확률 분포
확률 분포확률 변수의 모든 값과 그 확률이 어떻게 분포하는지를 의미e.g. X=동전을 두번 던져서 앞이 나오는 확률 변수 일때 X가 가질 수 있는 값 = {0,1,2} 한번 도 안나올 확률, 한번만 나올 확률, 둘다 나올 확률 확률 분포는 확률 함수확률 변수 X를
8.[32일차]확률 함수
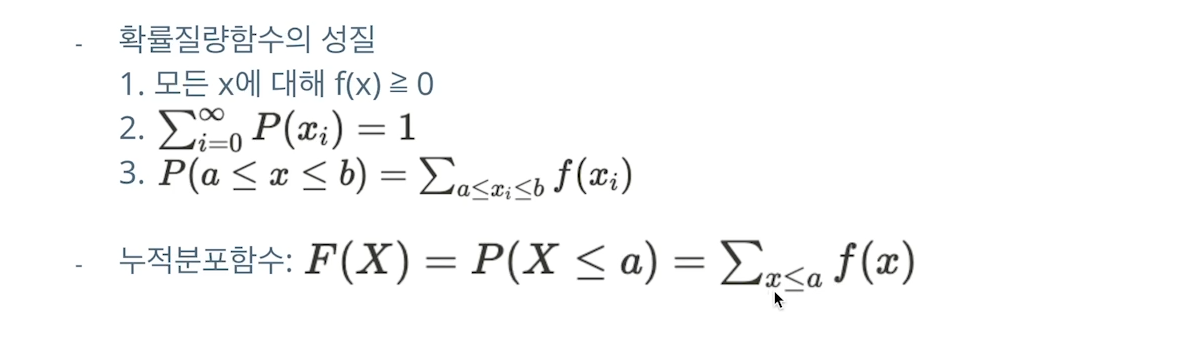
확률질량함수(PMF,Probability Mass Function)이산확률변수 X가 취할 수 있는 값 x0, x1, …의 각각에 대해확률값 P(X=x0), P(X=x1), … 를 대응시켜주는확률함수를 X의 확률질량함수 f(x)라고한다.확률질량함수의 성질음수는 될 수 없
9.[32일차]모집단,모수,표본

통계학에서 관심의 대상이 되는 모든 개체 값의 집합e.g. “대한민국 고등학생의 평균 키를 알고싶다.”이때 모집단 : 대한민국의 ‘모든’ 고등학생들의 키 값모집단의 특성을 나타내는 통계적인 특성치e.g. 모집단이 정규분포를 따른다고 할 때,모집단의 분포 특성을 나타내는
10.[32일차]확률분포
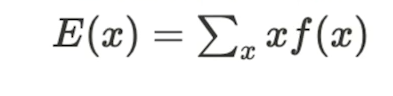
기댓값 : 어떤 확률적 사건이 평균적으로 가질 수 있는 값(=평균값,E(x), μ 모집단의 기댓값)이산확률변수의 기댓값: 모든 확률변수에 대해서 값에 xf(x)를 곱하면 기댓값이 나옴.연속확률변수의 기댓값: -무한대~무한대의 확률값을 더함. 이때 적분을 진행기댓값의 성
11.[32일차]공분산
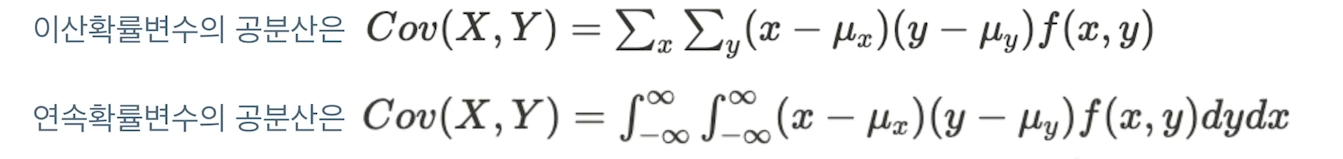
공분산 : 두 개의 확률변수 X와 Y에 대해 X가 변할 때 Y가 변하는 정도를 나타내는 값즉, X와 Y가 같이 변하는 정도를 나타내는 값Cov(X, Y) = E(X-μX)(Y-μY), 편차의 곱의 기댓값이 때 (X-μX), (Y-μY)를 편차라 합니다 기대값의 성질(E
12.[32일차]베르누이분포, 이항분포
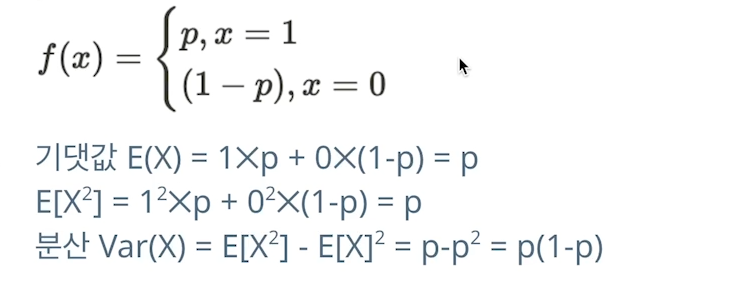
앞에서 배운 통계값에 대해 만드는 분포를 알아보자베르누이 시행 : 어떤 시행의 결과가 1(성공) or 0(실패)인 실험베르누이 시행에서 확률변수 X=1일 확률이 p, X=0일 확률이 q=1-p인경우확률변수 X는 베르누이 분포를 따른다고 볼 수 있다.pmf는 식만 보면
13.[32일차]포아송분포, 균등분포
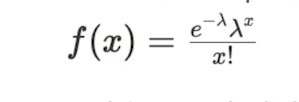
단위시간/단위공간에서 어떤 사건이 발생하는 횟수를 확률변수 X라 할때, X는 포아송 분포를 따른다고 한다.포아송 분포에서 모수 λ(람다)는 ‘단위시간/단위공간에서의’ 평균 발생 횟수e.g. 1시간 동안 버스가 정류장에 도착하는 횟수포아송 분포의 전제조건독립성 : 단위
14.[32일차]정규분포⭐
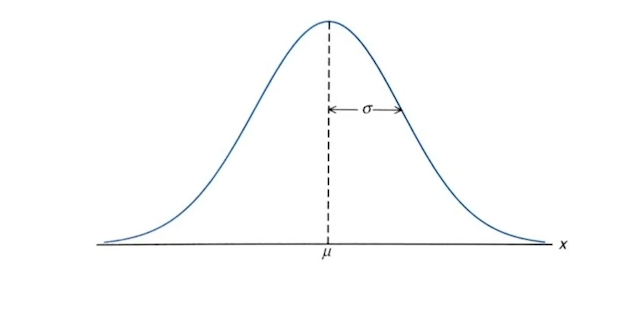
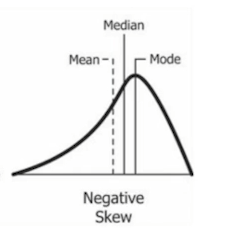
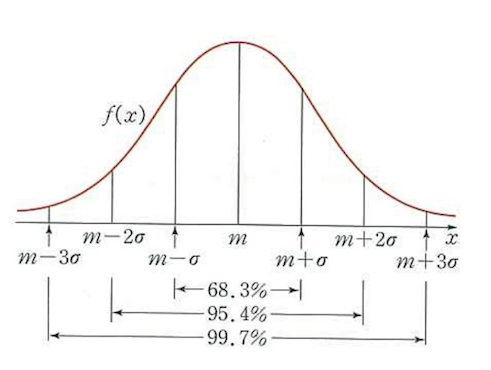
정규분포가장 일반적으로 발견되는 양방향 대칭의 종 모양(사진 참고)으로 생긴 분포,수집된 자료의 분포를 근사할 때 대부분 정규분포를 사용한다.(중심 극한정리에 의해 독립적인 확률 변수들의 평균이 정규분포에 가까워지므로) 모수: μ(평균)과 σ^2(분산)평균: 분포가 모
15.[32일차]기술통계
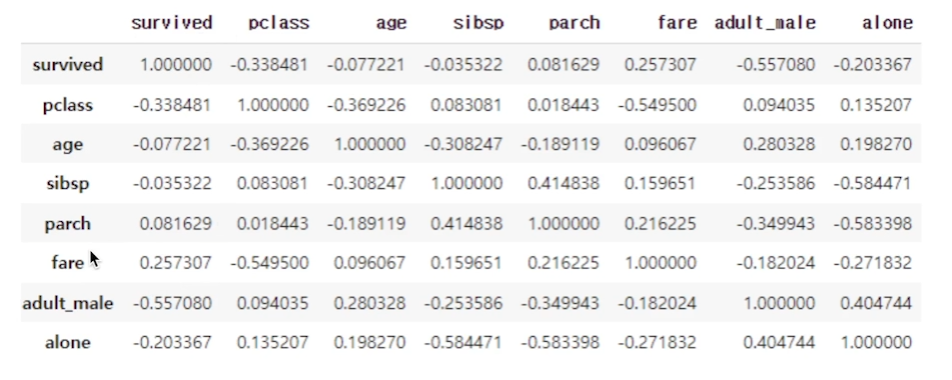
이번 글에서는 파이썬을 통해 기술통계를 진행하는 방법을 알아볼 것 이다.정량적 데이터 분석은 숫자로 표현되는 수치 데이터를 이용하여주어진 데이터를 분석하는 과정통계 수치를 구하여 이 값으로부터 여러 정보를 발견해내며,다음과 같은 통계 수치를 주로 활용한다. \-
16.[32일차]가설검정

통계적 추정 : 모집단의 모수θ를 표본들의 통계값을 이용해서 추정하는 방법점추정 : 모집단의 특성을 단일한 값으로 추정이때 점추정값 θ^은 표본값 X1,…,Xn 들의 함수이다.평향 : 추정량의 기댓값과 모수의 차이 (E(θ^)-θ)평균제곱오차 : E(θ^-θ)^2편차의
17.[32일차]구간추정

점추정량은 추정된 값이 실제 모수와 얼마나 가까운지 사실 알 수 없다.구간추정 : 모수가 있을 것으로 예상되는 구간을 정해놓고, 해당 구간에 실제 모수가 있을 것으로 예상되는 확률을 구하는 것신뢰도 : 설정한 구간에 실제로 모수θ가 있을 확률예시) 확률구간a,b에 대해
18.[32일차]t분포,F분포
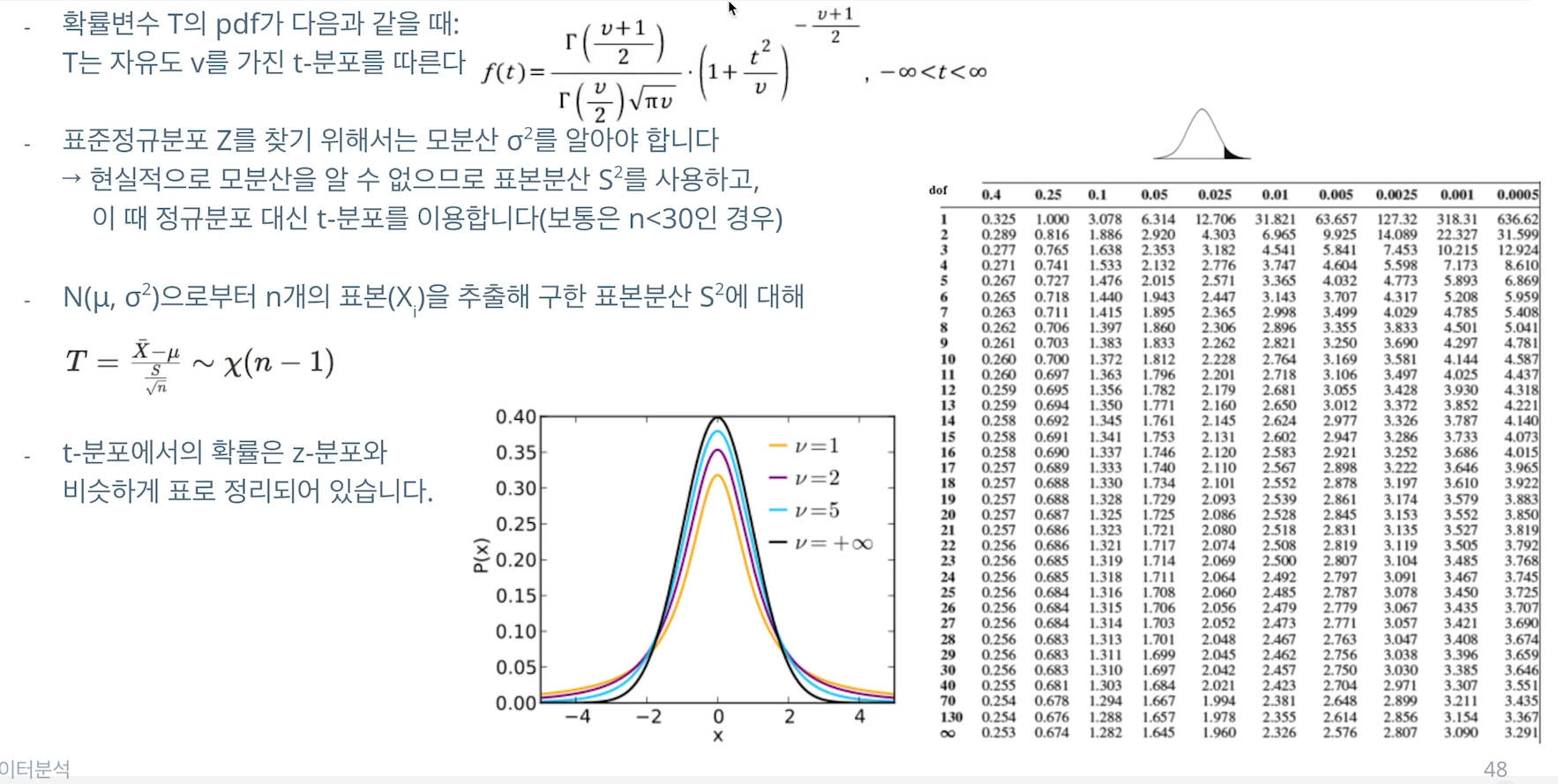
F-분포 :서로 독립인 두 확률변수 U와 V가 각각 자유도가 v1, v2인 카이제곱 분포를 따를 때, 새로운 확률 변수 F = (U/v1)/(V/v2)는 자유도가 (v1,v2)인 F-분포를 따른다.정규분포를 이루는 모집단에서 독립적으로 추출한 표본들의 분산 비율을 나
19.[32일차]모평균 구간추정

업로드중..
20.[32일차]모분산,모비율 구간추정

21.[32일차]가설검정 - 귀무가설, 대립가설
통계적 가설 검정 : 표본에서 얻은 사실을 근거로 하여 모집단에 대한 가설이 맞는지 통계적으로 검정하는 분석방법가설을 먼저 세워야 됨.귀무가설 (H0) : 검정대상이 되는 가설. 기존에 일반적인 사실로 받아들여지고 있는 내용을 나타내는 가설대립가설 (H1) : 연구자가
22.[32일차]단측검정, 양측검정

H1, H0을 어떻게 지정하냐에 따라 검정 방법이 달라진다.
23.[32일차]모평균,모분산 가설검정

모평균의 구간 추정과 같이 모분산을 아는 경우와 모르는 경우로 나눠서 접근한다.
24.[32일차]ANOVA
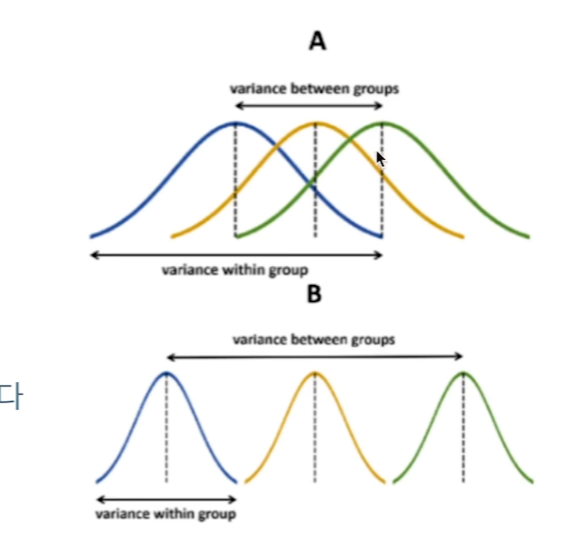
AVOVA : n개의 집단을 비교하는 통계적 분석(n>2)n>2인 경우 n개의 집단에서 t 검정을 하는 경우 문제 발생e.g. n개의 집단에서 한번이라도 type 1 error가 발생할 확률 = 1-0.95^n>0.05즉, type 1 error의 누적을 해결하기 위해
25.[33일차]matplotlib의 기본문법
\*\*matplotlib\*\*은 다양한 데이터를 많은 방법으로 도식화 할 수 있도록 하는 파이썬 라이브러리로써, 우리는 \*\*matplotlib\*\*의 pyplot을 이용하게 된다.\*\*matplotlib\*\*을 이용하면 numpy나 pandas에서 사용되는
26.[33일차]matplotlib plot의 종류 - Scatterplot, Barplot, Histogram
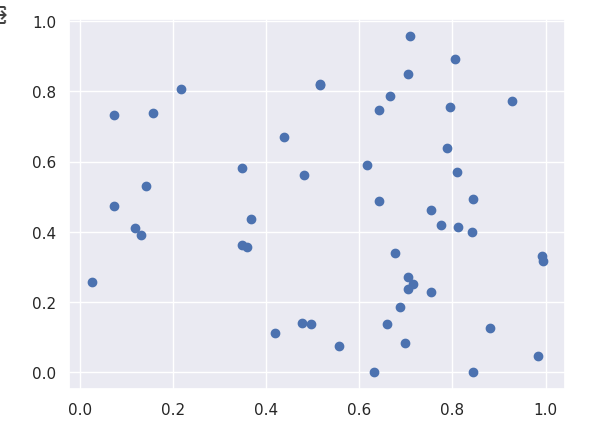
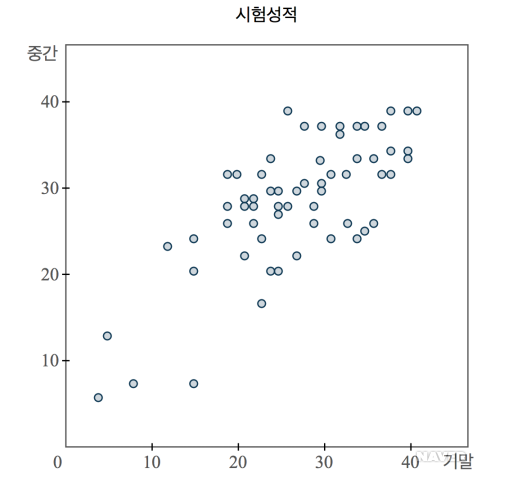
실제로 matplotlib.pyplot 에서 사용하는 플롯의 종류를 알아보자산점도는 데이터가 어떤식으로 분포되어있는지 확인할 때 유용하다.plt.scatter(s=,c=)x,y좌표로 이뤄진 데이터들을 점으로 표현하는 플롯s= 점 크기, c= 점 색깔을 조절하며lable
27.[33일차]matplotlib plot의 종류 - Piechart, heatmap
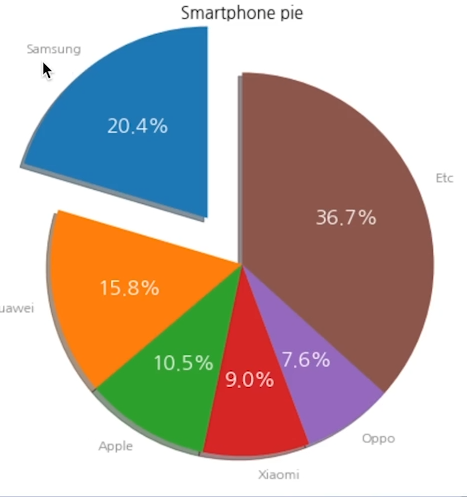
plt.pie() 를 이용해 위의 원 그래프를 만들어보자plt.pie() 인자값explode= : 파이에서 툭 튀어져 나온 비율(위에서 삼성과 같이)autopct= 퍼센트 표기‘%.1f%%’ : 소수점 1자리까지 표기shadow : 그림자 표시startangle :
28.[33일차]matplotlib plot의 종류 - Colormaps
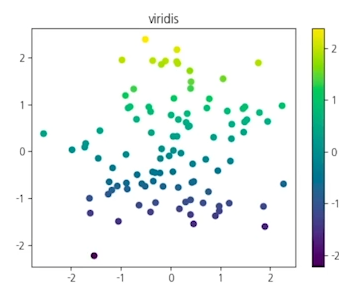
위와 같이 생긴 플롯을 컬러맵이라고 한다.matplotlib.pyplot 모듈은 컬러맵을 간편하게 설정하기 위한 여러 함수를 제공한다.plt.viridis(),plt.plasma(),plt.jet() 와 같은 함수를 이용해서 여러가지 색깔을 만들 수 있음.컬러맵을 만
29.[33일차]matplotlib plot의 종류 - style
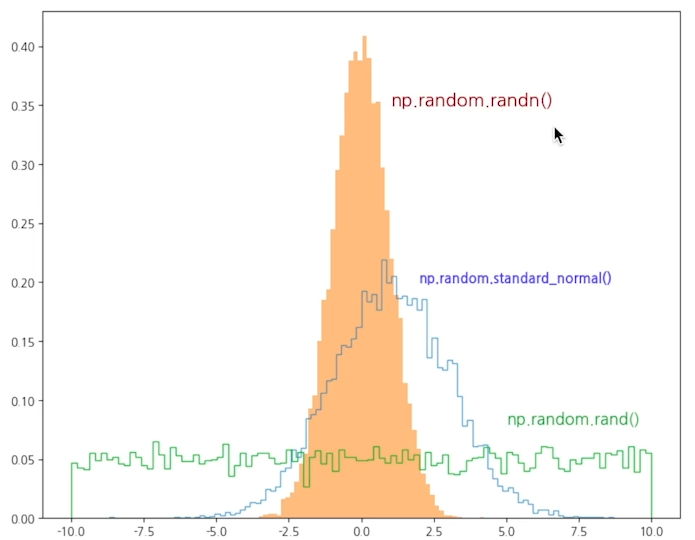
플롯 스타일을 다양하게 연출해보자! 위의 사진처럼 플롯 데이터에 텍스트를 삽입할 수 있다.plt.text(x위치,y위치,fontdict)그래프의 적절한 위치에 텍스트를 삽입하도록한다. font는 딕셔너리 형태로 저장 후 plt.text의 fontdict= 인자에 넣어주
30.[33일차]matplotlib plot의 종류 - Subplots
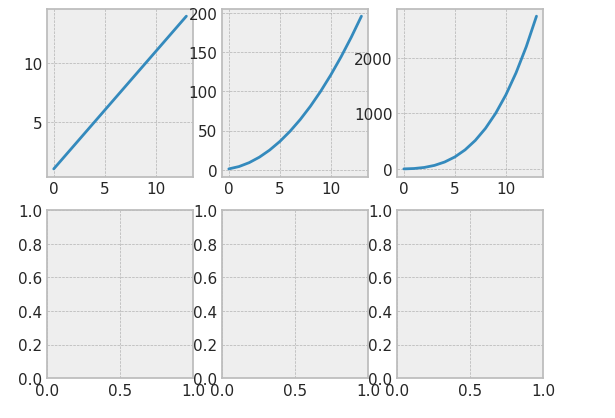
하나의 화면 안에 여러 플롯을 넣을 수 있다.인자값 : fig, axesfig, axes를 plt.subplots()의 인자로 넣은 뒤axes행,열.plot명령어를 입력해 각 subplot에 원하는 플롯을 넣을 수 있다.2행 3열의 공간에 플롯 6개를 한번에 표현해보자
31.[33일차]seaborn 소개
seaborn은 Python에서 통계 그래픽을 만들기 위한 라이브러리이다.seaborn은 matplotlib을 기반으로 하며 pandas 데이터 구조와 밀접하게 통합된다.pandas DataFrame과 직관적으로 연계되기 때문에 쉽고 빠르게 데이터 시각화가 가능하다.s
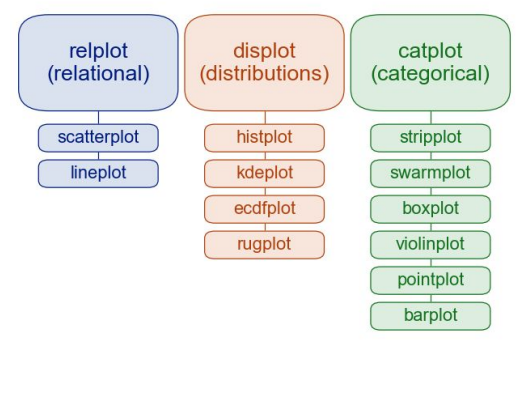
32.[33일차]seaborn plot 종류 - Relplot (Relational)
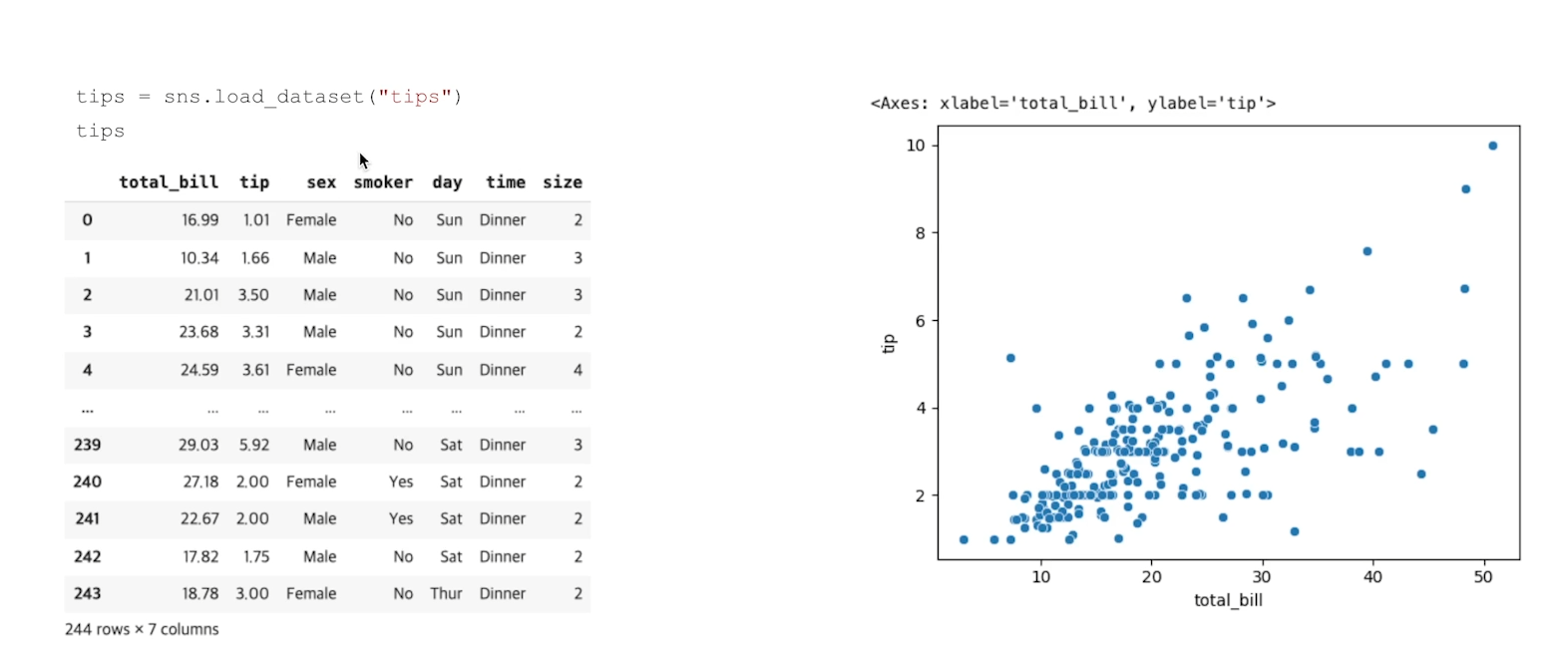
Relplot은 데이터 세트의 변수가 어떻게 연관되어 있는지, 그리고 이러한 관계가 다른 변수에 어떻게 의존하는지 이해하는데 도움을 주는 시각화가 가능하다.Relplot에서 사용 가능한 플롯은 scatter plot(산점도)과 line plot(선형)이 있다.색상, 크
33.[33일차]seaborn plot 종류 - Displot (Distributions)
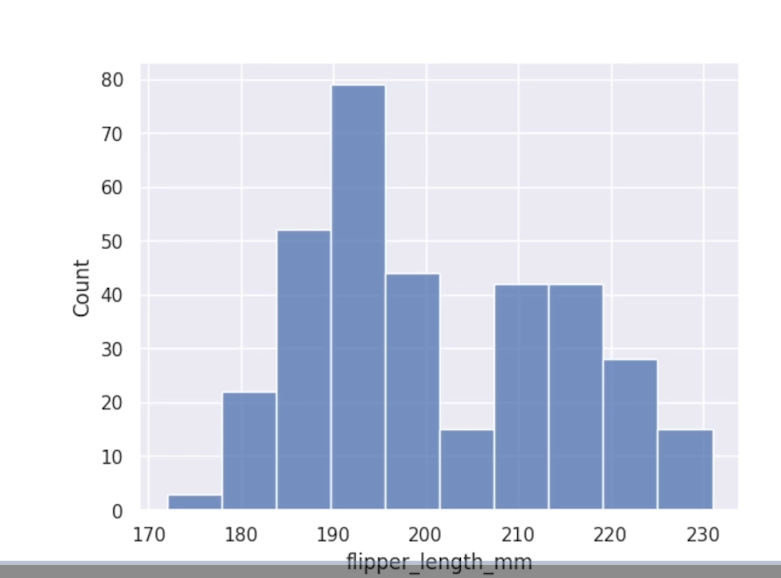
변수 하나 혹은 두 개의 분포를 나타낼 때 displot에 포함된 여러 플롯들을 사용하면 아주 효과적이다.기본적으로 히스토그램이 많이 사용된다. hue= 인자를 통해 추가 변수를 히스토그램에 추가할 수 있다.hue="species" species컬럼 은 3가지의 값이
34.[33일차]seaborn plot 종류 -조인트 플롯,pair plot
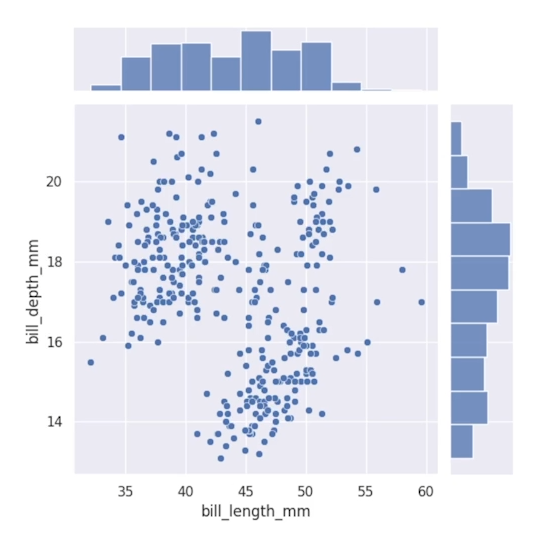
두개의 변수간 분포 + 변수의 분포를 동시에 보여줌기본적으로 산점도+히스토그램 형태를 보여준다.이때 kind=’kde’를 해주면 등고선을 그려줌hue= 를 통해 species컬럼의 값을 나눠줬다. 각 변수들간의 관계를 시각화 할 수 있다.특히, 고려해야할 변수들이 많은
35.[33일차]seaborn plot 종류 - Catplot (Categorical)_strip plot
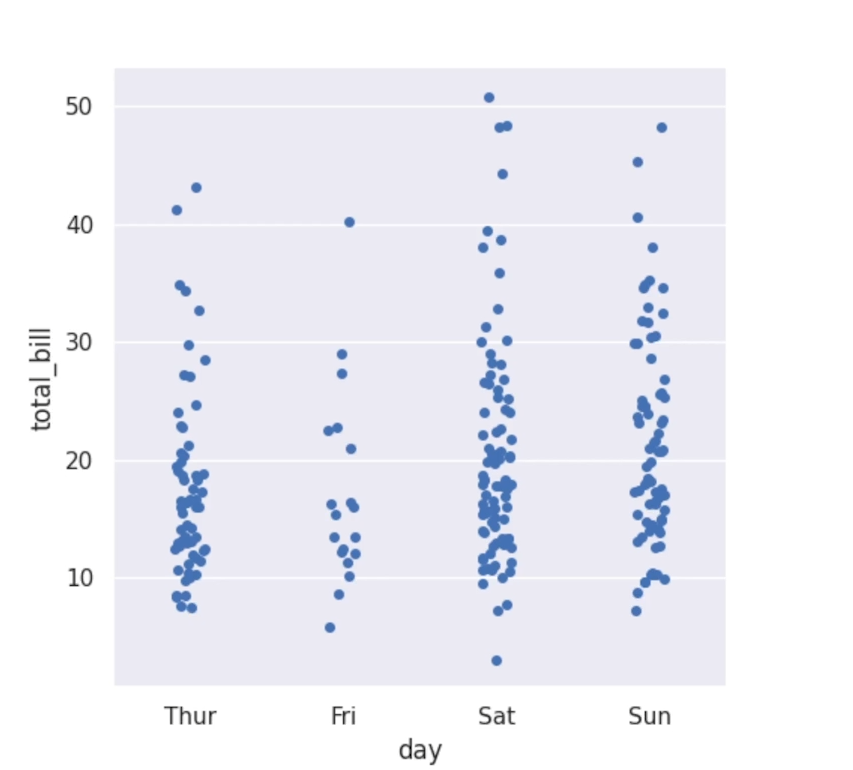
relplot() 에서 다루고자 하는 변수가 categorical(혹은 이산형 : 일정한 원소값을 같는. 요일같이)데이터인 경우 산점도나 선형플롯대신 catplot()을 사용하는 것이 더 효과적이다.catplot() 에서 사용 가능한 플롯들은 크게 3가지로 나뉜다.범주
36.[33일차]seaborn plot 종류 - Catplot (Categorical)_boxplot
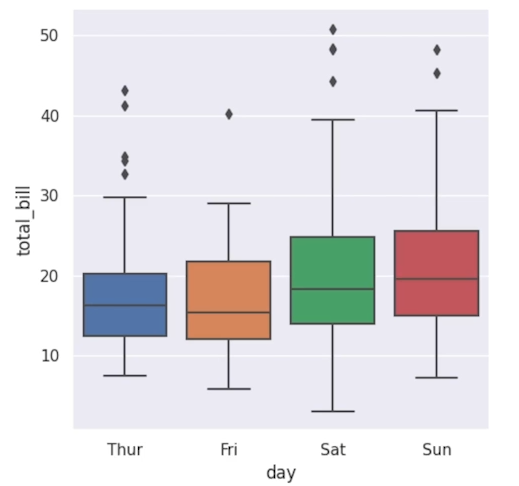
박스플롯을 만들어준다.데이터 세트 크기가 커짐에 따라 범주형 산점도는 각 범주 내의 값 분포에 대해 제공할 수 있는 정보가 제한된다. hue를 추가 가능하며 각 수준에 대한 상자는 더 좁아지고 범주형 축을 따라 이동하게된다. 박스플롯에서 분위수를 좀 더 자세하게 표시해
37.[33일차]seaborn plot 종류 - Catplot (Categorical)_barplot
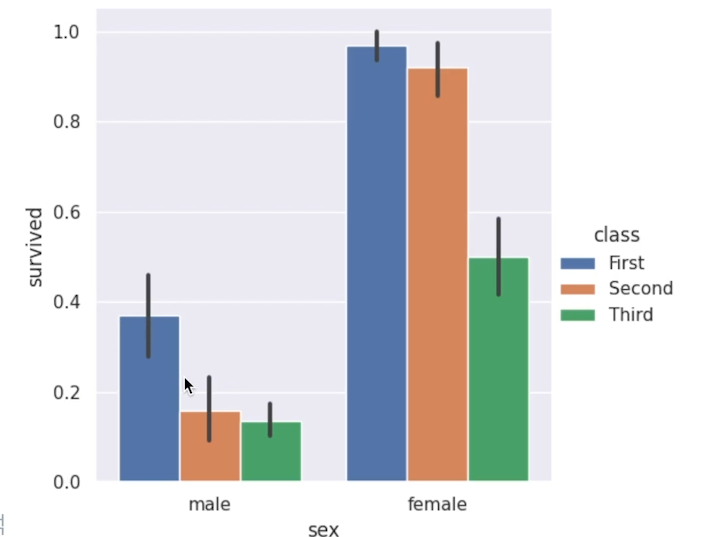
제일 많이 사용할 막대그래프도 쓸 수 있다!catplot()의 kind= 인자에 ‘bar’를 넣으면 됨.hue 를 넣어 다른 변수도 넣어줬다. 여기서 막대기가 하나 생기는데 이건자동으로 생성되는 95%신뢰구간이다.이걸 보고 95%의 신뢰구간이 짧을 수록 더 유의미하다고
38.[33일차]seaborn plot 종류 - Catplot (Categorical)_Pointplot
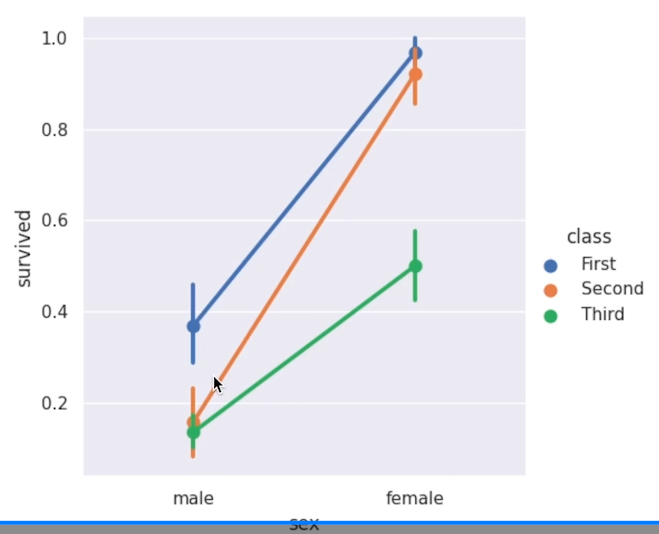
pointplot은 Catrgorical변수에 따라 다른 변수가 어떻게 변화하는지를 효과적으로 나타낸다.이때 점 추정치 중심으로 95% 신뢰구간이 표현 된다.catplot 에서 kind= 인자에 ‘point’를 넣어서 사용! 이때, marker= 인자와 linestyl
39.시각화 꿀팁

시각화는 센스가 제일 중요!남들이 어떻게 시각화를 했는지 많이보는것이 좋다고 한다.
40.[34일]데이터 모델링이란?

주어진 데이터에서 사용하고자 하는 x(feature), 알고싶은 값 y(label)가 있을 때!y=f(x)라는 함수를 통해서 x와 관계를 설명할 수 있다면 일상생활에서 아주 유용하게 사용할 수 있을 것이다.이때 y와 x의 관계를 효과적으로 설명하는 f() 함수를 만드는
41.[34일]데이터 모델링 - Bayes theorem의 관점

Bayes theorem : 조건부 확률을 계산하는 방법이다.조건부 확률 : 어떤 사건이 일어났다는 ‘전제 하에’ 다른 사건이 일어날 확률.e.g. 두 사건 A,B가 있을 때, 사건 A가 일어났을 때 B가 일어날 확률은?식으로 보면 이렇다. A와 B가 동시에 일어날 확
42.[34일차]데이터 모델링 과정

데이터를 전처리 및 분석한다.데이터를 training set, test set으로 나눈다.training set에 대해서 사용할 모델을 학습시킨다.(model.fit(training_set))test set에 대해서 학습된 모델의 예측값을 통해 모델의 성능을 평가한다.
43.[34일차]데이터 모델링 - 선형회귀(Linear Regression)
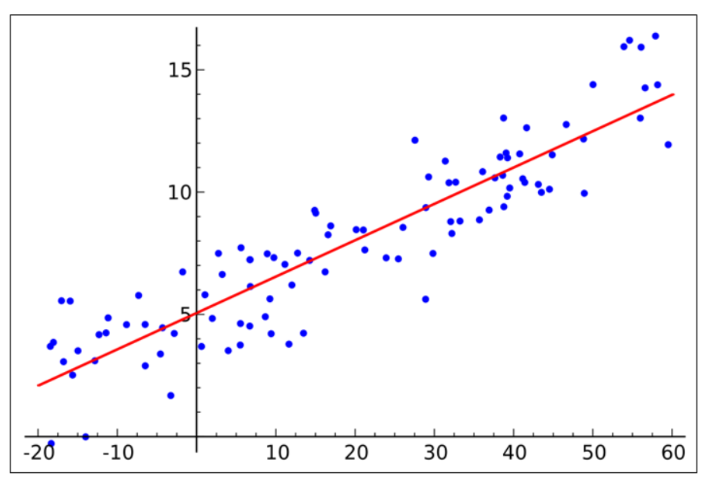
y=f(x)+ε의 형태로 입력 변수 x와 출력 변수 y 사이의 선형 상관 관계를 모델링하는 분석 기법이다.e.g. 자동차가 이동한다고 했을 때시간이 지남에 따라 자동차가 얼마나 움직였는지 알고 싶을 때 선형 회귀를 사용할 수 있다.자동차가 움직이는 각 시간, 위치를 기
44.[34일]데이터 모델링 - Gradient descent
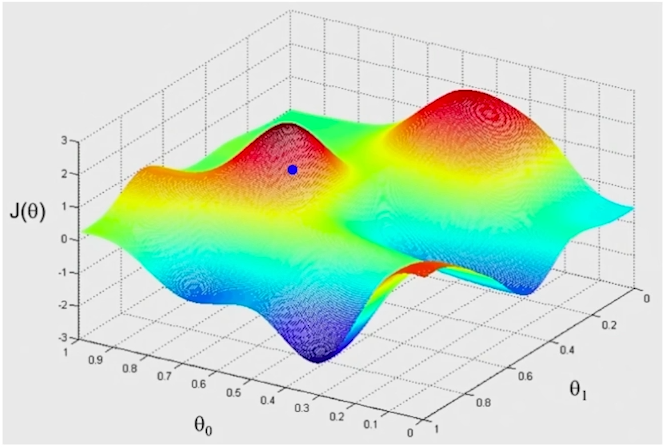
변수가 많아지거나 cost function이 복잡해지는 경우, 최소 제곱법을 통해서 한번에 loss가 최소인 parameter를 추정하기 어렵다.이러한 경우, 각 parameter에 대해서 비용함수(cost function)를 편미분한 값(경사(gradient))을
45.[34일]Ridge, Lasso
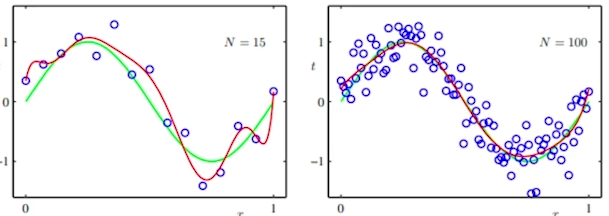
데이터 모델링을 하는 경우 overfiting(과적합) 되는 경우가 많다.학습데이터에 대해서 과하게 fiting되는 경우를 의미‘과하게 fiting’ 된다는 의미는 무엇일까?그 의미를 알기 위해서는 일반화에 대해서 알아야 된다.학습할 때와 추론할 때의 성능 차이가 많이
46.[34일차]로지스틱 회귀, SVM
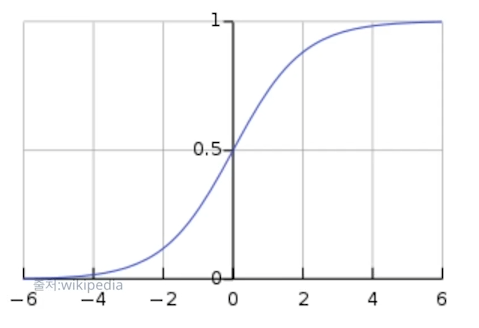
데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측한 뒤 그 확률에 따라서 가능성이 특정 기준치(threshold) 이상인 경우 해당 클래스로 분류해 주는 지도학습 알고리즘이다.Linear regression의 output y값에’Sigmoid functi
47.[34일차]Random Forest
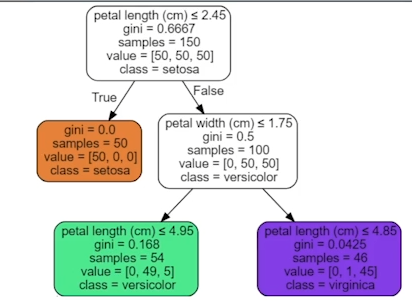
이번 글에서는 \*\*Random Forest\*\*에 대해서 알아보려고 한다.그전에! Decision Tree에 대해 간단하게 알아보자.x를 기준삼아, ‘해당 기준을 만족/불만족시 y값이 ~값일 것이다.’라는 조건(x)-결과(y)를 나무처럼 발전시킨 것을 말한다. C
48.[프로그래머스]주문량이 많은 아이스크림들 조회하기

https://school.programmers.co.kr/learn/courses/30/lessons/133027음.. 이번 문제는 cte를 이용해서 너무 쉽게 풀었다...다른 분들의 풀이를 보면 ORDER BY 절에서 SUM 구문을 사용하셨더라이게 좀 더
49.[35일차]데이터 모델링 - Naive Bayes

주어진 정보를 사용하여 어떤 일이 얼마나 발생할지 예측하는 방법e.g. 사람들이 강아지를 얼마나 좋아하는지를 알기 위해 질문을 해보자”강아지를 좋아하는 친구는 얼마나 많아?”, “강아지를 싫어하는 친구는 몇명이야?”이러한 의견을 모아서 전체적인 판단을 내릴 수 있듯.\
50.[35일차]모델링 평가 방법(Evaluation)
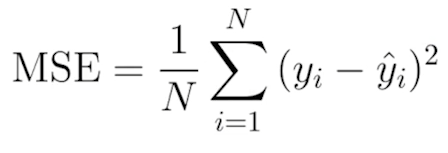
모델을 제대로 평가하는 metric(지표)를 사용해야 주어진 데이터에서가장 효과적인 모델을 사용할 수 있다.모델링 평가방법에 대해서 알아보자오차(틀린값)의 제곱을 평균으로 나눈 값.즉 평균으로 나눈 값이 0에 가까울 수록 좋은 성능이라고 볼 수 있다. 식을 보면 제곱의
51.[35일차]데이터 모델링 - PCA
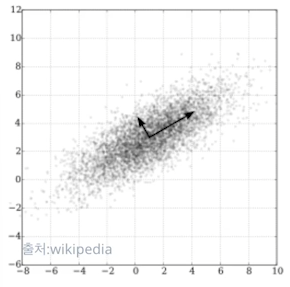
PCA는 고차원의(feature가 많은) x에 대해서 주어진 x들의 분포를 가장 잘 설명하는x축, y축을 찾아내는 기술이다. 업로드중..데이터가 퍼져있는 사진이다.분포가 많은 가로부분을 x축, 그 직교를 이루는 부분을 y축으로 한다.이렇게 새로운 x축과 y축을 찾아낸
52.[35일차]Feature Analysis
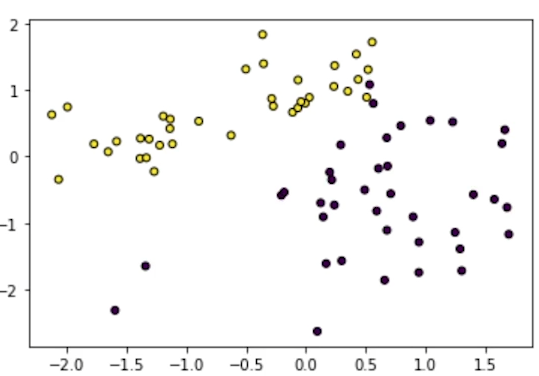
데이터를 설명하는 feature x와 알아보고자 하는 label y가 있을 때, 어떠한 feature가 y를 설명하는데에 있어 중요한 feature인지 아는 것 또한 매우 중요하다. 지금 까지 배운 데이터 모델링 Logistic regression이나 linear
53.[35일차]상관관계 분석
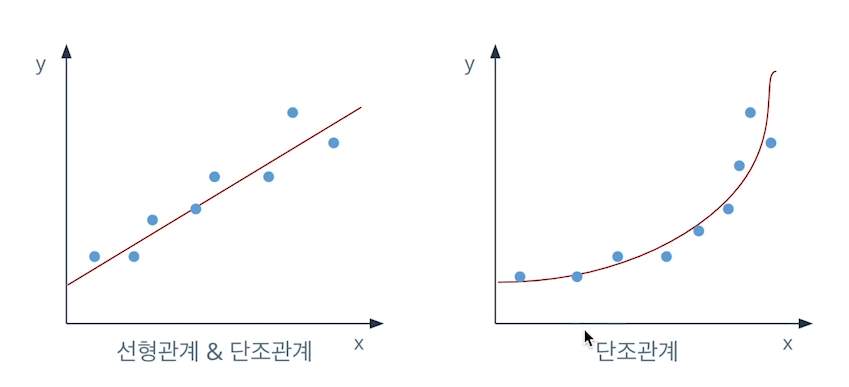
feature 분석을 하면서 각 상관관계를 분석하는 것 또한 중요할 수 있다.이번 글에서는 각 feature들과 label간의 상관관계 분석을 통해 feature의 중요도를 알아보자.상관관계란?통계적 변인과 다른 여러 통계적 변인들이 하나가 변하면 같이 변하는 함수관계
54.[35일]7주차 요약

7주차 복습은 아래 키워드를 바탕으로 진행 고고~데이터 분석 프로세스문제 정의 - 데이터 수집 - 데이터 전처리 - 데이터 분석 - 리포팅 피드백정규화와 데이터 스케일링정규화(normalization): min-max normalization, Z-score norma