[32일차]ANOVA

AVOVA(analysis of variance, 분산분석)

AVOVA : n개의 집단을 비교하는 통계적 분석(n>2)

• n>2인 경우 n개의 집단에서 t 검정을 하는 경우 문제 발생

  • e.g. n개의 집단에서 한번이라도 type 1 error가 발생할 확률 = 1-0.95^n>0.05
    즉, type 1 error의 누적을 해결하기 위해 ANOVA 사용

• 분산분석은 사용하기 전 3가를 만족해야 된다. : 정규성, 독립성, 등분산성

  • 정규성 : 모든 데이터가 정규분포를 따르는 모집단으로부터 추출됨
    정규분포를 따르지 않는 것으로 보이는 경우 Log 변환 등의 전처리가 필요(종모양으로 만듦)
  • 독립성 : 데이터가 모집단으로 부터 독립적으로 추출되어야 됨.
  • 등분산성 : 모든 데이터는 분산이 동일한 모집단들로 부터 추출됨
    (보통은 가장 큰 분산과 작은 분산의 비가 4:1정도를 넘지 않으면 ANOVA를 적용해도 됀찮은 것으로 봄.)

  

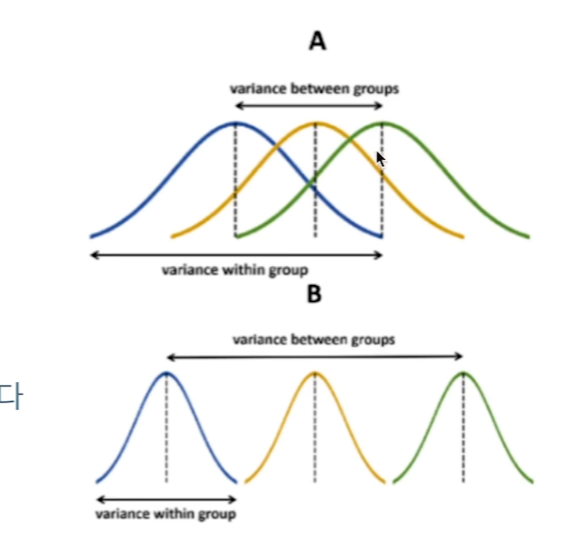
우리가 가정하는 집단이 3개라고 했을 때,
A같은 경우에는 겹치는 부분이 많이 때문에 같은 모집단으로 볼 수 있다.

B는 다른 모집단으로 보았다 하고 분산 분석을 할 수 있다.

일원 분산분석(one - way ANOVA):

집단의 종류(독립변수)가 하나이고 집단들이 가지는 평균값(종속 변수)이 하나인 경우 그 집단간 모평균의 차이의 여부를 검증하는 방법